112 Stellar Radii (Lesson)
Janice Hester

An image of the Sun taken in visible light shows the Sun's photosphere, which is a thin outer layer of the star where most of the light leaving the star is generated. The photosphere is the closest thing that a star has to a surface, and when we talk about the size of a star, we are talking about the extent of its photosphere.
Astronomy 2e on OpenStax discusses several ways that we can measure the size of a star (18.3 Diameters of Stars). Of the ways discussed, one is foundational to understanding stars. The star's size, surface temperature, and luminosity are all linked to each other. If we measure a star's luminosity and its surface temperature (using its color), we can estimate the star's size. The connection between these properties also helps explain why some stars become giants or super giants towards the end of their "life" as stars.
A star's luminosity is the rate at which light leaves the star, streaming away from the photosphere in all directions. Larger stars tend to be more luminous, because they have a larger photospheres generating light. But the intensity of light leaving the star's surface is also important. If the light leaving a star's surface is more intense (if more energy is generated by each square meter of the star's surface), then a smaller star might be more luminous. For real stars, both stellar sizes and surface intensities vary, and the most luminous stars have a mix of sizes and surface intensities.
Stellar Size and Luminosity

| Star | Luminosity [latex]\left(L_{\odot}\right)[/latex] | B-V Color | r [latex]\left(r_{\odot}\right)[/latex] |
| Sun | 1 | 0.65 | 1 |
| Sirius | 25.4 | 0.00 | 1.7 |
| Betelgeuse | [latex]\approx[/latex]100,000 | 1.85 | 764 |
| Rigel | 120,000 | -0.03 | 78.9 |
The table above shows the luminosity, color, and size for the Sun and a few bright stars that are visible in the night sky. (Betelgeuse and Rigel are both in the constellation Orion; Sirius - the Dog Star - is in Canis Major.) In the table, the luminosity is given in terms of the Sun's luminosity; the symbol for which is [latex]L_{\odot}[/latex]. Sirius has a luminosity that is 25.4 times that of the Sun (Sirius's luminosity is 25.4 [latex]L_{\odot}[/latex]). Rigel has a luminosity that is 120,000 times the Sun's (120,000 [latex]L_{\odot}[/latex]). Similarly, the radius is given in terms of the Sun's radius ([latex]r_\odot[/latex]).
Compare Sirius and Rigel. Rigel is a giant star with a luminosity that is about 120,000 times the Sun's and 4,700 times Sirius's. The main reason that Rigel is much more luminous than Sirius is Rigel's size. While Sirius's radius is a modest 1.7 times the Sun's; Rigel's radius is almost 80 times larger than the Sun's and about 46 times larger than Sirius's.
To understand how a radius that is 46 times larger leads to a star that is thousands of times more luminous, we need to think closely about what we mean by a star's size. We can compare Rigel to Sirius by comparing the stars' radii, but we can also compare their surface areas and their volumes. In every case, Rigel is larger than Sirius, but the ratio between the stars' sizes depends on which measure of size we use. Rigel's radius is about 46 times larger than Sirius's, but because surface area is proportional to radius squared ([latex]\text{SA}=4\pi r^2[/latex]), Rigel has about 2,100 times as much surface area. Volume is proportional to radius cubed ([latex]V=\frac{4}{3}\pi r^3[/latex]), so Rigel's volume is almost 100,000 times Sirius's.
Now compare Betelgeuse and Rigel. The two stars have similar luminosities, but Betelgeuse's radius is almost 10 times larger than Rigel's.
Betelgeuse is a larger star than Rigel, but its luminosity is slightly lower than Rigel's. This is possible because the intensity of light leaving the surface of Rigel is higher than that leaving the surface of Betelgeuse.
Surface Temperature
The light leaving a star's photosphere is mostly thermal radiation (plus some absorption and emission lines from the star's atmosphere). We could see in a star's spectra (below) that the continuum (the general shape of the spectrum) follows a black body spectrum (also called a Planck spectrum).
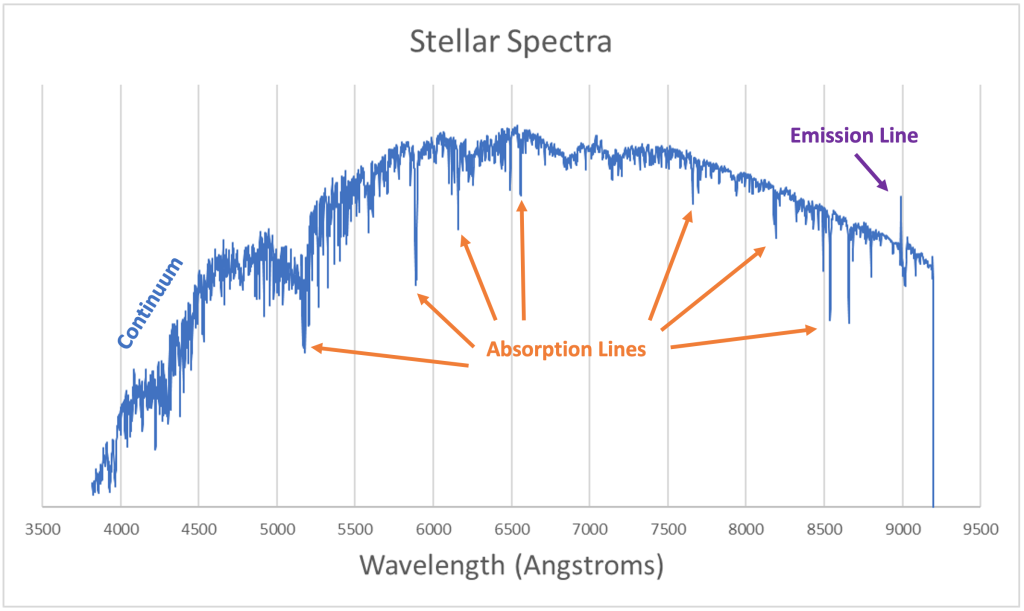
Increasing the temperature of an object increases the brightness of its thermal radiation. More specifically, the intensity of the thermal radiation (light energy per unit surface area caused by thermal motions) leaving a surface is proportional to [latex]T^4[/latex]. This is called the Stefan-Boltzmann law, which was introduced in 5.2 The Electromagnetic Spectrum in Astronomy 2e on OpenStax.
[latex]f=\sigma T^4[/latex]
Where [latex]f[/latex] is the energy flux, or the rate at which energy is radiated away from each square meter of the object's surface (I've been calling this the intensity), [latex]T[/latex] is the object's surface temperature, and [latex]\sigma[/latex] is a constant called the Stefan-Boltzmann constant.

The flux is very dependent on temperature. Because temperature is raised to the fourth power ([latex]T^4[/latex]), doubling the temperature will increase the thermal flux by a factor of 16 ([latex]2^4=16[/latex]). This means that if two stars have the same size, then a star with a surface temperature of 4,000 K will have a luminosity that is 16 times greater than a star with a surface temperature of 2,000K. Doubling the thermal flux from an object only requires an increase in temperature of about 20% ([latex]\sqrt[4]{2}\approx1.19[/latex]).
Estimating a Star's Size
A star's luminosity depends on both its size and its surface temperature. Sirius is brighter than the Sun because it is both larger and hotter than the Sun. Betelgeuse has a lower surface temperature than the Sun (it has a redder B-V color), but is much brighter than the Sun because it is much larger than the Sun (its surface area is about 580,000 times larger). Rigel, which is a giant star, but still smaller than Betelgeuse, is brighter than Betelgeuse because it has a higher surface temperature (a bluer B-V color).
If we measure the luminosity and color of a star, we can use this reasoning in reverse to compare the sizes of stars.
As an equation...
[latex]L\left(L_\odot\right)=\left(1.862\times10^{-33}L_\odot m^{-2} K^{-4}\right)T^4\left(K^4\right)r^2\left(m^2\right)[/latex]
In this equation [latex]L[/latex] is the star’s luminosity in multiples of the Sun’s luminosity ([latex]L_\odot[/latex]), [latex]T[/latex] is the star’s surface temperature in Kelvin, and [latex]r[/latex] is the radius of the star in meters. This equation assumes that the star's entire surface radiates like a black body, which is not quite correct, but close enough.
We can use this equation to estimate the size of a star by
- Measuring the luminosity of the star
- Using the star's color to estimate its surface temperature
- Solving the equation above for radius
