We can use the properties of thermal spectra to measure the temperatures of distant objects. For example, the surface temperatures of stars and planets are measured using their spectra. To see how we can do this, examine the thermal spectra for four different temperatures shown below.  Notice that all of the graphed spectra have a similar shape.  Starting from shorter (bluer) wavelengths and moving towards longer wavelengths, each spectrum rises quickly up to a peak and then tapers off towards longer (redder) wavelengths.  This characteristic shape is called the Planck spectrum, and the peak of the Planck spectrum is determined by the object’s temperature.  The spectra of hotter objects peak at shorter wavelengths. By measuring the wavelength of this peak, we can determine the temperature of the spectrum’s source (the object that emitted the light).

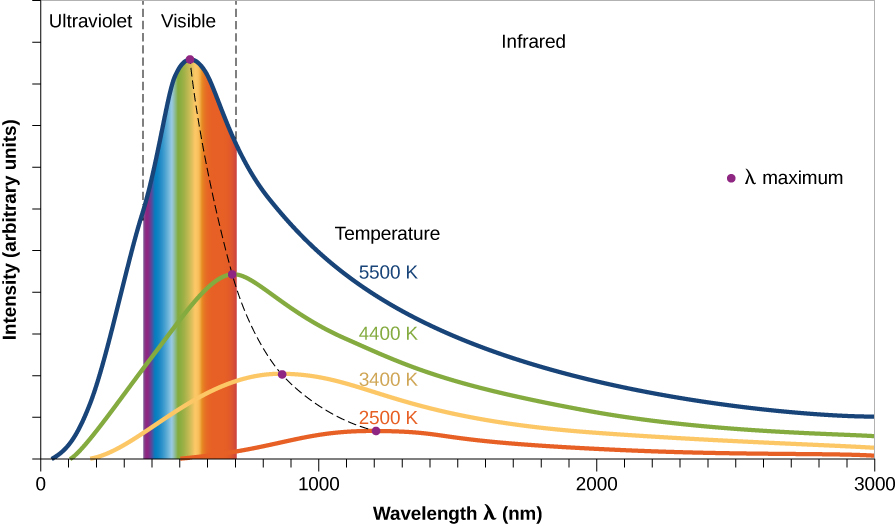
A Planck spectrum is also called a black-body spectrum. In physics, a black-body is a hypothetical object that absorbs all of the light that falls on it. Such an object doesn’t exist, but a black-body spectrum is an important idea in physics and astronomy.

When we talk about a thermal spectrum (or a Planck spectrum or a black-body spectrum), we are talking about the light that an object gives off because of the thermal motions of the atoms and molecules that it is made up of (called its thermal radiation). Any light that bounces off of an object (i.e., that is reflected from the object) is not part of its thermal spectrum. Any sufficiently dense object (the surface of a star, the Earth, a meerkat, a pond, or you) emits thermal radiation with the characteristic shape of a Planck spectrum.

Wien’s Law

The mathematical relationship between the peak of a thermal spectrum and the temperature of the object’s source is called Wien’s law.  Wien’s law is used to calculate the temperature of an object after measuring the peak of its thermal spectrum.

[latex]\lambda_{peak}=\frac{2900 \mu mK}{T}[/latex]

The temperature of the source and the wavelength at which the spectrum peaks are inversely proportional.  As the temperature increases, the peak shifts towards lower wavelengths.  More specifically, the peak wavelength decreases by whatever factor the the temperature increases by.  For example if the temperature increases by a factor of two (doubles), the wavelength of the peak decreases by a factor of two (halves), and vice versa, halving the temperature would double the peak’s wavelength.

Stefan-Boltzmann Law

As the temperature of an object increases, the intensity of the thermal radiation it emits also increases (it gets brighter).  The relationship between the intensity of the thermal radiation leaving an object’s surface (the light energy per square meter of the object’s surface area) is given by the Stefan-Boltzmann law.

[latex]f=\sigma T^4[/latex]

In this formula, [latex]\sigma[/latex] is a constant called the Stefan-Boltzmann constant.

When an object gets hotter, it gets much brighter; the intensity is proportional to temperature raised to the fourth power ([latex]T^4[/latex]).  Doubling the temperature doesn’t just double, or even quadruple, the intensity of the object’s thermal radiation… it increases the intensity by a factor of 16.

Concept Check