1 Chapter 1: Statistical Thinking, Research Methods and Data

Alisa Beyer

Types of Data and How to Collect Them

In order to use statistics, we need data to analyze. Data come in an amazingly diverse range of formats, and each type gives us a unique type of information. In virtually any form, data represent the measured value of variables. A variable is simply a characteristic or feature of the thing we are interested in understanding. Let’s imagine we want to conduct a study to measure the stress level of students who are taking PSY 230. We will administer the survey during the first week of the course. One question we will ask is, “How stressed have you been in the last 2 weeks, on a scale of 0 to 10, with 0 being not at all stressed and 10 being as stressed as possible?”

  • Variable is a condition or characteristic that can take on different values. In our example, the variable was stress, which can take on any value between 0 and 10. Height is a variable. Social class is a variable. One’s score on a creativity test is a variable. The number of people absent from work on a given day is a variable. In psychology, we are interested in people, so we might get a group of people together and measure their levels of anxiety (a variable) or their physical health (another variable). You get the point. Pretty much anything we can count or measure can be a variable.
    • Once we have data on different variables, we can use statistics to understand if and how they are related. 
  • A value is just a number, such as 4, – 81, or 367.12. A value can also be a category (word), such as male or female, or a psychological diagnosis (major depressive disorder, post-traumatic stress disorder, schizophrenia).
    • We will learn more about values and types of data a little later in this chapter.
  • Each person studied has a particular score that is his or her value on the variable. As we’ve said, your score on the stress variable might have a value of 6. Another student’s score might have a value of 8.

We also need to understand the nature of our data: what they represent and where they came from.  We will briefly review some keys to understanding statistical studies.

Tips to understanding statistical studies

Here are a few key considerations for evaluating studies using statistics.

  1. Know the basic components of a statistical investigation.
  2. Know the sample.  Identify if using a representative sample.
  3. Identify the sample size. Evaluate if using a large enough sample.
  4. Understand and evaluate the study design.
  5. Identify type of data working with.
  6. Understand the statistics used.
  7. Evaluate conclusions made from statistical findings.
The basic components to a statistical investigation
  • Planning the study: Start by asking a testable research question and deciding how to collect data. For example, how long was the study period of the study? How many people were recruited for the study, how were they recruited, and from where? How old were they? What other variables were recorded about the individuals, such as smoking habits, on the comprehensive lifestyle questionnaires? 
  • Examining the data: What are appropriate ways to examine the data? What graphs are relevant, and what do they reveal? What descriptive statistics can be calculated to summarize relevant aspects of the data, and what do they reveal? What patterns do you see in the data? Are there any individual observations that deviate from the overall pattern, and what do they reveal? 
  • Inferring from the data: What are valid statistical methods for drawing inferences “beyond” the data you collected? Is a 10%–15% reduction in risk of death something that can happen just by chance?
  • Drawing conclusions: Based on what you learned from your data, what conclusions can you draw? Who do you think these conclusions apply to? Can you draw a cause-and-effect conclusion about your treatment? (note: we are about to learn more about the study design needed for this)

Notice that the numerical analysis (“crunching numbers” on the computer) comprises only a small part of the overall statistical investigation. In this module, you will see how we can answer some of these questions and what questions you should be asking about any statistical investigation you read about. In the end, statistics provides us a way to give a very objective “yes” or “no” answer to the question, “is this treatment or intervention effective and, if so, how effective is it?” Nearly all statistical techniques boil down to answering these questions. Statistics is all about helping make correct and reliable decisions in our chosen field of study. But even if you never plan on conducting research or pursuing a career where you have to use statistics, the material in this course will help you in your daily life. In today’s world of instant gratification, information overload, and the 24-hour news cycle, statistics are thrown at us nonstop. Soon, you will be able to determine if the person or group providing these statistics is being honest or manipulating the data to suit their ideas.

Let’s learn a little bit more about what is needed to know to better understand statistics.

Who are your participants? Who is your population?

Research in psychology typically begins with a general question about a specific group (or groups) of individuals or animals. For example, a researcher might want to know how many homeless people live on the streets of Phoenix. Or a researcher might want to know how often married people have sex, as reported by partners separately. In the first example, the researcher is interested in the group of homeless people. In the second example, the researcher may study heterosexual couples and compare the group of men with the group of women. In statistics, we call the entire group that a researcher wishes to study a population. As you can well imagine, a population can be quite large; for example, any student enrolled in college. A researcher might be more specific, limiting the population for a study to college students who have successfully completed a statistics course and who live in the United States.

Populations can obviously vary in size from extremely large to very small, depending on how the researcher defines the population. The population being studied should always be identified by the researcher. In addition, the population can include more than people and animals. A population could be corporations, parts produced in a factory, or anything else a researcher wants to study. Because populations tend to be very large it usually is impossible for a researcher to examine every individual in the population of interest. It is typically not feasible to collect data from an entire population. Therefore, researchers typically select a smaller, more manageable group from the population and limit their studies to the individuals in the selected group. A smaller more manageable group, known as a sample, is used to measure populations.

The participants in the research are the sample, and the larger group the sample represents is the population.  In statistical terms, a set of individuals selected from a population is called a sample . A sample is intended to be representative of its population, and a sample should always be identified in terms of the population from which it was selected. As with populations, samples can vary in size. For example, one study might examine a sample of only 10 autistic children, and another study might use a sample of more than 10,000 people who take specific cholesterol medication. The sample is intended to represent the population in a research study.

When describing data it is necessary to distinguish whether the data come from a population or a sample.

  • If data describe a sample it is called a statistic.
  • If data describe a population it is called a parameter.

If I had given a statistical attitudes survey to the class, the class would be my sample.  I might be interested in all students taking a statistics class for the first time, generalizing my findings to all statistics students would be applying information from my sample to a population.  While it might be convenient for me to ask my class, does my class best represent all students taking statistics? I would need to carefully consider selecting the best sample for a population or critically think about the limits for generalizing my findings to a population. While our results would be most accurate if we could study the entire population rather than a sample from it, in most research situations this is not practical. Moreover, research usually is to be able to make generalizations or predictions about events beyond your reach. Additionally, sampling is an important concept to consider with the big picture of understanding statistics.

Imagine that we wanted to see if statistics anxiety was related to procrastination. We could measure everyone’s levels of statistics anxiety and procrastination and observe how strongly they were related to each other. This would, however, be prohibitively expensive. A more convenient way is to select a number of individuals randomly from the population and find the relationship between their statistics anxiety and procrastination levels. We could then generalize the findings from this sample to the population. We use statistics, more specifically inferential statistics, to help us generalize from a particular sample to the whole population. Understanding the relationship between populations and their samples is the first vital concept to grasp in this course. Remember that the research started with a general question about the population but to answer the question, a researcher studies a sample and then generalizes the results from the sample to the population.

As we move into further concepts in statistics, we will see that how you get your participants (sampling) and sample size are important.  The general rule is to get a large enough sample size and have the sample be a good representation of your population.

Representative Sample

Because we are using samples to generalize to the larger population it is important, vital, that the samples look like the population they came from. When the sample closely matches the population from which it was selected we call this a representative sample. An unrepresentative (biased) sample is a subset of the population that does not have the characteristics typical of the target population.

Random Sampling

Usually, the ideal method of picking out a sample to study is called random selection or sampling. The researcher starts with a complete list of the population and randomly selects some of them to study. . Random sampling is considered a fair way of selecting a sample from a given population since every member is given equal opportunities of being selected. This process also helps to ensure that the sample selected is more likely to be representative of the larger population. Theoretically, the only thing that can compromise its representativeness is luck. If the sample is not representative of the population, the random variation is called sampling error.

 

Example #1: You have been hired by the National Election Commission to examine how the American people feel about the fairness of the voting procedures in the U.S. Who will you ask?
It is not practical to ask every single American how he or she feels about the fairness of the voting procedures. Instead, we query a relatively small number of Americans, and draw inferences about the entire country from their responses. The Americans actually queried constitute our sample of the larger population of all Americans.
A sample is typically a small subset of the population. In the case of voting attitudes, we would sample a few thousand Americans drawn from the hundreds of millions that make up the country. In choosing a sample, it is therefore crucial that it not over-represent one kind of citizen at the expense of others. For example, something would be wrong with our sample if it happened to be made up entirely of Florida residents. If the sample held only Floridians, it could not be used to infer the attitudes of other Americans. The same problem would arise if the sample were comprised only of Republicans. Inferences from statistics are based on the assumption that sampling is representative of the population. If the sample is not representative, then the possibility of sampling bias occurs. Sampling bias means that our conclusions apply only to our sample and are not generalizable to the full population.

Example #2: We are interested in examining how many math classes have been taken on average by current graduating seniors at American colleges and universities during their four years in school.
Whereas our population in the last example included all US citizens, now it involves just the graduating seniors throughout the country. This is still a large set since there are thousands of colleges and universities, each enrolling many students. (New York University, for example, enrolls 48,000 students.) It would be prohibitively costly to examine the transcript of every college senior. We therefore take a sample of college seniors and then make inferences to the entire population based on what we find. To make the sample, we might first choose some public and private colleges and universities across the United States. Then we might sample 50 students from each of these institutions. Suppose that the average number of math classes taken by the people in our sample were 3.2. Then we might speculate that 3.2 approximates the number we would find if we had the resources to examine every senior in the entire population. But we must be careful about the possibility that our sample is non-representative of the population. Perhaps we chose an overabundance of math majors, or chose too many technical institutions that have heavy math requirements. Such bad sampling makes our sample unrepresentative of the population of all seniors.
To solidify your understanding of sampling bias, consider the following example. Try to identify the population and the sample, and then reflect on whether the sample is likely to yield the information desired.
Example #3: A substitute teacher wants to know how students in the class did on their last test. The teacher asks the 10 students sitting in the front row to state their latest test score. He concludes from their report that the class did extremely well. What is the sample? What is the population? Can you identify any problems with choosing the sample in the way that the teacher did?
In Example #3, the population consists of all students in the class. The sample is made up of just the 10 students sitting in the front row. The sample is not likely to be representative of the population. Those who sit in the front row tend to be more interested in the class and tend to perform higher on tests. Hence, the sample may perform at a higher level than the population.
Example #4: A coach is interested in how many cartwheels the average college freshmen at his university can do. Eight volunteers from the freshman class step forward. After observing their performance, the coach concludes that college freshmen can do an average of 16 cartwheels in a row without stopping.
In Example #4, the population is the class of all freshmen at the coach’s university. The sample is composed of the 8 volunteers. The sample is poorly chosen because volunteers are more likely to be able to do cartwheels than the average freshman; people who can’t do cartwheels probably did not volunteer! In the example, we are also not told of the gender of the volunteers. Were they all women, for example? That might affect the outcome, contributing to the non-representative nature of the sample (if the school is co-ed).
Simple Random Sampling

Researchers adopt a variety of sampling strategies. The most straightforward is simple random sampling. Such sampling requires every member of the population to have an equal chance of being selected into the sample. In addition, the selection of one member must be independent of the selection of every other member. That is, picking one member from the population must not increase or decrease the probability of picking any other member (relative to the others). In this sense, we can say that simple random sampling chooses a sample by pure chance. To check your understanding of simple random sampling, consider the following example.

What is the population? What is the sample? Was the sample picked by simple random sampling? Is it biased?
Example #5: A research scientist is interested in studying the experiences of twins raised together versus those raised apart. She obtains a list of twins from the National Twin Registry, and selects two subsets of individuals for her study. First, she chooses all those in the registry whose last name begins with Z. Then she turns to all those whose last name begins with B. Because there are so many names that start with B, however, our researcher decides to incorporate only every other name into her sample. Finally, she mails out a survey and compares characteristics of twins raised apart versus together.
In Example #5, the population consists of all twins recorded in the National Twin Registry. It is important that the researcher only make statistical generalizations to the twins on this list, not to all twins in the nation or world. That is, the National Twin Registry may not be representative of all twins. Even if inferences are limited to the Registry, a number of problems affect the sampling procedure we described. For instance, choosing only twins whose last names begin with Z does not give every individual an equal chance of being selected into the sample. Moreover, such a procedure risks over-representing ethnic groups with many surnames that begin with Z. There are other reasons why choosing just the Z’s may bias the sample.

Perhaps such people are more patient than average because they often find themselves at the end of the line! The same problem occurs with choosing twins whose last name begins with B. An additional problem for the B’s is that the “every-other-one” procedure disallowed adjacent names on the B part of the list from being both selected. Just this defect alone means the sample was not formed through simple random sampling.

Sample size matters

Recall that the definition of a random sample is a sample in which every member of the population has an equal chance of being selected. This means that the sampling procedure rather than the results of the procedure define what it means for a sample to be random. Random samples, especially if the sample size is small, are not necessarily representative of the entire population. For example, if a random sample of 20 subjects were taken from a population with an equal number of males and females, there would be a nontrivial probability (0.06) that 70% or more of the sample would be female. Such a sample would not be representative, although it would be drawn randomly. Only a large sample size makes it likely that our sample is close to representative of the population. For this reason, inferential statistics take into account the sample size when generalizing results from samples to populations. In later chapters, you’ll see what kinds of mathematical techniques ensure this sensitivity to sample size.

More complex sampling

Sometimes it is not feasible to build a sample using simple random sampling. To see the problem, consider the fact that both Dallas and Houston are competed to be hosts of the 2012 Olympics. Imagine that you are hired to assess whether most Texans prefer Houston to Dallas as the host, or the reverse. Given the impracticality of obtaining the opinion of every single Texan, you must construct a sample of the Texas population. But now notice how difficult it would be to proceed by simple random sampling. For example, how will you contact those individuals who don’t vote and don’t have a phone? Even among people you find in the telephone book, how can you identify those who have just relocated to California (and had no reason to inform you of their move)? What do you do about the fact that since the beginning of the study, an additional 4,212 people took up residence in the state of Texas? As you can see, it is sometimes very difficult to develop a truly random procedure. For this reason, other kinds of sampling techniques have been devised. We now discuss two of them.

Stratified Sampling

Since simple random sampling often does not ensure a representative sample, a sampling method called stratified random sampling is sometimes used to make the sample more representative of the population. This method can be used if the population has a number of distinct “strata” or groups. In stratified sampling, you first identify members of your sample who belong to each group. Then you randomly sample from each of those subgroups in such a way that the sizes of the subgroups in the sample are proportional to their sizes in the population.

Let’s take an example: Suppose you were interested in views of capital punishment at an urban university. You have the time and resources to interview 200 students. The student body is diverse with respect to age; many older people work during the day and enroll in night courses (average age is 39), while younger students generally enroll in day classes (average age of 19). It is possible that night students have different views about capital punishment than day students. If 70% of the students were day students, it makes sense to ensure that 70% of the sample consisted of day students. Thus, your sample of 200 students would consist of 140 day students and 60 night students. The proportion of day students in the sample and in the population (the entire university) would be the same. Inferences to the entire population of students at the university would therefore be more secure.
Convenience Sampling

Unfortunately, it is often impractical or impossible to study a truly random sample. Much of the time, in fact, studies are conducted with whoever is willing or available to be a research participant – this is commonly referred to as convenience sampling. At best, as noted, a researcher tries to study a sample that is not systematically unrepresentative of the population in any known way. For example, suppose a study is about a process that is likely to differ for people of different age groups. In this situation, the researcher may attempt to include people of all age groups in the study. Alternatively, the researcher would be careful to draw conclusions only about the age group studied. Remember that one of the goals of research is to make conclusions about the population from the sample results. An unbiased random sample and a representative sample are important when drawing conclusions from the results of a study.

“WEIRD” Culture Samples

Psychologists have been guilty of largely recruiting samples of convenience from the thin slice of humanity—students—found at universities and colleges (Sears, 1986). This presents a problem when trying to assess the social mechanics of the public at large. Aside from being an overrepresentation of young, middle-class Caucasians, college students may also be more compliant and more susceptible to attitude change, have less stable personality traits and interpersonal relationships, and possess stronger cognitive skills than samples reflecting a wide range of age and experience (Peterson & Merunka, 2014; Visser, Krosnick, & Lavrakas, 2000). Put simply, these traditional samples (college students) may not be sufficiently representative of the broader population. Furthermore, considering that 96% of participants in psychology studies come from western, educated, industrialized, rich, and democratic countries (so-called WEIRD cultures; Henrich, Heine, & Norenzayan, 2010), and that the majority of these are also psychology students, the question of non-representativeness becomes even more serious. Of course, when studying a basic cognitive process (like working memory capacity) or an aspect of social behavior that appears to be fairly universal (e.g., even cockroaches exhibit social facilitation), a non-representative sample may not be a big deal. Over time research has repeatedly demonstrated the important role that individual differences (e.g., personality traits, cognitive abilities, etc.) and culture (e.g., individualism versus collectivism) play in shaping social behavior. For instance, even if we only consider a tiny sample of research on aggression, we know that narcissists are more likely to respond to criticism with aggression (Bushman &Baumeister, 1998); conservatives, who have a low tolerance for uncertainty, are more likely to prefer aggressive actions against those considered to be ‘outsiders’(de Zavala et al., 2010); countries, where men hold the bulk of the power in society, have higher rates of physical aggression directed against female partners (Archer, 2006); and males from the southern part of the United States are more likely to react with aggression following an insult (Cohen et al., 1996 ).

Why does random sampling work?

Below is an example showing how many credit hours students are currently enrolled in at a community college. This data represents the entire population of interest, all students currently enrolled in classes at Chandler-Gilbert Community College. Let’s say we randomly selected one student out of the population and asked them how many credit hours they are currently taking. How likely would it be for this one student to represent the entire population? This is the first line showing 1 student reported taking 12 hours while the average credit hours for a CGCC student was 8 (population average).

Sample size (n)  Sample average Population average  Difference between Sample & Population   
1 12 8 4
2 15 8 7
5 9.8 8 1.8
25 9.5 8 1.5
250 8.3 8 0.3
2500 7.9 8 0.1

The larger the sample size, the more closely it represents the population.

As we can see from this activity, the larger our sample is, the more accurately it will represent the population from which it was drawn. This brings up a very important rule in research design. The larger the sample size is, the more accurately the sample will represent the population from which it was drawn. Also, if you are comparing groups, consider that the more diverse, or variable, individuals in each group are, the larger the sample needs to be to detect real differences between groups.  We will further dive into the importance of sample sizes with inferential statistics, but for now, consider that the larger the sample, the more likely the researcher will represent the population.

Type of Research Designs

Research studies come in many forms, and, just like with the different types of data we have, different types of studies tell us different things. The choice of research design is determined by the research question and the logistics involved. Though a complete understanding of different research designs is the subject for at least one full class, if not more, a basic understanding of the principles is useful here. There are three types of research designs we will discuss: non-experimental, quasi-experimental, and random experimental.

Non-Experimental Designs

Non-experimental research (sometimes called correlational research) involves observing things as they occur naturally and recording our observations as data. In observational studies, information is gathered from observing.  This could include self-report as well as interviews.

Consider this example: A data scientist wants to know if there is a relation between how conscientious a person is and whether that person is a good employee. She hopes to use this information to predict the job performance of future employees by measuring their personality when they are still job applicants. She randomly samples volunteer employees from several different companies, measuring their conscientiousness and having their bosses rate their performance on the job. She analyzes this data to find a relation. Conscientiousness is a person-based variable that researcher must gather data from employees as they are in order to find a relation between her variables.

This type of research design cannot establish causality, it can still be quite useful. If the relation between conscientiousness and job performance is consistent, then it doesn’t necessarily matter is conscientiousness causes good performance or if they are both caused by something else – she can still measure conscientiousness to predict future performance. Additionally, these studies have the benefit of reflecting reality as it actually exists since we as researchers do not change anything.

Experimental Designs

If we want to know if a change in one variable causes a change in another variable, we must use a true experiment. A true experiment is an experimental design with random assignment.  In an experimental design a researcher assigns or manipulates, the group’s participants will be in. Further, each participant is randomly assigned to a group. If there is no random assignment, the experiment can not have cause-effect conclusions.

Types of Variables in an Experiment

When conducting research, experimenters often manipulate variables. For example, an experimenter might compare the effectiveness of four types of antidepressants. In this case, the variable is “type of antidepressant.” When a variable is manipulated by an experimenter, it is called an independent variable. The experiment seeks to determine the effect of the independent variable on relief from depression. In this example, relief from depression is called a dependent variable. In general, the independent variable is manipulated by the experimenter and its effects on the dependent variable are measured.

To understand what this means, let’s look at an example: A clinical researcher wants to know if a newly developed drug is effective in treating the flu. Working with collaborators at several local hospitals, she randomly samples 40 flu patients and randomly assigns each one to one of two conditions: Group A receives the new drug and Group B received a placebo. She measures the symptoms of all participants after 1 week to see if there is a difference in symptoms between the groups.

In the example, the independent variable is the drug treatment; we manipulate it into 2 levels: new drug or placebo. Without the researcher administering the drug (i.e. manipulating the independent variable), there would be no difference between the groups. Each person, after being randomly sampled to be in the research, was then randomly assigned to one of the 2 groups. That is, random sampling and random assignment are not the same thing and cannot be used interchangeably. For research to be a true experiment, random assignment must be used. For research to be representative of the population, random sampling must be used. The use of both techniques helps ensure that there are no systematic differences between the groups, thus eliminating the potential for sampling bias. The dependent variable in the example is flu symptoms. Barring any other intervention, we would assume that people in both groups, on average, get better at roughly the same rate. Because there are no systematic differences between the 2 groups, if the researcher does find a difference in symptoms, she can confidently attribute it to the effectiveness of the new drug.

Can you identify the independent and dependent variables?

Example #1: Can blueberries slow down aging? A study indicates that antioxidants found in blueberries may slow down the process of aging. In this study, 19-month- old rats (equivalent to 60-year-old humans) were fed either their standard diet or a diet supplemented by either blueberry, strawberry, or spinach powder (randomly assigned). After eight weeks, the rats were given memory and motor skills tests. Although all supplemented rats showed improvement, those supplemented with blueberry powder showed the most notable improvement.

  • What is the independent variable? (dietary supplement: none, blueberry, strawberry, and spinach)
  • What are the dependent variables? (memory test and motor skills test)

Example #2: Does beta-carotene protect against cancer? Beta-carotene supplements have been thought to protect against cancer. However, a study published in the Journal of the National Cancer Institute suggests this is false. The study was conducted with 39,000 women aged 45 and up. These women were randomly assigned to receive a beta-carotene supplement or a placebo, and their health was studied over their lifetime. Cancer rates for women taking the beta-carotene supplement did not differ systematically from the cancer rates of those women taking the placebo.

  • What is the independent variable? (supplements: beta-carotene or placebo)
  • What is the dependent variable? (occurrence of cancer)

Example #3: How bright is right? An automobile manufacturer wants to know how bright brake lights should be in order to minimize the time required for the driver of the following car to realize that the car in front is stopping and to hit the brakes.

  • What is the independent variable? (brightness of brake lights)
  • What is the dependent variable? (time to hit brakes)

Levels of an Independent Variable

In order to establish that one variable must cause a change in another variable and so a researcher will likely use two groups or levels in order to observe the changes and make comparisons.

  • Experimental (treatment) group is the group who are exposed to the independent variable (or the manipulation) by the researcher; the experimental group represents the treatment group.
  • Control group is the group who are not exposed to the treatment variable; the control group serves as the comparison group.

If an experiment compares an experimental treatment group with a control group, then the independent variable (type of treatment) has two levels: experimental and control. Further, if an experiment were comparing five types of diets, then the independent variable (type of diet) would have 5 levels. In general, the number of levels of an independent variable is the number of experimental conditions.  Another term for levels for the independent variable is groups, treatments, or conditions.

Scores from the experimental group are compared to scores in the control group and if there is a systematic difference between groups then there is evidence of a relationship between variables. Let’s use our earlier example of stress as a way to illustrate the experimental method. Let’s assume that a researcher examining stress wants to test the impact of a stress reduction program on the stress levels of students and recruits 100 students to participate. Students are randomly assigned to either the experimental group or the control group. The experimental group participates in the stress reduction program but the control group does not. The stress-reduction program is the independent variable and stress level is the dependent variable. At the end of the training program each group, the experimental group, and the control group complete a stress test, and the scores are compared. If the stress reduction program worked, then the stress levels for the experimental group should be lower than the stress levels for the control group.

Quasi-Experimental Designs

Quasi-experimental research involves getting as close as possible to the conditions of a true experiment when we cannot meet all requirements. Specifically, a quasi- experiment involves manipulating the independent variable but not randomly assigning people to groups. There are several reasons this might be used. First, it may be unethical to deny potential treatment to someone if there is good reason to believe it will be effective and that the person would unduly suffer if they did not receive it. Alternatively, it may be impossible to randomly assign people to groups.

Consider the following example: A professor wants to test out a new teaching method to see if it improves student learning. Because he is teaching two sections of the same course, he decides to teach one section the traditional way and the other section using the new method. At the end of the semester, he compares the grades on the final for each class to see if there is a difference.

In this example, the professor has manipulated his teaching method, which is the independent variable, hoping to find a difference in student performance, the dependent variable. However, because students enroll in courses, he cannot randomly assign the students to a particular group, thus precluding using a true experiment to answer his research question. Because of this, we cannot know for sure that there are no systematic differences between the classes other than teaching style and therefore cannot determine causality.

Extraneous and Confounding Variables

Sometimes in a research study things happen that make it difficult for a researcher to determine whether the independent variable caused the change in the dependent variable. These have special names.

  • An extraneous variable is something that occurs in the environment or happens to the participants that unintentionally (accidentally) influences the outcome of the study. An extraneous variable affects everyone in a study.In an experiment on the effect of expressive writing on health, for example, extraneous variables would include participant variables (individual differences) such as their writing ability, their diet, and their shoe size. They would also include situation or task variables such as the time of day when participants write, whether they write by hand or on a computer, and the weather. Extraneous variables pose a problem because many of them are likely to have some effect on the dependent variable. For example, participants’ health will be affected by many things other than whether or not they engage in expressive writing. This can make it difficult to separate the effect of the independent variable from the effects of the extraneous variables, which is why it is important to control extraneous variables by holding them constant.
  • A confounding variable is a type of extraneous variable that changes at the same time as the independent variable, making it difficult to discern which one is causing changes in the dependent variable.

Working with data

What are data?

The first important point about data is that data are – meaning that the word “data” is plural (though some people disagree with me on this). You might also wonder how to pronounce “data” – I say “day-tah”, but I know many people who say “dah-tah”, and I have been able to remain friends with them in spite of this. Now, if I heard them say “the data is” then that would be a bigger issue…

Operationalizing Variables

We need to have specifically defined how we are measuring our construct or our variable.  The act of defining how to measure your data is to operationalize.  Some variables are easier to define, like height or weight.  I can measure height in inches tall or weight in pounds.  Some other variables can be more open to measurement, like happiness or love.  How would I measure happiness?  Would I simply ask are you happy (yes or no)? Would I use a questionnaire for a self-report measure?  Would I rate individuals from observing them for happiness?  Would I ask their partner, teacher, parent, best friend about the person’s happiness? Researchers’ decisions on how to measure data is an important factor and helps to determine what kind of data is being used.

How would you measure happiness in a research study? Image Source

Qualitative and Quantitative Variables

Data are composed of variables, where a variable reflects a unique measurement or quantity. An important distinction between variables is between qualitative variables and quantitative variables. Qualitative variables are those that express a qualitative attribute such as hair color, eye color, religion, favorite movie, gender, and so on. Qualitative means that they describe a quality rather than a numeric quantity. Qualitative variables are sometimes referred to as categorical variables. For qualitative variables, response options are usually limited or fixed to a set of possible values. Assigning a person, animal or event to a category is done on the basis of some qualitative property. For example, in my stats course, I generally give an introductory survey, both to obtain data to use in class and to learn more about the students. One of the questions that I ask is “What is your favorite food?”, to which some of the answers have been: blueberries, chocolate, tamales, pasta, pizza, and mango. Those data are not intrinsically numerical; we could assign numbers to each one (1=blueberries, 2=chocolate, etc), but we would just be using the numbers as labels rather than as real numbers. 

Personality type, gender, and shirt sizes are all categorical, or qualitative, variables. The values of a qualitative variable do not necessarily imply order and do not produce numerical responses or use real numbers.  For example, there is an order to shirt size but shirt size is categorical and not number based. Another example is postal Zip Code data. Those numbers are represented as integers, but they don’t actually refer to a numeric scale; each zip code basically serves as a label or category representing a different region.  Because this data is not using real numbers, what we do with those numbers is constrained; for example, it wouldn’t make sense to compute the average of those numbers.

More commonly in statistics we will work with quantitative data, meaning data that are numerical. For example, here Table 1 shows the results from another question that I ask in my introductory class, which is “Why are you taking this class?”

Table 1: Counts of the prevalence of different responses to the question “Why are you taking this class?”
Why are you taking this class? Number of students
It fulfills a degree plan requirement 105
It fulfills a General Education Breadth Requirement 32
It is not required but I am interested in the topic 11
Other 4

Note that the students’ answers were qualitative, but we generated a quantitative summary of them by counting how many students gave each response. Quantitative variables are those variables that are measured in terms of numbers. Some examples of quantitative variables are height, weight, and shoe size.

Experimental studies can involve qualitative and quantitative data. In the study on the effect of diet discussed previously, the independent variable was type of supplement: none, strawberry, blueberry, and spinach. The variable “type of supplement” is a qualitative variable; there is nothing quantitative about it. In contrast, the dependent variable “memory test” is a quantitative variable since memory performance was measured on a quantitative scale (number correct).

Discrete and Continuous Variables

Variables such as number of children in a household are called discrete variables since the possible scores are discrete points on the scale. For example, a household could have three children or six children, but not 4.53 children. Other variables such as “time to respond to a question” are continuous variables since the scale is continuous and not made up of discrete steps. The response time could be 1.64 seconds, or it could be 1.64237123922121 seconds. Of course, the practicalities of measurement preclude most measured variables from being truly continuous.

Levels of Measurement

Numbers mean different things in different situations. Consider three answers below that appear to be the same, but they really are not. All three questions pertain to a running race that you just finished. The three 5s all look the same. However, the three variables (identification number, finish place, and time) are quite different. Because of these different variables, the way we interpret 5 is unique for each variable.

  • What number were you wearing in the race?
  • What place did you finish in?
  • How many minutes did it take you to finish the race?

To illustrate the difference, consider your friend who also ran the race. Their answers to the same three questions were 10, 10, and 10. If we take the first question by itself and know that you had a score of 5, and your friend had a score of 10, what can we conclude? We can conclude that your race identification number is different from your friend’s number. That is all we can conclude. On the second question, with scores of 5 and 10, what can we conclude regarding the place you and your friend finished in the race? We can state that you were faster than your friend in the race and, of course, that your finishing places are different. Comparing the 5 and 10 on the third question, what can we conclude? We could state that you ran the race twice as fast as your friend, you ran the race faster than your friend and that your time was different than your friend’s time. The point of this discussion is to demonstrate the relationship between the questions we ask, and what the answers to those questions can tell us . Chances are, much of your past experience with numbers has been with pure numbers or with measurements such as time, length, and amount. “Four is twice as much as two” is true for the pure numbers themselves and for time, length, and amount –but this statement would not be true for finish places in a race. Fourth place is not twice anything in relation to 2nd place. Fourth place is not twice as slow or twice as far behind the 2nd place runner. The types of descriptive and inferential statistics we can use depend on the type of variable measured. Remember, a variable is defined as a characteristic we can measure that can assume more than one value.

For statistical analysis, exactly how the measurement is carried out depends on the type of variable involved in the analysis. Different types are measured differently. To measure the time taken to respond to a stimulus, you might use a stopwatch. Stopwatches are of no use, of course, when it comes to measuring someone’s attitude towards a political candidate. A rating scale is more appropriate in this case (with labels like “very favorable,” “somewhat favorable,” etc.). For a dependent variable such as “favorite color,” you can simply note the color-word (like “red”) that the subject offers.

Although procedures for measurement differ in many ways, they can be classified using a few fundamental categories. The psychologist S. S. Stevens suggested that scores can be assigned to individuals so that they communicate more or less quantitative information about the variable of interest (Stevens, 1946). Stevens actually suggested four different levels of measurement(which he called “scales of measurement”) that correspond to four different levels of quantitative information that can be communicated by a set of scores. In a given category, all of the procedures share some properties that are important for you to know about. The categories are called “scale types,” or just “scales,” and are described in this section.

Nominal scales

When measuring using a nominal scale, one simply names or categorizes responses. Gender, handedness, favorite color, and religion are examples of variables measured on a nominal scale. The essential point about nominal scales is that they do not imply any ordering among the responses. For example, when classifying people according to their favorite color, there is no sense in which green is placed “ahead of” blue. Responses are merely categorized. Nominal scales embody the lowest level of measurement.

Ordinal scales

A researcher wishing to measure consumers’ satisfaction with their microwave ovens might ask them to specify their feelings as either “very dissatisfied,” “somewhat dissatisfied,” “somewhat satisfied,” or “very satisfied.” The items in this scale are ordered, ranging from least to most satisfied. This is what distinguishes ordinal from nominal scales. Unlike nominal scales, ordinal scales allow comparisons of the degree to which two subjects possess the dependent variable. For example, our satisfaction ordering makes it meaningful to assert that one person is more satisfied than another with their microwave ovens. Such an assertion reflects the first person’s use of a verbal label that comes later in the list than the label chosen by the second person.

On the other hand, ordinal scales fail to capture important information that will be present in the other scales we examine. In particular, the difference between two levels of an ordinal scale cannot be assumed to be the same as the difference between two other levels. In our satisfaction scale, for example, the difference between the responses “very dissatisfied” and “somewhat dissatisfied” is probably not equivalent to the difference between “somewhat dissatisfied” and “somewhat satisfied.” Nothing in our measurement procedure allows us to determine whether the two differences reflect the same difference in psychological satisfaction.

Statisticians express this point by saying that the differences between adjacent scale values do not necessarily represent equal intervals on the underlying scale giving rise to the measurements. (In our case, the underlying scale is the true feeling of satisfaction, which we are trying to measure.)

What if the researcher had measured satisfaction by asking consumers to indicate their level of satisfaction by choosing a number from one to four? Would the difference between the responses of one and two necessarily reflect the same difference in satisfaction as the difference between the responses two and three? The answer is No. Changing the response format to numbers does not change the meaning of the scale. We still are in no position to assert that the mental step from 1 to 2 (for example) is the same as the mental step from 3 to 4.

(Equal) Interval scales

Interval scales are numerical scales in which intervals have the same interpretation throughout. As an example, consider the Fahrenheit scale of temperature. The difference between 30 degrees and 40 degrees represents the same temperature difference as the difference between 80 degrees and 90 degrees. This is because each 10-degree interval has the same physical meaning (in terms of the kinetic energy of molecules).

Interval scales are not perfect, however. In particular, they do not have a true zero point even if one of the scaled values happens to carry the name “zero.” The Fahrenheit scale illustrates the issue. Zero degrees Fahrenheit does not represent the complete absence of temperature (the absence of any molecular kinetic energy). In reality, the label “zero” is applied to its temperature for quite accidental reasons connected to the history of temperature measurement. Since an interval scale has no true zero point, it does not make sense to compute ratios of temperatures. For example, there is no sense in which the ratio of 40 to 20 degrees Fahrenheit is the same as the ratio of 100 to 50 degrees; no interesting physical property is preserved across the two ratios. After all, if the “zero” label were applied at the temperature that Fahrenheit happens to label as 10 degrees, the two ratios would instead be 30 to 10 and 90 to 40, no longer the same! For this reason, it does not make sense to say that 80 degrees is “twice as hot” as 40 degrees. Such a claim would depend on an arbitrary decision about where to “start” the temperature scale, namely, what temperature to call zero (whereas the claim is intended to make a more fundamental assertion about the underlying physical reality).

Ratio scales (Absolute zero)

The ratio scale of measurement is the most informative scale. It is an interval scale with the additional property that its zero position indicates the absence of the quantity being measured. You can think of a ratio scale as the three earlier scales rolled up in one. Like a nominal scale, it provides a name or category for each object (the numbers serve as labels). Like an ordinal scale, the objects are ordered (in terms of the ordering of the numbers). Like an interval scale, the same difference at two places on the scale has the same meaning. And in addition, the same ratio at two places on the scale also carries the same meaning.

The Fahrenheit scale for temperature has an arbitrary zero point and is therefore not a ratio scale. However, zero on the Kelvin scale is absolute zero. This makes the Kelvin scale a ratio scale. For example, if one temperature is twice as high as another as measured on the Kelvin scale, then it has twice the kinetic energy of the other temperature.

Another example of a ratio scale is the amount of money you have in your pocket right now (25 cents, 55 cents, etc.). Money is measured on a ratio scale because, in addition to having the properties of an interval scale, it has a true zero point: if you have zero money, this implies the absence of money. Since money has a true zero point, it makes sense to say that someone with 50 cents has twice as much money as someone with 25 cents (or that Bill Gates has a million times more money than you do).

Here is a decision tree that you might find helpful for classifying data into N-O-I-R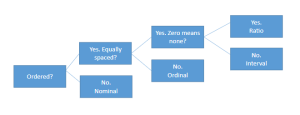N-O-I-R decision tree

Digging deeper: What about the number value? It is important to know what number values mean.  Is the number meaningful or it is a category? This section briefly reviews how numbers can be categorized according to meaning.

Binary numbers. The simplest are binary numbers – that is, zero or one. We will often use binary numbers to represent whether something is true or false, or present or absent. For example, I might ask 10 people if they have ever experienced a migraine headache, recording their answers as “Yes” or “No”. It’s often useful to instead use logical values, which take the value of either TRUE or FALSE. This can be especially useful for programming languages to analyze data, since these languages already understand the concepts of TRUE and FALSE. In fact, most programming languages treat truth values and binary numbers equivalently. The number 1 is equal to the logical value TRUE, and the number zero is equal to the logical value FALSE.

Integers. Integers are whole numbers with no fractional or decimal part. We most commonly encounter integers when we count things, but they also often occur in psychological measurement. For example, in my introductory survey I administer a set of questions about attitudes towards statistics (such as “Statistics seems very mysterious to me.”), on which the students respond with a number between 1 (“Disagree strongly”) and 7 (“Agree strongly”). Integers are discontinuous.

Real numbers. Most commonly in statistics we work with real numbers, which have a fractional/decimal part. For example, we might measure someone’s weight, which can be measured to an arbitrary level of precision, from kilograms down to micrograms. Real numbers can be discontinuous or continuous.

What level of measurement is used for psychological variables?

Rating scales are used frequently in psychological research. For example, experimental subjects may be asked to rate their level of pain, how much they like a consumer product, their attitudes about capital punishment, their confidence in an answer to a test question. Typically these ratings are made on a 5-point or a 7-point scale. These scales are ordinal scales since there is no assurance that a given difference represents the same thing across the range of the scale. For example, there is no way to be sure that a treatment that reduces pain from a rated pain level of 3 to a rated pain level of 2 represents the same level of relief as a treatment that reduces pain from a rated pain level of 7 to a rated pain level of 6.

In memory experiments, the dependent variable is often the number of items correctly recalled. What scale of measurement is this? You could reasonably argue that it is a ratio scale. First, there is a true zero point; some subjects may get no items correct at all. Moreover, a difference of one represents a difference of one item recalled across the entire scale. It is certainly valid to say that someone who recalled 12 items recalled twice as many items as someone who recalled only 6 items.

But number-of-items recalled is a more complicated case than it appears at first. Consider the following example in which subjects are asked to remember as many items as possible from a list of 10. Assume that (a) there are 5 easy items and 5 difficult items, (b) half of the subjects are able to recall all the easy items and different numbers of difficult items, while (c) the other half of the subjects are unable to recall any of the difficult items but they do remember different numbers of easy items. Some sample data are shown below.

Subject

Easy Items

Difficult Items

Score

A

0

0

1

1

0

0

0

0

0

0

2

B

1

0

1

1

0

0

0

0

0

0

3

C

1

1

1

1

1

1

1

0

0

0

7

D

1

1

1

1

1

0

1

1

0

1

8

Let’s compare (i) the difference between Subject A’s score of 2 and Subject B’s score of 3 and (ii) the difference between Subject C’s score of 7 and Subject D’s score of 8. The former difference is a difference of one easy item; the latter difference is a difference of one difficult item. Do these two differences necessarily signify the same difference in memory? We are inclined to respond “No” to this question since only a little more memory may be needed to retain the additional easy item whereas a lot more memory may be needed to retain the additional hard item. The general point is that it is often inappropriate to consider psychological measurement scales as either interval or ratio. You will often see in statistical software that the distinction is between nominal, ordinal, and interval/ratio.

Consequences of level of measurement

Why are we so interested in the type of scale that measures a dependent variable? The crux of the matter is the relationship between the variable’s level of measurement and the statistics that can be meaningfully computed with that variable. For example, consider a hypothetical study in which 5 children are asked to choose their favorite color from blue, red, yellow, green, and purple. The researcher codes the results as follows:

Color

Code

                    Blue

1

                    Red

2

Yellow

3

Green

4

Purple

5

This means that if a child said her favorite color was “Red,” then the choice was coded as “2,” if the child said her favorite color was “Purple,” then the response was coded as 5, and so forth. Consider the following hypothetical data:

Subject

Color

Code

1

Blue

1

2

Blue

1

3

Green

4

4

Green

4

5

Purple

5

Each code is a number, so nothing prevents us from computing the average code assigned to the children. The average happens to be 3, but you can see that it would be senseless to conclude that the average favorite color is yellow (the color with a code of 3). Such nonsense arises because favorite color is a nominal scale, and taking the average of its numerical labels is like counting the number of letters in the name of a snake to see how long the beast is.

Does it make sense to compute the mean of numbers measured on an ordinal scale? This is a difficult question, one that statisticians have debated for decades. The prevailing (but by no means unanimous) opinion of statisticians is that for almost all practical situations, the mean of an ordinally-measured variable is a meaningful statistic. However, there are extreme situations in which computing the mean of an ordinally-measured variable can be very misleading.

What makes a good measurement?

In many fields such as psychology, the thing that we are measuring is not a physical feature, but instead is an unobservable theoretical concept, which we usually refer to as a construct. For example, let’s say that I want to test how well you understand the distinction between the different types of numbers described above. I could give you a pop quiz that would ask you several questions about these concepts and count how many you got right. This test might or might not be a good measurement of the construct of your actual knowledge – for example, if I were to write the test in a confusing way or use language that you don’t understand, then the test might suggest you don’t understand the concepts when really you do. On the other hand, if I give a multiple-choice test with very obvious wrong answers, then you might be able to perform well on the test even if you don’t actually understand the material.

It is usually impossible to measure a construct without some amount of error. In the example above, you might know the answer, but you might misread the question and get it wrong. In other cases, there is error intrinsic to the thing being measured, such as when we measure how long it takes a person to respond on a simple reaction time test, which will vary from trial to trial for many reasons. We generally want our measurement error to be as low as possible, which we can acheive either by improving the quality of the measurement (for example, using a better time to measure reaction time), or by averaging over a larger number of individual measurements.

Sometimes there is a standard against which other measurements can be tested, which we might refer to as a “gold standard” – for example, measurement of sleep can be done using many different devices (such as devices that measure movement in bed), but they are generally considered inferior to the gold standard of polysomnography (which uses measurement of brain waves to quantify the amount of time a person spends in each stage of sleep). Often the gold standard is more difficult or expensive to perform, and the cheaper method is used even though it might have greater error.

When we think about what makes a good measurement, we usually distinguish two different aspects of a good measurement: it should be reliable, and it should be valid.

Reliability

Reliability refers to the consistency of our measurements. One common form of reliability, known as “test-retest reliability”, measures how well the measurements agree if the same measurement is performed twice. For example, I might give you a questionnaire about your attitude towards statistics today, repeat this same questionnaire tomorrow, and compare your answers on the two days; we would hope that they would be very similar to one another, unless something happened in between the two tests that should have changed your view of statistics (like reading this book!).

Another way to assess reliability comes in cases where the data include subjective judgments. For example, let’s say that a researcher wants to determine whether a treatment changes how well an autistic child interacts with other children, which is measured by having experts watch the child and rate their interactions with the other children. In this case we would like to make sure that the answers don’t depend on the individual rater — that is, we would like for there to be high inter-rater reliability. This can be assessed by having more than one rater perform the rating, and then comparing their ratings to make sure that they agree well with one another.

Reliability is important if we want to compare one measurement to another, because the relationship between two different variables can’t be any stronger than the relationship between either of the variables and itself (i.e., its reliability). This means that an unreliable measure can never have a strong statistical relationship with any other measure. For this reason, researchers developing a new measurement (such as a new survey) will often go to great lengths to establish and improve its reliability.

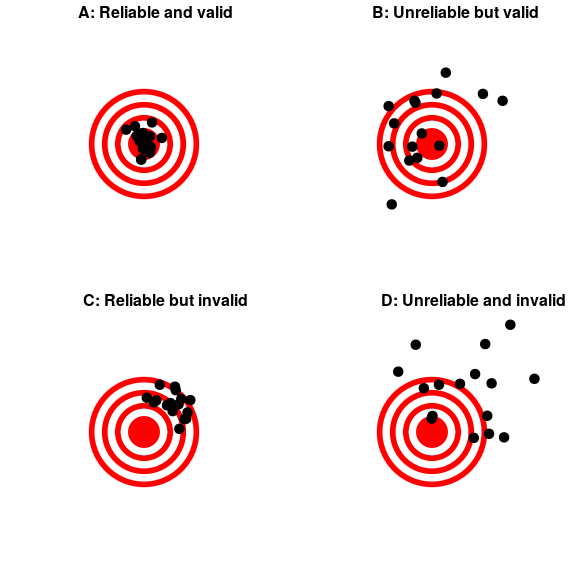
A figure demonstrating the distinction between reliability and validity, using shots at a bullseye. Reliability refers to the consistency of location of shots, and validity refers to the accuracy of the shots with respect to the center of the bullseye.

Figure 1: A figure demonstrating the distinction between reliability and validity, using shots at a bullseye. Reliability refers to the consistency of location of shots, and validity refers to the accuracy of the shots with respect to the center of the bullseye.

Validity

Reliability is important, but on its own it’s not enough: After all, I could create a perfectly reliable measurement on a personality test by re-coding every answer using the same number, regardless of how the person actually answers. We want our measurements to also be valid — that is, we want to make sure that we are actually measuring the construct that we think we are measuring (Figure 1). There are many different types of validity that are commonly discussed; we will focus on three of them.

Face validity. Does the measurement make sense on its face? If I were to tell you that I was going to measure a person’s blood pressure by looking at the color of their tongue, you would probably think that this was not a valid measure on its face. On the other hand, using a blood pressure cuff would have face validity. This is usually a first reality check before we dive into more complicated aspects of validity.

Construct validity. Is the measurement related to other measurements in an appropriate way? This is often subdivided into two aspects. Convergent validity means that the measurement should be closely related to other measures that are thought to reflect the same construct. Let’s say that I am interested in measuring how extroverted a person is using either a questionnaire or an interview. Convergent validity would be demonstrated if both of these different measurements are closely related to one another. On the other hand, measurements thought to reflect different constructs should be unrelated, known as divergent validity. If my theory of personality says that extraversion and conscientiousness are two distinct constructs, then I should also see that my measurements of extraversion are unrelated to measurements of conscientiousness.

Predictive validity. If our measurements are truly valid, then they should also be predictive of other outcomes. For example, let’s say that we think that the psychological trait of sensation seeking (the desire for new experiences) is related to risk taking in the real world. To test for predictive validity of a measurement of sensation seeking, we would test how well scores on the test predict scores on a different survey that measures real-world risk taking.

Critical Evaluation of Statistical Results

We need to evaluate the statistical studies we read about critically and analyze them before accepting the results of the studies. Common problems to be aware of include:

  • Problems with samples: A sample must be representative of the population. A sample that is not representative of the population is biased. Biased samples that are not representative of the population give results that are inaccurate and not valid.
  • Self-selected samples: Responses only by people who choose to respond, such as call-in surveys, are often unreliable.
  • Sample size issues: Samples that are too small may be unreliable. Larger samples are better, if possible. In some situations, having small samples is unavoidable and can still be used to draw conclusions. Examples: crash testing cars or medical testing for rare conditions.
  • Undue influence: collecting data or asking questions in a way that influences the response
  • Non-response or refusal of a participant to participate: The collected responses may no longer be representative of the population. Often, people with strong positive or negative opinions may answer surveys, which can affect the results.
  • Causality: A relationship between two variables does not mean that one causes the other to occur. They may be related (correlated) because of their relationship through a different variable.
  • Self-funded or self-interest studies: A study performed by a person or organization in order to support their claim. Is the study impartial? Read the study carefully to evaluate the
     work. Do not automatically assume that the study is good, but do not automatically assume the study is bad either. Evaluate it on its merits and the work done.
  • Misleading use of data: improperly displayed graphs, incomplete data, or lack of context
  • Confounding: When the effects of multiple factors on a response cannot be separated. Confounding makes it difficult or impossible to draw valid conclusions about the effect of each factor.

Types of Statistical Analyses

Now that we understand the nature of our data, let’s turn to the types of statistics we can use to interpret them. As mentioned at the end of chapter 1, there are 2 types of statistics: descriptive and inferential.

Descriptive Statistics

Descriptive statistics are numbers that are used to summarize and describe data. The word “data” refers to the information that has been collected from an experiment, a survey, an historical record, etc. (By the way, “data” is plural. One piece of information is called a “datum.”) If we are analyzing birth certificates, for example, a descriptive statistic might be the percentage of certificates issued in New York State, or the average age of the mother. Any other number we choose to compute also counts as a descriptive statistic for the data from which the statistic is computed. Several descriptive statistics are often used at one time to give a full picture of the data.

Descriptive statistics are just descriptive. They do not involve generalizing beyond the data at hand. Generalizing from our data to another set of cases is the business of inferential statistics, which you’ll be studying in another section. Here we focus on (mere) descriptive statistics.

Some descriptive statistics are shown in Table 2. The table shows the average salaries for various occupations in the United States in 1999.

Salary 1999

Salary 2019

Occupation

$112,760

$175,310

pediatricians

$106,130

$155,600

dentists

$100,090

$126,240

podiatrists

$76,140

$97,152

physicists

$53,410

$80,750

architects

$49,720

$78,200

school, clinical, and counseling psychologists

$47,910

$56,640

flight attendants

$39,560

$59,670

elementary school teachers

$38,710

$65,170

police officers

$18,980

$28, 040

floral designers

Table 2. Average salaries for various occupations in 1999 and 2019 (median salaries reported by Bureau of Labor Statistics).

Descriptive statistics like these offer insight into American society. It is interesting to note, for example, that we pay the people who educate our children and who protect our citizens a great deal less than we pay people who take care of our feet or our teeth.

For more descriptive statistics, consider Table 3. It shows the number of employed single young men to single young women for large metro areas in the US (reported in 2014). From this table we see that men outnumber women most in the San Jose, CA area, and women outnumber men most in the Memphis, TN area. You can see that descriptive statistics can be useful if we are looking for an opposite-sex partner between the ages of 25-34 years old! (These data come from Pew Research)

Highest Ratios of Employed Single Men to Single Women (25-34 y/o) Men per 100 Women Lowest Ratios of Employed Single Men to Single Women (25-34 y/o) Men per 100 Women
1. San-Jose-Sunnyvale-Santa Clara, CA

114

 1. Memphis, TN-MS-AR

59
2. Denver-Aurora-Lakewood, CO

101

 2. Jacksonville, FL

70
3. San Diego-Carlsbad, CA

99

 3. Detroit-Warren-Dearborn, MI

71
4. Minneapolis-St. Paul-Bloomington, MN-WI

98

 4. Charlotte-Concord-Gastonia, NC-SC

73
5. Seattle-Tacoma-Bellevue, WA

96

 5. Philadelphia-Camden-Wilmington, PA-NJ-DE-MD

74
6. San Francisco-Oakland-Hayward, CA

93

 6. Kansas City, MO-KS

75
7. Washington-Arlington-Alexandra, DC-VA-MD-WV            92 7. Nashville-Davidson-Murfreesboro-Franklin, TN

77
8. Los Angeles-Long Beach-Anaheim, CA

91

 8. Miami-Fort Lauderdale-West-Palm Beach, FL

78
9. Pittsburgh, PA

90

 9. New Orleans-Metairie, LA

78
10. Orlando-Kissimmee-Sanford, FL

90

 10. Cincinnati, OH-KY-IN

78

Table 3. Number of employed, 25-34 year old ratio of men to women in large metro areas of the U.S. (Pew Research, 2014)

These descriptive statistics may make us ponder why there are ratio differences in these large metropolitan areas. You probably know that descriptive statistics are central to the world of sports. Every sporting event produces numerous statistics such as the shooting percentage of players on a basketball team. For the Olympic marathon (a foot race of 26.2 miles), we possess data that cover more than a century of competition. (The first modern Olympics took place in 1896.) The following table shows the winning times for both men and women (the latter have only been allowed to compete since 1984).

Women

Year

Winner

Country

Time

1984

Joan Benoit

USA

2:24:52

1988

Rosa Mota

POR

2:25:40

1992

Valentina Yegorova

UT

2:32:41

1996

Fatuma Roba

ETH

2:26:05

2000

Naoko Takahashi

JPN

2:23:14

2004

Mizuki Noguchi

JPN

2:26:20

2008

Constantina Dita-Tomescu

Romania

2:26:44

2012

Tiki Gelana

ETH

2:23:07

2016

Jemima Sumgong

Kenya

2:24:04

2020

Peres Jepchirchir

Kenya

2:27:20

Men

Year

Winner

Country

Time

1896

Spiridon Louis

GRE

2:58:50

1900

Michel Theato

FRA

2:59:45

1904

Thomas Hicks

USA

3:28:53

1906

Billy Sherring

CAN

2:51:23

1908

Johnny Hayes

USA

2:55:18

1912

Kenneth McArthur

S. Afr.

2:36:54

1920

Hannes Kolehmainen

FIN

2:32:35

1924

Albin Stenroos

FIN

2:41:22

1928

Boughra El Ouafi

FRA

2:32:57

1932

Juan Carlos Zabala

ARG

2:31:36

1936

Sohn Kee-Chung

JPN

2:29:19

1948

Delfo Cabrera

ARG

2:34:51

1952

Emil Ztopek

CZE

2:23:03

1956

Alain Mimoun

FRA

2:25:00

1960

Abebe Bikila

ETH

2:15:16

1964

Abebe Bikila

ETH

2:12:11

1968

Mamo Wolde

ETH

2:20:26

1972

Frank Shorter

USA

2:12:19

1976

Waldemar Cierpinski

E.Ger

2:09:55

1980

Waldemar Cierpinski

E.Ger

2:11:03

1984

Carlos Lopes

POR

2:09:21

1988

Gelindo Bordin

ITA

2:10:32

1992

Hwang Young-Cho

S. Kor

2:13:23

1996

Josia Thugwane

S. Afr.

2:12:36

2000

Gezahenge Abera

ETH

2:10.10

2004

Stefano Baldini

ITA

2:10:55

2008

Samuel Wanjiru

Kenya

2:06:32

2012

Stephen Kiprotich

Uganda

2:08:01

2016

Eliud Kipchoge

Kenya

2:08:44

2020

Eliud Kipchoge

Kenya

2:08:38

Table 4. Winning Olympic marathon times.

There are many descriptive statistics that we can compute from the data in the table. To gain insight into the improvement in speed over the years, let us divide the men’s times into two pieces, namely, the first 13 races (up to 1952) and the second 13 (starting from 1956). The mean winning time for the first 13 races is 2 hours, 44 minutes, and 22 seconds (written 2:44:22). The mean winning time for the second 13 races is 2:13:18. This is quite a difference (over half an hour). Does this prove that the fastest men are running faster? Or is the difference just due to chance, no more than what often emerges from chance differences in performance from year to year? We can’t answer this question with descriptive statistics alone. All we can affirm is that the two means are “suggestive.”

Examining Table 4 leads to many other questions. We note that Takahashi (the lead female runner in 2000) would have beaten the male runner in 1956 and all male runners in the first 12 marathons. This fact leads us to ask whether the gender gap will close or remain constant. When we look at the times within each gender, we also wonder how far they will decrease (if at all) in the next century of the Olympics. Might we one day witness a sub-2 hour marathon? The study of statistics can help you make reasonable guesses about the answers to these questions.

It is also important to differentiate what we use to describe populations vs what we use to describe samples. A population is described by a parameter; the parameter is the true value of the descriptive in the population, but one that we can never know for sure. For example, the Bureau of Labor Statistics reports that the average hourly wage of chefs or head cooks is $25.66[1]. However, even if this number was computed using information from every single chef in the United States (making it a parameter), it would quickly become slightly off as one chef retires and a new chef enters the job market. Additionally, as noted above, there is virtually no way to collect data from every single person in a population. In order to understand a variable, we estimate the population parameter using a sample statistic. Here, the term “statistic” refers to the specific number we compute from the data (e.g. the average), not the field of statistics. A sample statistic is an estimate of the true population parameter, and if our sample is representative of the population, then the statistic is considered to be a good estimator of the parameter.

Even the best sample will be somewhat off from the full population, earlier referred to as sampling bias, and as a result, there will always be a tiny discrepancy between the parameter and the statistic we use to estimate it. This difference is known as sampling error, and, as we will see throughout the course, understanding sampling error is the key to understanding statistics. Every observation we make about a variable, be it a full research study or observing an individual’s behavior, is incapable of being completely representative of all possibilities for that variable.

Knowing where to draw the line between an unusual observation and a true difference is what statistics is all about.

Inferential Statistics

Descriptive statistics are wonderful at telling us what our data look like. However, what we often want to understand is how our data behave. What variables are related to other variables? Under what conditions will the value of a variable change? Are two groups different from each other, and if so, are people within each group different or similar? These are the questions answered by inferential statistics, and inferential statistics are how we generalize from our sample back up to our population. Units 2 and 3 are all about inferential statistics, the formal analyses and tests we run to make conclusions about our data.

For example, we will learn how to use a t statistic to determine whether people change over time when enrolled in an intervention. We will also use an F statistic to determine if we can predict future values on a variable based on current known values of a variable. There are many types of inferential statistics, each allowing us insight into a different behavior of the data we collect. This course will only touch on a small subset (or a sample) of them, but the principles we learn along the way will make it easier to learn new tests, as most inferential statistics follow the same structure and format.

Mathematical Notation

As noted above, statistics is not math. It does, however, use math as a tool. Many statistical formulas involve summing numbers. Fortunately there is a convenient notation for expressing summation. This section covers the basics of this summation notation.

Let’s say we have a variable X that represents the weights (in grams) of 4 grapes:

Grape

X

1

4.6

2

5.1

3

4.9

4

4.4

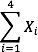
image

We label Grape 1’s weight X1, Grape 2’s weight X2, etc. The following formula means to sum up the weights of the four grapes:

The Greek letter Σ indicates summation. The “i = 1” at the bottom indicates that the summation is to start with X1 and the 4 at the top indicates that the summation will end with X4. The “Xi” indicates that X is the variable to be summed as i goes from 1 to 4. Therefore,

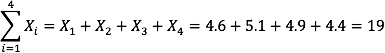
image

The symbol

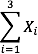
image

indicates that only the first 3 scores are to be summed. The index variable i goes from 1 to 3.

When all the scores of a variable (such as X) are to be summed, it is often convenient to use the following abbreviated notation:

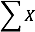
image

Thus, when no values of i are shown, it means to sum all the values of X.

Many formulas involve squaring numbers before they are summed. This is indicated as

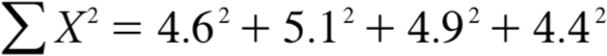
image

= 21.16 + 26.01 + 24.01 + 19.36 = 90.54

Notice that:

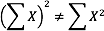
image

because the expression on the left means to sum up all the values of X and then square the sum (19² = 361), whereas the expression on the right means to square the numbers and then sum the squares (90.54, as shown).

Some formulas involve the sum of cross products. Below are the data for variables X and Y. The cross products (XY) are shown in the third column. The sum of the cross products is 3 + 4 + 21 = 28.

X

Y

XY

1

3

3

2

2

4

3

7

21

In summation notation, this is written as:

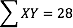
image

Three key concepts for statistical formulas:

  1. Perform summation in the correct order following the order of operations (PEMDAS).
  2. Typically we will use a set of scores for the mathematical operations/formulas used in statistics.
  3. Each operation, except for summation, creates a new column of numbers (we will see this in action in chapter 4).  Summation adds up the sum for the column and is typically seen as the last row.

Learning Objectives

Having read this chapter, you should be able to:

  • Familiarize with terminology and special notations of statistics.
  • Differentiate and identify different types of research design.
  • Differentiate and identify different types of sampling.
  • Distinguish between different types of variables and given examples of each of these kinds of variables.
  • Distinguish between the concepts of reliability and validity and apply each concept to a particular dataset.
  • Understand and list the three key concepts for using summation.

Exercises – Ch. 2

  1. In your own words, describe why we study statistics.
  2. For each of the following, determine if the variable is continuous or discrete:
    1. Time taken to read a book chapter
    2. Favorite food
    3. Cognitive ability
    4. Temperature
    5. Letter grade received in a class
  3. For each of the following, determine the level of measurement:
    1. T-shirt size
    2. Time taken to run 100 meter race
    3. First, second, and third place in 100 meter race
    4. Birthplace
    5. Temperature in Celsius
  4. What is the difference between a population and a sample? Which is described by a parameter and which is described by a statistic?
  5. What is sampling bias? What is sampling error?
  6. What is the difference between a simple random sample and a stratified random sample?
  7. What are the two key characteristics of a true experimental design?
  8. When would we use a quasi-experimental design?
  9. Use the following dataset for the computations below:
    X Y
    1 1
    2 3
    5 5
    7 1

    Computations to use for the above data set:

    1. ΣX
    2. ΣY2
    3. ΣXY
    4. (ΣY)2
  10. What are the most common measures of central tendency and spread?

Answers to Odd-Numbered Exercises – Ch. 2

  1. Your answer could take many forms but should include information about objectively interpreting information and/or communicating results and research conclusions
  2. For each of the following, determine the level of measurement:
    1. Ordinal
    2. Ratio
    3. Ordinal
    4. Nominal
    5. Interval
  3. Sampling bias is the difference in demographic characteristics between a sample and the population it should represent. Sampling error is the difference between a population parameter and sample statistic that is caused by random chance due to sampling bias.
  4. Random assignment to treatment conditions and manipulation of the independent variable
  5. Use the following dataset for the computations below:
    1. 15
    2. 36
    3. 39
    4. 100

 

  1. BLS, 5/2020, median value reported--to be explained in chapter 4 ↵

License

Icon for the Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License

Chapter 1: Statistical Thinking, Research Methods and Data Copyright © by Alisa Beyer is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, except where otherwise noted.

Share This Book