7.5: Solution Stoichiometry
Learning Objective
- Determine amounts of reactants or products in aqueous solutions using concentrations and stoichiometric problem solving techniques.
As we learned previously, double replacement reactions involve the reaction between ionic compounds in aqueous solution. In the course of the reaction, the ions in the two reacting compounds are “switched” (they replace each other). Because these reactions occur in aqueous solution, we can use the concept of molarity to directly calculate the number of moles of reactants or products that will be formed, and therefore their amounts (i.e. volume of solutions or mass of precipitates).
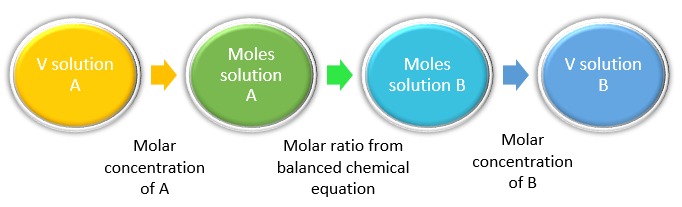
As an example, lead (II) nitrate and sodium chloride react to form sodium nitrate and the insoluble compound, lead (II) chloride.
Pb(NO3)2 (aq) + 2 NaCl (aq) → PbCl2 (s) + 2 NaNO3 (aq)
In the reaction shown above, if we mixed 0.123 L of a 1.00 M solution of NaCl with 1.50 M solution of Pb(NO3)2, we could calculate the volume of Pb(NO3)2 solution needed to completely precipitate the Pb2+ ions.
The molar concentration can also be expressed as the following:
[latex]1.00~M~NaCl[/latex] = [latex]\frac{1.00~mol~NaCl}{1~L~NaCl~solution}[/latex]
and
[latex]1.5~M~Pb(NO_3)_2[/latex] = [latex]\frac{1.50~mol~Pb(NO_3)_2}{1~L~Pb(NO_3)_2~solution}[/latex]
First, we must examine the reaction stoichiometry in the balanced reaction. In this reaction, one mole of Pb(NO3)2 reacts with two moles of NaCl to give one mole of PbCl2 precipitate. Thus, the concept map utilizing the stoichiometric ratios is:

so the volume of lead (II) nitrate that reacted is calculated as:
[latex]0.123~L~NaCl~solution[/latex] x [latex]\frac{1.00~mol~NaCl}{1~L~NaCl~solution}[/latex] x [latex]\frac{1~mol~Pb(NO_3)_2}{2~mol~NaCl}[/latex] x [latex]\frac{1~L~Pb(NO_3)_2~solution}{1.5~mol~Pb(NO_3)_2}[/latex] = [latex]0.041~Pb(NO_3)_2~L~solution[/latex]
This volume makes intuitive sense for two reasons: (1) the number of moles of Pb(NO3)2 required is half of the number of moles of NaCl, based off of the stoichiometry in the balanced reaction; (2) the concentration of Pb(NO3)2 solution is 50% greater than the NaCl solution, so less volume is needed.
Example 7.5.1
What volume (in L) of 0.500 M sodium sulfate will react with 275 mL of 0.250 M barium chloride to completely precipitate all Ba2+ in the solution?
Solution
| Steps for Problem Solving | |
| Identify the “given” information and what the problem is asking you to “find.” | Given: 275 mL BaCl2
0.250 M BaCl2 0.500 M Na2SO4 Find: Volume Na2SO4 solution |
| Set up and balance the chemical equation. | Na2SO4(aq) + BaCl2(aq) ⟶ BaSO4(s) + 2 NaCl(aq)
An insoluble product is formed after the reaction |
| List other known quantities. | 1 mol of Na2SO4 to 1 mol BaCl2
1000 mL = 1 L |
| Prepare a concept map and use the proper conversion factor. |  |
| Cancel units and calculate. | [latex]\scriptsize 275\cancel{mL \; BaCl_2 \; solution}\times \frac{1\cancel{L}}{1000\cancel{mL}}\times \frac{0.250 \cancel{mol \; BaCl_2}}{1 \cancel{L\;BaCl_2 \; solution}}\times \frac{1 \cancel{mol \; Na_2SO_4}}{1 \cancel{mol \; BaCl_2}}\times \frac{1\; L \; Na_2SO_4 \; solution}{0.500 \cancel{mol Na_2SO_4}}[/latex] = [latex]0.1375~L~sodium~sulfate[/latex] |
| Think about your result. | The lesser amount (almost half) of sodium sulfate is to be expected as it is more concentrated than barium chloride. Also, the units are correct. |
Exercise 7.5.1
What volume of 0.250 M lithium hydroxide will completely react with 0.500 L of 0.250 M of sulfuric acid solution?
Answer
0.250 L LiOH solution
Key Takeaways
- Performing stoichiometric calculations involving reactions that occur in solution is referred to as “solution stoichiometry”.
- Solution stoichiometry problems, like all stoichiometry problems, requires the use of a mole ratio from a balanced chemical equation.
- Use molarity, mol/L, as a conversion factor in solution stoichiometry problems.
Supplemental Video Support
Contributions & Attributions
- Paul R. Young, Professor of Chemistry, University of Illinois at Chicago, Wiki: AskTheNerd; PRY
 askthenerd.com – pyoung
askthenerd.com – pyoung uic.edu; ChemistryOnline.com
uic.edu; ChemistryOnline.com - Marisa Alviar-Agnew (Sacramento City College)
- Henry Agnew (UC Davis)

