"

2.2: Expressing Numbers

Learning Objectives

  • Learn to express numbers properly using both standard and scientific notation.
  • Learn to convert between standard and scientific notation.

Quantities have two parts: the number and the unit. The number tells “how many.” It is important to be able to express numbers properly so that the quantities can be communicated properly. The unit is the standard of measurement – are we measuring a quantity of some sort of matter in inches, kilometers, pounds, gallons, or some other unit?

Standard Notation

Scientific notation is an expression of a number using powers of 10. Powers of 10 are used to express very large or very small numbers in more concise ways. Table 2.2.1 shows the powers of 10. The left side has 10 to a specific power and the right side has the value for the specified power.

 

Table 2.2.1. Powers of Ten With Positive Exponents (Expressing Numbers That Are One Or Greater)
10 to Specific Power Value for Specified Power
100 = 1
101 = 10
102 = 10 x 10 = 100
103 = 10 x 10 x 10 = 1,000
104 = 10 x 10 x 10 x 10 = 10,000
… …

The raised number to the right of the 10 indicates the number of factors of 10 in the original number. (Scientific notation is sometimes called exponential notation.) The exponent’s value is equal to the number of zeros in the number expressed in standard notation.

Small numbers can also be expressed in scientific notation but with negative exponents. Table 2.2.2 shows the powers of 10 with negative exponents. The left side has 10 to a specific power and the right side has the value for the specified power.

Table 2.2.2: Powers of Ten With Negative Exponents (Expressing Numbers Less Than One)

10 to Specific Power Value for Specified Power
10-1 = 1/10 = .1
10-2 = 1/100 = .01
10-3 = 1/1,000 = .001
10-4 = 1/10,000 = .0001
… …

Again, the value of the exponent is equal to the number of zeros in the denominator of the associated fraction. A negative exponent implies a decimal number less than one.

A number is expressed in scientific notation by writing the first nonzero digit, then a decimal point, and then the rest of the digits. The part of a number in scientific notation that is multiplied by a power of 10 is called the coefficient. We determine the power of 10 needed to make that number into the original number and multiply the written number by the proper power of 10. For example, to write 79,345 in scientific notation,

79,345 = 7.9345 × 10,000 = 7.9345 × 104

Thus, the number in scientific notation is 7.9345 × 104. For small numbers, the same process is used, but the exponent for the power of 10 is negative:

0.000411 = 4.11 x [latex]\frac{1}{10,000}[/latex] = 4.11 x 10-4

Typically, the extra zero digits at the end or the beginning of a number are not included (Figure 2.2.1).

 

Image of the earth from space
Figure 2.2.1: “The Blue Marble” is a famous photograph of the Earth taken on December 7, 1972, by the crew of the Apollo 17 spacecraft en route to the Moon at a distance of about 29,000 kilometers. This is 2.9 × 104 km. It shows Africa, Antarctica, and the Arabian Peninsula. The earth is about 93,000,000 miles from the sun. In scientific notation, this is 9.3 × 107 miles. (Public Domain; NASA/Apollo 17 crew; taken by either Harrison Schmitt or Ron Evans.)

Example 2.2.1: Expressing Numbers in Scientific Notation

Express these numbers in scientific notation.

a. 306,000
b. 0.00884
c. 2,760,000
d. 0.000000559

Solution

a. The number 306,000 is 3.06 times 100,000, or 3.06 times 105. In scientific notation, the number is 3.06 × 105.

b. The number 0.00884 is 8.84 times 1/1,000, which is 8.84 times 10−3. In scientific notation, the number is 8.84 × 10−3.

c. The number 2,760,000 is 2.76 times 1,000,000, which is the same as 2.76 times 106. In scientific notation, the number is written as 2.76 × 106. Note that we omit the zeros at the end of the original number.

d. The number 0.000000559 is 5.59 times 1/10,000,000, which is 5.59 times 10−7. In scientific notation, the number is written as 5.59 × 10−7.

Exercise 2.2.1

 

Another way to determine the power of 10 in scientific notation is to count the number of places you need to move the decimal point to get a numerical value between 1 and 10. The number of places equals the power of 10. This number is positive if you move the decimal point to the right and negative if you move the decimal point to the left:

 

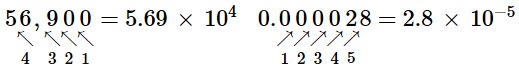
Figure 2.2.2: 56900 can be written as 5.69 times 10 to the fourth power. 0.000028 can be written as 2.8 times 10 to the negative fifth power.

Many quantities in chemistry are expressed in scientific notation. When performing calculations, you may have to enter a number in scientific notation into a calculator. Be sure you know how to correctly enter a number in scientific notation into your calculator. Different models of calculators require different actions for properly entering

Image of a calculator with the numbers 3.84951 times 10 to the eighteenth power.
Figure 2.2.3: This calculator shows only the coefficient and the power of 10 to represent the number in scientific notation. Thus, the number being displayed is 3.84951×1018, or 3,849,510,000,000,000,000. Source: “Casio” Asim Bijarani is licensed under Creative Commons Attribution 2.0 Generic.

Key Takeaways

  • The power of 10 is positive for numbers greater than 1 and negative for numbers between 0 and 1.

Supplemental Video Support

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License

CHM130 Fundamental Chemistry Copyright © by Mesa Community College is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License, except where otherwise noted.

Share This Book