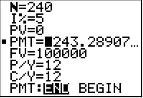Section PF.10 – Annuities
Most of us aren’t able to put a large sum of money in the bank today. Instead, we save by depositing a smaller amount of money from each paycheck into the bank. This idea is called a savings annuity. This is how most retirement accounts work.
In this course, we will assume that you put equal amounts of money into the account on a regular schedule (every month, year, quarter, etc.) and let it sit there earning interest.
Suppose you start out by making monthly deposits of $100.00 into an account that earns 12% annual interest. We assume that the account is compounded with the same frequency as we make deposits unless stated otherwise. If payments are made monthly, we assume interest is compounded monthly. If payments are made annually, we assume interest is compounded annually. We will also assume in this course that all compounding and payments occur at the END of the month.
In this example with monthly payments, we assume the 12% is compounded monthly (or 1% each month). So, you make your first $100.00 deposit at the end of the first month. At the end of the second month, you make another $100 deposit PLUS you earn 1% interest on the prior balance (in this case 1% of $100.00 = $1) making the balance in your account $201.00 at the end of month 2.
In general,
Ending Balance = Prior Balance + 1% Interest on Prior Balance + Monthly Payment
The table below shows this process repeated for 6 months.
| Month | Prior Balance | 1% Interest on Prior Balance | Monthly Payment | Ending Balance |
| 1 | $0.00 | $0.00 | $100.00 | $100.00 |
| 2 | $100.00 | $1.00 | $100.00 | $201.00 |
| 3 | $201.00 | $2.01 | $100.00 | $303.01 |
| 4 | $303.01 | $3.03 | $100.00 | $406.04 |
| 5 | $406.04 | $4.06 | $100.00 | $510.10 |
| 6 | $510.10 | $5.10 | $100.00 | $615.20 |
This process can be generalized by the Annuity Formula.
| Annuity Formula |
|
A = [latex]\large\frac{PMT((1~+~\frac{r}{n})^{nt}~-~1)}{(\frac{r}{n})}[/latex] A is the balance in the account after t years. PMT is the regular deposit (the amount you deposit each year, each month, etc.) r is the annual interest rate (APR) in decimal form (Example: 5% = 0.05) n is the number of compounding periods in one year t is the number of years we plan to make equal periodic deposits |
If the compounding frequency is not explicitly stated, assume there are the same number of compounds in a year as there are deposits made in a year. For example, if the compounding frequency isn’t stated then:
If you make your deposits every month, use monthly compounding, n = 12.
If you make your deposits every year, use yearly compounding, n = 1.
If you make your deposits every quarter, use quarterly compounding, n = 4.
Etc…
| When do you use the Annuity formula, Compound Interest formula, or Simple Interest formula? |
|
If you put money in the account on a regular schedule (every month, year, quarter, etc.) and let it sit there earning interest, then you need to use the Annuity formula. If you put money in the account once and let it sit there earning interest, then it is either the Simple Interest or Compound Interest formula depending on whether or not the interest is periodically added to the balance. Simple Interest: When you are given a starting principal/balance (only one deposit) and the interest is not being added to the balance (not compounding interest). (Section 2.4) Compound interest: When you are given a starting principal/balance (only one deposit) and the interest is periodically added to the balance (compounding interest). (Section 2.5) Annuity: When you start with zero balance, make repeated deposits on a regular schedule, and the interest is periodically added to the balance (compounding interest). (Section 2.7) |
| Example 1 |
|
In each scenario below, determine if you should use the Annuity formula, Compound Interest formula, or Simple Interest formula. • You borrow $200.00 from a friend to repair your car. Your friend charges you 2% interest. You repay the loan in a year and the interest will be calculated when you pay them back. How much interest will you pay your friend? • You charge $200.00 on your credit card. Your credit card charges 14% interest. The interest is calculated daily and added to your balance. What will your balance be in one year if you don’t make any payments? • You want to save up for a new motorcycle. You decide to open a saving account and deposit $200.00 in it every month. Your bank pays you interest on your account balance every month. The interest is added to your account every month. How much will you have saved in two years? |
| Example 2 | ||||
| A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If Charlotte deposits $100.00 each month into an IRA earning 6% interest, how much will she have in the account after 20 years? | ||||
|
In this example, PMT = $100 the monthly deposit r = 0.06 6% annual rate n = 12 since we’re doing monthly deposits, we’ll compound monthly t = 20 we want the amount after 20 years Putting this into the equation:
Charlotte’s account will grow to $46,204.09 after 20 years. Notice that she deposited into the account a total of $24,000 ($100 a month for 240 months). The difference between what she ends up with and how much she put in is the interest earned. In this case it is $46,204.09 - $24,000.00 = $22,204.09. |
In the example above, each step was shown individually to demonstrate how to work your way through this formula when doing the steps by hand. The TVM Solver program on your graphing calculator can perform this calculation for you, and do it much quicker! The guide on the next page will introduce you to using the TVM solver with annuities.
| Using the TVM Solver on your TI - Graphing Calculator |
|
Press APPS, then Finance, and TVM Solver (Note: If you have an older TI-83 calculator and do not have an APPS key, look for a key labeled Finance.) You will see a screen like the following: (Note: You will see different numbers after each parameter. There’s no reason to reset to zero--you will type right over them.)
N: Total number of payment/compounding periods (this is n*t where n is the number of compounding per year and t is the time in years) I%: Annual interest rate (APR) (Entered as a percent, NOT as a decimal.) PV: Present Value (the principal or beginning amount) PMT: Payment Amount (must be equal regular payments) FV: Future Value (accumulated value or end amount) P/Y: Number of payment periods per year C/Y: Number of compounding periods per year 'PMT:' For this class, keep the setting on END, indicating end-of-the month payments. For our applications, C/Y will always be the same value as P/Y. If you change P/Y, your calculator will automatically reset C/Y. NOTES:
TVM Solver will calculate the value of ANY of the first five values in the above list (N, I%, PV, PMT or FV) if the other four values are known. To solve for an unknown value, you will put the curser on the line you wish to find and then press SOLVE (press ALPHA, then the ENTER key). |
| Example 3 – Repeat of Example 2 using the TVM Solver |
| A traditional individual retirement account (IRA) is a special type of retirement account in which the money you invest is exempt from income taxes until you withdraw it. If you deposit $100.00 each month into an IRA earning 6% interest. How much will you have in the account after 20 years? |
|
We are looking for the future value (FV) of this account after 20 years. In this example, N = 20*12 Once all of the given parameters are entered in, move your cursor to FV= and press ALPHA – ENTER. FV = 46,204.08952 so the future value (ending balance) will be $46,204.09. |
| Example 4 | |||||||
| You want to have $200,000.00 in your account when you retire in 30 years. Your retirement account earns 8% interest. How much do you need to deposit each month to meet your retirement goal? | |||||||
|
In this example, we’re looking for PMT. r = 0.08 8% annual rate By hand, we could set up the equation, and solve for PMT:
Using the TVM Solver: We are looking for the monthly deposit required (PMT) to have a future value of $200,000.00 in the account after 30 years, with an annual interest rate of 8%. In this example, N = 30*12 Once all of the given parameters are entered in, move your cursor to PMT = and press ALPHA – ENTER. PMT = -134.20. So you would need to deposit $134.20 each month to have $200,000.00 in 30 years if your account earns 8% interest. |
| You Try PF.10.A |
| A more conservative investment account pays 3% interest. If you deposit $5.00 a day into this account, how much will you have after 10 years? How much is from interest? |
| Example 5 |
| You want to have $200,000.00 in your account when you retire in 30 years. Your retirement account earns 8.2% interest. How much do you need to deposit each month to meet your retirement goal? |
|
In this example, N = 30*12 Once all of the given parameters are entered in, move your cursor to PMT= and press ALPHA – ENTER. PMT = -128.84224 so you will need to deposit $128.85 each month to reach the goal. |
| You Try PF.10.B |
| If you want to end up with $30,000.00 after 5 years in an account earning 5.2% interest, compounded monthly, how much is your monthly deposit? |
| Example 6 |
| Emily invests $250.00 a month for 5 years into an account earning 4% interest compounded monthly. After 5 years, she leaves the money, without making additional deposits, in the account for another 25 years. How much will Emily have in the end? |
|
This problem requires two steps. Step 1: Initially, monthly deposits are being made into a saving annuity for a period of 5 years. This is new for section 6.1. Step 2: After that, the amount that has accrued from step 1 will sit (as a lump sum) and continue to earn compound interest for 25 more years. This is regular compound interest from section 5.2. Step 1: Find the amount in the account after monthly payments are made for 5 years. N = 12*5 Once all of the given parameters are entered in, move your cursor to FV= and press ALPHA – ENTER. FV = $16,574.74. After 5 years of making monthly payments, Emily will have $16,574.74 in the account. Step 2: Find the amount in the account after 25 years. Recall, the compound interest formula is: A = [latex]P_0(1~+~\frac{r}{n})^{nt}[/latex] A = 16,574.74(1 + [latex]\frac{0.04}{12}[/latex])12*25 A = 16,574.741 + 0.041212 * 25 A = 44,979.95 The final amount Emily will have in the account is $44,979.95 |
Section PF.10– Answers to You Try Problems
PF.7.A
After 10 years, you will have $21,282.07 in the account. $3,032.07 is from interest.
PF.7.B
Your monthly deposit should be $438.89.