Section G.3 – Triangles: The Pythagorean Theorem & Similarity
A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles (triangles with a 90° angle). He discovered that the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.
|
|
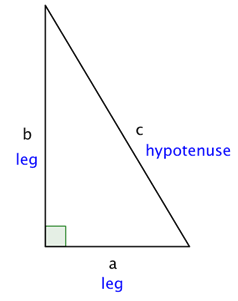
The Pythagorean Theorem If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. This relationship is represented by the formula: a 2 + b 2 = c 2
|
In the box above, you may have noticed the word “square,” as well as the small 2s to the top right of the letters in a2 + b2 = c2. To square a number means to multiply it by itself. So, for example, to square the number 5 you multiply 5 • 5, and to square the number 12, you multiply 12 • 12.
When you see the equation a2 + b2 = c2 , you can think of this as “the length of side a times itself, plus the length of side b times itself is the same as the length of side c times itself.”
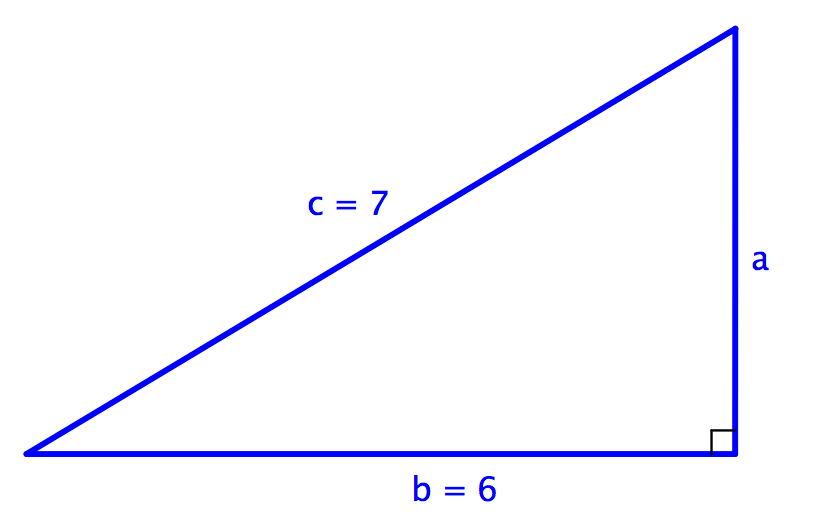
Let’s try out the Pythagorean Theorem with an actual right triangle.
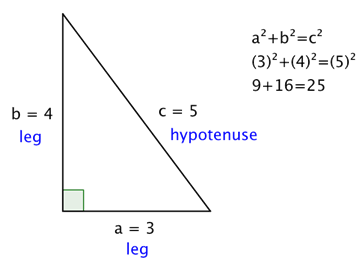
This theorem holds true for this right triangle—the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.
Note that the Pythagorean Theorem only works with right triangles.
|
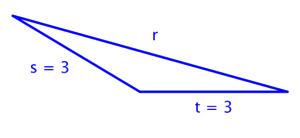
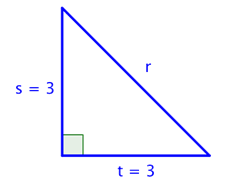
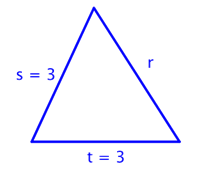
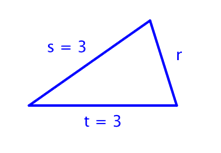
You Try G.3.A For which of these triangles is (3)2 + (3)2 = r2 ? Select all that apply.
|
Finding the Length of the Hypotenuse
You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle’s other two sides, called the legs. Put another way, if you know the lengths of a and b, you can find c.
| Example 1 | ||||||||||||
|
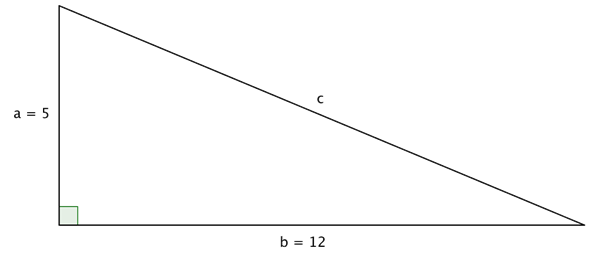
In the triangle above, you are given measures for legs a and b: 5 and 12, both in inches. Use the Pythagorean Theorem to find a value for the length of c, the hypotenuse. Then use your answer to find the perimeter of the triangle. |
||||||||||||
Using the formula, you find that the length of c, the hypotenuse, is 13 inches. You can then find the perimeter of the triangle by adding the length of all three sides. Perimeter = 5 inches + 12 inches + 13 inches = 30 inches |
Finding the Length of a Leg
You can use the same formula to find the length of a right triangle’s leg if you are given measurements for the lengths of the hypotenuse and the other leg. Consider the example below.
| Example 2 | |
|
Find the length of side a in the triangle below, the perimeter of the triangle, and the area of the triangle. Assume all units are in centimeters. Write your answer in exact form and in approximate form, rounded to the nearest thousandth.
|
|
|
a = ? |
In this right triangle, you are given the measurements for the hypotenuse, c, and one leg, b. The hypotenuse is always opposite the right angle and it is always the longest side of the triangle. |
|
a2 + b2 = c2 |
To find the length of leg a, substitute the known values into the Pythagorean Theorem. |
|
a2 + 36 = 49a2 = 13a = [latex]\small\sqrt{13}[/latex] |
Solve for a2. Answer: Exact form: a = 13; Approximate form: a ≈ 3.606 |
|
|
|
|
To find the perimeter, add up the lengths of all sides of the triangle. P = a + b + c Now that we know the height, we can use it to find the area of the triangle. A = [latex]\frac{1}{2}bh[/latex]
|
|
|
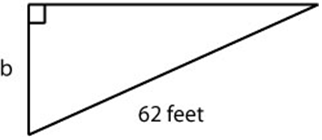
You Try G.3.B Find the length of side x in the triangle below, and the perimeter of the triangle. Assume all units are in centimeters. Write your answer in exact form and in approximate form, rounded to the nearest thousandth. 55 feet
|
Using the Theorem to Solve Real World Problems
The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real world settings. Architects and engineers use this formula when building ramps, bridges, and buildings. Consider the following:
| Example 3 | |
|
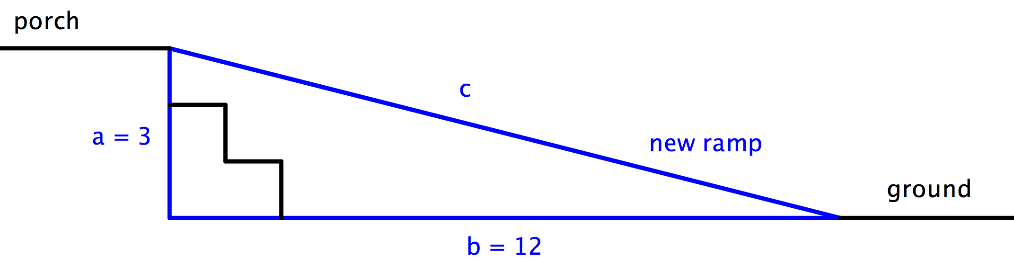
The owners of a house want to convert a stairway leading from the ground to their back porch into a ramp. The porch is 3 feet off the ground, and due to building regulations the ramp must start 12 feet away from the base of the porch. How long will the ramp be? Round your answer to the nearest tenth. |
|
|
To solve a problem like this one, it often makes sense to draw a simple diagram showing where the legs and hypotenuse of the triangle lie. |
|
|
|
|
|
a = 3 |
Identify the legs and the hypotenuse of the triangle. You know that the triangle is a right triangle since the ground and the raised portion of the porch are perpendicular—this means you can use the Pythagorean Theorem to solve this problem. Identify a, b, and c. |
|
a2 + b2 = c2
(3)2+(12)2 = c2
153 = c2
[latex]\sqrt{153}[/latex] = c
12.4 ≈ c
|
Use the Pythagorean Theorem to find the length of c. Use a calculator to find c. The square root of 153 is 12.369…, so you can round that to 12.4. |
|
The ramp will be 12.4 feet long. |
|
| Example 4 | |
|
A sailboat has a large sail in the shape of a right triangle. The longest edge of the sail measures 17 yards, and the bottom edge of the sail is 8 yards. How tall is the sail? |
|
|
|
Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side, so here it must be 17 yards. Set up the Pythagorean Theorem: a2 + b2 = c2 a2 + (8)2 =172 a2 + 64 = 289 a2 = 225 a = [latex]\sqrt{225}[/latex] a = 15 The height of the sail is 15 yards. |
|
You Try G.3.C You’ve decided to complete a “do it yourself” project and retile your bathroom floor. The tiles that you picked out are 12 inches by 12 inches. To make the pattern more interesting, you decide to cut the tiles in half along the diagonal, then place the cut edge of the tile along the wall (see the picture below). About how many ½ tiles will you need to make the first row, if the wall is 170 inches long?
|
Similarity
Triangles are similar if they have the same shape, but not necessarily the same size. You can think of it as “zooming in” or out making the triangle bigger or smaller, but keeping its basic shape.
Corresponding sides of similar triangles are proportional.
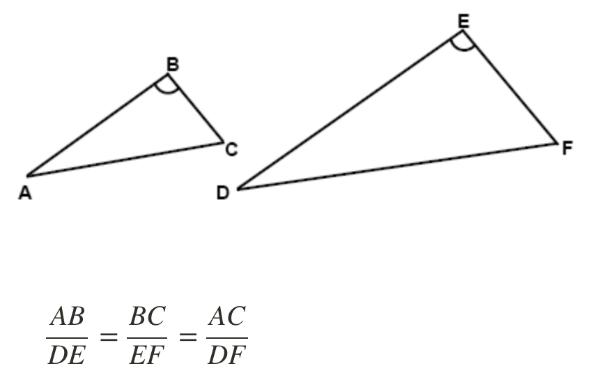
| Example 5 | |
|
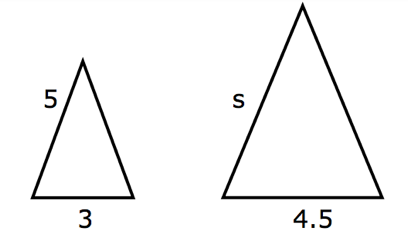
Find the length of the missing sides. |
|
|
a)
b)
|
Write a proportion relating the corresponding sides. [latex]\frac{5}{s}[/latex] = [latex]\frac{3}{4.5}[/latex] Solve the proportion using cross-products. 3 • s = 5 • 4.5 3s = 22.5 Divide each side by 3 to get s = 7.5. Write a proportion relating the corresponding sides. It might help to see the corresponding if you rotate one of the triangles so that the corresponding sides are aligned. [latex]\frac{2.1}{s}[/latex] = [latex]\frac{3.4}{10.2}[/latex] Solve the proportion using cross-products. 3.4 • s = 2.1 • 10.2 3.4s = 21.42 Divide each side by 3.4 to get s = 6.3.
|
| Example 6 |
|
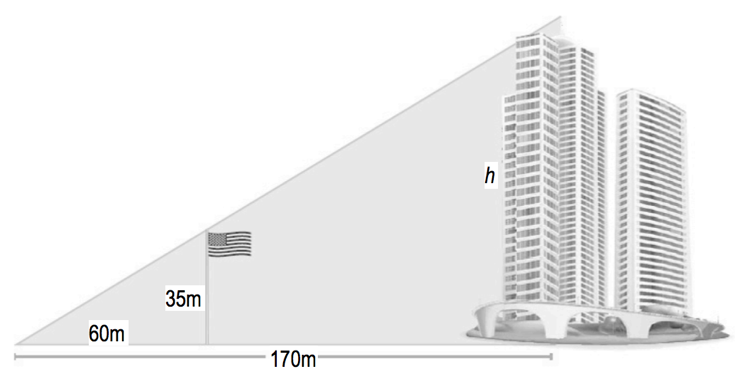
In the diagram below, a large flagpole stands outside of an office building. Marquis realizes that when he looks up from the ground, 60m away from the flagpole, that the top of the flagpole and the top of the building line up. If the flagpole is 35m tall, and Marquis is 170m from the building, how tall is the building?
[latex]\large\frac{h}{35}[/latex] = [latex]\frac{170}{60}[/latex] Solve the proportion using cross-products: 60h = 35 • 170 60h = 5,950 Divide each side by 60 to get h = 99.2. The height of the building is 99.2 m. |
Section G.3 – Answers to You Try Problems
G.3.A
B, because it is a right triangle.
G.3.B
Exact: [latex]\sqrt{819}[/latex] cm Approximate: 28.618 cm
G.3.C
You will need about 10 of the [latex]\frac{1}{2}[/latex] tiles.



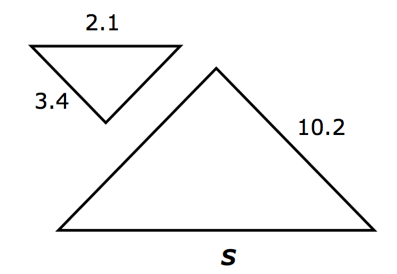
 Write a proportion relating the corresponding sides:
Write a proportion relating the corresponding sides: