Section G.6 - Working in Three Dimensions: Volume and Surface Area
Living in a two-dimensional world would be pretty boring. Thankfully, all of the physical objects that you see and use every day—computers, phones, cars, shoes—exist in three dimensions. They all have length, width, and height. (Even very thin objects like a piece of paper are three-dimensional. The thickness of a piece of paper may be a fraction of a millimeter, but it exists.)
In the world of geometry, it is common to see three-dimensional figures. In mathematics, a flat side of a three-dimensional figure is called a face. Polyhedrons are shapes that have four or more faces, each one being a polygon. These include cubes, prisms, and pyramids. Sometimes you may even see single figures that are composites of two of these figures. Let’s take a look at some common polyhedrons.
Identifying Solids
The first set of solids contains rectangular bases. Have a look at the table below, which shows each figure in both solid and transparent form.
|
Name |
Definition |
Solid Form |
Transparent Form |
|
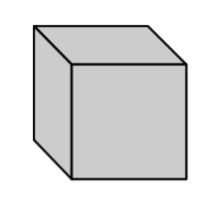
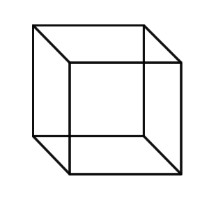
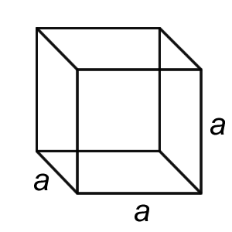
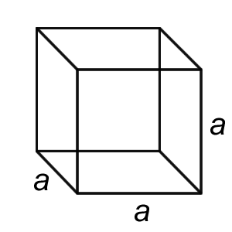
Cube |
A six-sided polyhedron that has congruent squares as faces. |
|
|
|
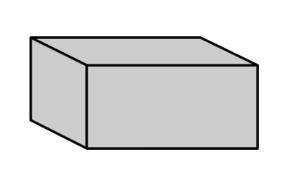
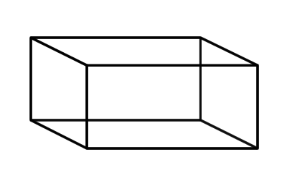
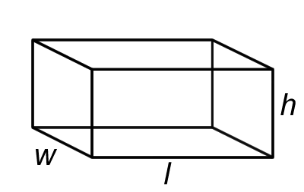
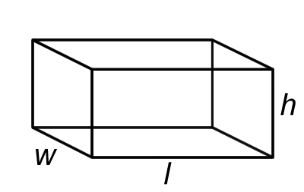
Rectangular prism |
A polyhedron that has three pairs of congruent, rectangular, parallel faces. |
|
|
|
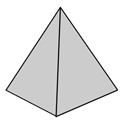
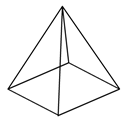
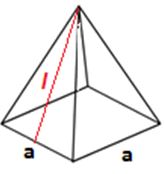
Pyramid |
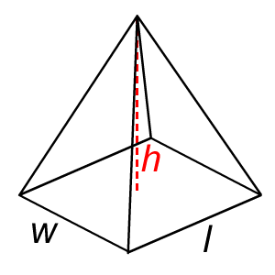
A polyhedron with a polygonal base and a collection of triangular faces that meet at a point. |
|
|
Notice the different names that are used for these figures. A cube is different than a square, although they are sometimes confused with each other—a cube has three dimensions, while a square only has two. Likewise, you would describe a shoebox as a rectangular prism (not simply a rectangle), and the ancient pyramids of Egypt as…well, as pyramids (not triangles)!
In this next set of solids, each figure has a circular base.
|
Name |
Definition |
Solid Form |
Transparent Form |
|
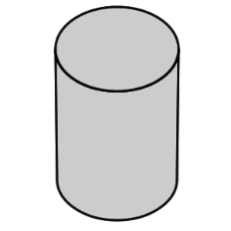
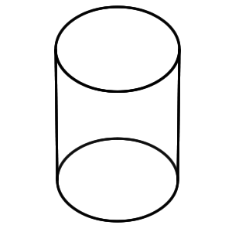
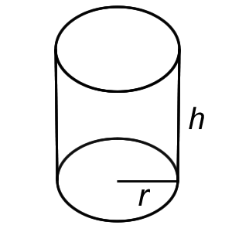
Cylinder |
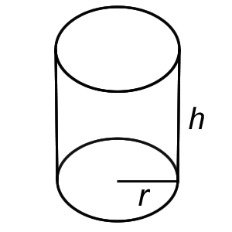
A solid figure with a pair of circular, parallel bases and a round, smooth face between them. |
|
|
|
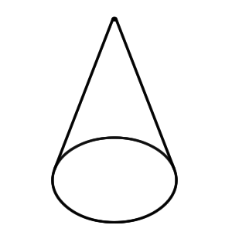
Cone |
A solid figure with a single circular base and a round, smooth face that diminishes to a single point. |
|
|
Take a moment to compare a pyramid and a cone. Notice that a pyramid has a rectangular base and flat, triangular faces; a cone has a circular base and a smooth, rounded body.
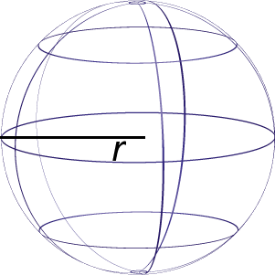
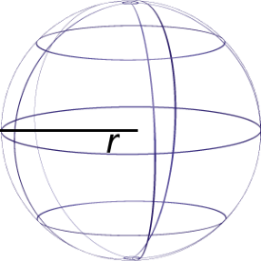
Finally, let’s look at a shape that is unique: a sphere. There are many spherical objects all around you—soccer balls, tennis balls, and baseballs being three common items.
|
Name |
Definition |
Solid Form |
Transparent Form |
|
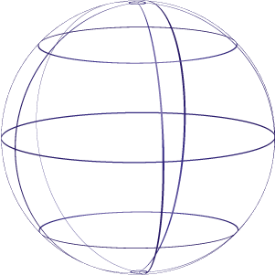
Sphere |
A solid, round figure where every point on the surface is the same distance from the center. |
|
|
Volume
Recall that perimeter measures one dimension (length), and area measures two dimensions (length and width). To measure the amount of space a three-dimensional figure takes up, you use another measurement called volume.
To visualize what “volume” measures, look back at the transparent image of the rectangular prism mentioned earlier (or just think of an empty shoebox). Imagine stacking identical cubes inside that box so that there are no gaps between any of the cubes. Imagine filling up the entire box in this manner. If you counted the number of cubes that fit inside that rectangular prism, you would have its volume.
Volume is measured in cubic units. The shoebox illustrated above may be measured in cubic inches (usually represented as in3 or inches3), while the Great Pyramid of Egypt would be more appropriately measured in cubic meters (m3 or meters3).
To find the volume of a geometric solid, you could create a transparent version of the solid, create a bunch of 1x1x1 cubes, and then stack them carefully inside. However, that would take a long time! A much easier way to find the volume is to become familiar with some geometric formulas, and to use those instead.
As you look through the list below, you may notice that some of the volume formulas look similar to their area formulas. To find the volume of a rectangular prism, you find the area of the base and then multiply that by the height.
| Name | Transparent Form | Volume Formula |
|
Cube |
|
V = a • a • a = a3 a = the length of one side |
|
Rectangular prism |
|
V = l • w • h l = length w = width h = height |
|
Pyramid |
|
V = [latex]\frac{{\pi}r^2h}{3}[/latex]
l = length w = width h = height |
Remember that all cubes are rectangular prisms, so the formula for finding the volume of a cube is the area of the base of the cube times the height.
Now let’s look at solids that have a circular base.
| Name | Transparent Form | Volume Formula |
|
Cylinder |
|
V = πr2h
r = radius h = height |
|
Cone |
|
V = [latex]\frac{{\pi}r^2h}{3}[/latex]
r = radius h = height |
Looking for patterns and similarities in the formulas can help you remember which formula refers to a given solid.
The volume of a cylinder is the area of its base, πr2 , times its height, h.
Compare the formula for the volume of a cone, V = [latex]\frac{{\pi}r^2h}{3}[/latex] , with the formula for the volume of a pyramid, V = [latex]\frac{l{\cdot}w{\cdot}h}{3}[/latex]
The numerator of the cone formula is the volume formula for a cylinder, and the numerator of the pyramid formula is the volume formula for a rectangular prism. Then divide each by 3 to find the volume of the cone and the pyramid.
Finally, the formula for a sphere is provided below. Notice that the radius is cubed, not squared and that the quantity πr3 is multiplied by [latex]\frac{4}{3}[/latex].
| Name |
Wireframe Form |
Volume Formula |
|
Sphere |
|
V= [latex]\frac{4}{3}[/latex]πr3
r = radius |
Applying the Formulas
You know how to identify the solids, and you also know the volume formulas for these solids. To calculate the actual volume of a given shape, all you need to do is substitute the solid’s dimensions into the formula and calculate. In the examples below, notice that cubic units (meters3, inches3, feet3) are used.
| Example 1 |
|
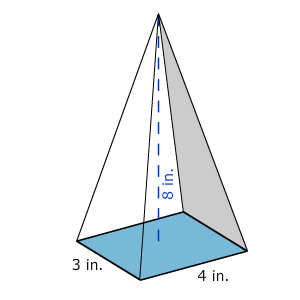
Find the volume of the shape shown below.
|
|
Identify the shape. It has a rectangular base and rises to a point, so it is a pyramid. |
|
Identify the proper formula to use. V = [latex]\frac{l{\cdot}w{\cdot}h}{3}[/latex] l = length, w = width, h = height |
|
Use the image to identify the dimensions. length = 4, width = 3, height = 8 Then substitute l = 4, w = 3, and h = 8 into the formula and calculate the volume. V = [latex]\frac{4{\cdot}3{\cdot}8}{3}[/latex] = [latex]\frac{96}{3}[/latex] =32 |
|
The volume of the pyramid is 32 inches3. |
| Example 2 | |
|
Find the volume of the shape shown below. Write your answer in exact form and approximate form, rounded to the nearest hundredth.
|
|
|
Identify the shape. It has a circular base and has uniform thickness (or height), so it is a cylinder. Identify the proper formula to use. V=πr2h |
|
|
Use the image to identify the dimensions. Then substitute r = 7 and h = 1 into the formula and calculate the volume. |
V = π(7)2(1)
V = π ∙ 49 ∙ 1
V = 49π
V ≈ 153.86
|
|
The volume is 49π or approximately 153.86 feet3. |
|
|
You Try G.6.A Determine the volume of a sphere with radius 6 feet. Write your answer in exact form and in approximate form, rounded to the nearest hundredth. Be sure to include correct units in your answer. |
Surface Area
In addition to volume, we can also measure the area of the outer surface of a three-dimensional object. This is known as the Surface Area. Like area, surface area is measured in square units.
| Name | Transparent Form | Surface Area Formula |
|
Cube |
|
SA = 6a2 a = the length of one side |
|
Rectangular prism |
|
SA = 2lw+2lh+2wh l = length |
|
Pyramid (Square Based) |
|
SA = a2 + 2al
a= length of one side |
|
Cylinder |
|
SA = 2πr2 + 2πrh
r = radius |
|
Cone |
|
SA = πr2 + πr[latex]\sqrt{r^2~+~h^2}[/latex]
r = radius |
|
Sphere |
|
SA = 4πr2
r = radius |
| Example 3 | |
|
Find the surface area of the shape shown below. Write your answer in exact form and approximate form (use the value of 3.14 for π), rounded to the nearest hundredth.
|
|
|
Identify the shape. It has a circular base and has uniform thickness (or height), so it is a cylinder. Identify the proper formula to use. SA = 2πr2 + 2πrh |
|
|
Use the image to identify the dimensions. Then substitute r = 7 and h = 1 into the formula and calculate the surface area. |
SA = 2π(7)2 + 2π(7)(1)
SA = 98π + 14π
SA = 112π
SA ≈ 1123.14 = 351.68
|
|
The surface area is 112π or approximately 351.68 feet2. |
|
| Example 4 | |
|
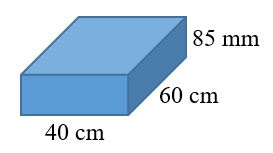
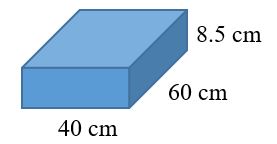
What is the minimum number of square centimeters of wrapping paper needed to wrap a rectangular box that is 40 cm wide, 60 cm long, and 85 mm high? |
|
|
Identify the shape. It is a rectangular box, which is a rectangular prism. Identify the proper formula to use. SA = 2lw + 2lh + 2wh Draw a sketch of the shape and label each side length.
Convert the height to centimeters.
|
|
|
Use the image to identify the dimensions. Then substitute w = 40 cm, l = 60 cm, and h = 8.5cm into the formula and calculate the surface area.
|
SA = 2lw + 2lh + 2wh
SA = 2(60)(40) + 2(60)(8.5) + 2(40)(8.5)
SA = 4800 + 1020 + 680
SA = 6500cm2
|
|
The surface area is 6500 cm2. |
|
| You Try G.6.B |
| What is the surface area of a giant papier-mâché model of the moon, which is a sphere with a diameter of 24 feet? Use 3.14 for the value of π. How many gallons of paint should be bought to paint the model? The paint is sold per gallon and each gallon will cover 350 square feet. |
Section G.6 - Answers to You Try Problems
G.6.A
Exact: 288π ft3
Approximate: 904.78 ft3
G.6.B
1808.64 ft2; 6 gallons need to be purchased