Section PC.0 – Sets and Venn Diagrams (Optional)
Section PC.0 – Sets and Venn Diagrams (Optional)
This section is intended for classes that are not covering Module SV - Sets and Venn Diagrams. It covers the basics of sets and Venn diagrams that are needed in Module PC.
Section PC.0 Learning Objectives:
- Use correct set notation and terminology
- Identify the universal set
- Find intersection, unions, and complements of sets
- Model relationships between sets using Venn diagrams
- Recognize and be able to apply cardinality notation
- Use cardinality notation and formulas to solve Venn diagrams
Summary of Set Theory Symbols
|
Symbol |
Name |
Example |
Explanation |
|
{list of elements} |
Set |
A = {1, 3} B = {2, 3, 9} C = {3,9} |
Collection of distinct objects Curly brackets are used to designate a set |
|
∩ |
Intersection |
A ∩ B = {3} |
Belong to both set A AND set B |
|
∪ |
Union |
A ∪ B = {1,2,3,9} |
Belong to set A OR set B (or both) |
|
⊂ ⊃ |
Proper Subset |
1 ⊂ {1,2} C ⊂ B 1,2 ⊃ {1} |
A set that is contained in another set |
|
⊆ ⊇ |
Subset |
1 ⊆ A {1,3} ⊆ A |
A set that is contained in or equal to another set |
|
⊄
|
Not a proper subset |
{1,3} ⊄ A |
A set that is not contained in another set |
|
∈ |
Is a member or element |
3 ∈ A |
3 is an element in set A |
|
∉ |
Is not a member or element |
4 ∉ A |
4 is not an element in set A |
|
∅ or {} |
Empty Set |
{ } |
The set that contains no elements |
It is natural for us to classify items into groups, or sets, and consider how those sets overlap with each other. We can use these sets to understand relationships between groups, and to analyze survey data.
An art collector might own a collection of paintings, while a music lover might keep a collection of CDs. Any collection of items can form a set.
| Set |
|
A set is a collection of distinct objects, called elements of the set. A set can be defined by describing the contents. This is called verbal notation. A set can also be defined by listing the elements of the set, enclosed in curly brackets. This is known as roster notation. |
| Example 1 |
|
Some examples of sets that are defined by describing the contents of the set: a) The set of all even numbers b) The set of all books written about travel to Chile |
|
Some examples of sets that are defined by listing the elements of the set: a) {1, 3, 9, 12} b) {red, orange, yellow, green, blue, indigo, purple} |
| Notation |
|
We will use a variable to represent a set, to make it easier to refer to that set later. The symbol ∈ means “is an element of”. A set that contains no elements, { }, is called the empty set and can also be written ∅. Caution: ∅ is not the zero symbol, “0”. It is an abbreviation for the empty set. |
| Example 2 |
|
Let A = {1, 2, 3, 4} To notate that 2 is an element of the set, we write 2 ∊ A |
Set Interactions
It is very common for sets to interact. For example, you and a new roommate decide to have a house party, and you both invite your circle of friends. At this party, two sets are being combined, though it might turn out that there are some friends that were in both sets.
| Union, Intersection, and Complement |
|
The union of two sets contains all the elements contained in either set A, or set B, or in both sets. The union is written “A ⋃ B” or “A or B”. The intersection of two sets contains only the elements that are in both sets A and B. The intersection is written “A ⋂ B” or “A and B”. The complement of a set A contains everything that is not in the set A. The complement of A can be written Ac, A̅, A’, not A, or sometimes ~A. For consistency, this text will use A̅. |
For the house party described above, the union is the set of all your friends along with the friends of your roommate or all the friends together.
The intersection will be the friends that you and your roommate share in common.
| Example 3 |
|
Consider the sets: A = {red, green, blue} B = {red, yellow, orange} C = {red, orange, yellow, green, blue, purple} D = {yellow, white} a) Find A ⋃ B The union contains all the elements in either set A or set B, or both: A ⋃ B = {red, green, blue, yellow, orange} b) Find A ⋂ B The intersection contains all the elements in both sets: A ⋂ B = {red} c) Find A̅ ⋂ C Here we are looking for all the elements that are not in set A and are also in C. To solve this problem, write out all the elements of set C, then remove the elements that are also contained in set A. A̅ ⋂ C = {orange, yellow, purple} d) Find A ⋂ D. Because set A and set D have no elements in common, we can write: A ⋂ D = ∅ or A ⋂ D = { } |
| You Try PC.0.A |
|
Using the sets from the previous example, find A ⋃ C and B̅ ⋂ A. |
Notice that in the example above, it would be hard to just ask for A̅ since everything from the color fuchsia to puppies and peanut butter are included in the complement of the set. For this reason, complements are usually only used with intersections, or when we have a universal set in place.
| Universal Set |
|
A universal set is a set that contains all the elements we are interested in. A complement is relative to the universal set, so A̅ contains all the elements in the universal set that are not in A. |
| Example 4 |
| a. If we were discussing searching for books, the universal set might be all the books in the library.
b. If we were grouping your Facebook friends, the universal set would be all your Facebook friends. c. If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers. d. If you were working with letters, the universal set might include all 26 letters in the English alphabet. |
| Example 5 |
|
Suppose the universal set is U = all whole numbers from 1 to 9. If A = {1, 2, 4}, then A̅ = {3, 5, 6, 7, 8, 9} |
| You Try SV.2.B |
|
Suppose the universal set is U = all odd numbers from 1 to 15. If A = {1, 3, 9, 11}, then A̅ = ______________________________ |
| Set Operations |
As we saw earlier with the expression A̅ ⋂ C, set operations can be grouped together. Grouping symbols can be used like they are with arithmetic, which is to force the order of operations.
Rules for set operations:
- Work from left to right.
- Set operations within parenthesis should be done first.
- If there is a complement inside the parenthesis, the complement should be done first.
| Example 6 |
|
Suppose H = {cat, dog, rabbit, mouse}, F = {dog, cow, duck, pig, rabbit}, W = {duck, rabbit, deer, frog, mouse} a. Find (H ⋂ F) ⋃ W We start with the intersection: H ⋂ F = {dog, rabbit} Now we union that result with W: (H ⋂ F) ⋃ W = {dog, duck, rabbit, deer, frog, mouse} b. Find H ⋂ (F ⋃ W) We start with the union: F ⋃ W = {dog, cow, rabbit, duck, pig, deer, frog, mouse} Now we intersect that result with H: H ⋂ (F ⋃ W) = {dog, rabbit, mouse} c. Find [latex]\overline{(H~\cap~F)}~\cap~W[/latex] We start with the intersection: H ⋂ F = {dog, rabbit} Now we want to find the elements of W that are not in H ⋂ F [latex]\overline{(H~\cap~F)}~\cap~W[/latex] = {duck, deer, frog, mouse} Note: You normally need to know the universal set to find the complement of a set. However, in this problem we were able to determine the answer by thinking about the meaning of the set operations. |
Venn Diagrams
To visualize the interaction of sets, John Venn in 1880 thought to use overlapping circles, building on a similar idea used by Leonhard Euler in the 18th century. These illustrations are now called Venn Diagrams.
| Venn Diagram |
|
A Venn diagram represents each set by a circle, usually drawn inside of a rectangle. The rectangle represents the universal set. Overlapping areas of circles indicate elements common to both sets. Note: There is no meaning to the size of the circle. Basic Venn diagrams can illustrate the interaction of two or three sets. |
| Example 7 | |
|
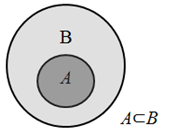
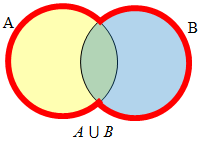
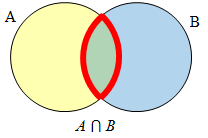
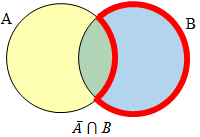
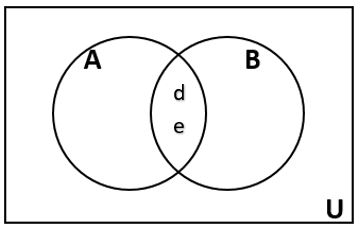
Create Venn diagrams to illustrate A ⊂ B , A ⋃ B, A ⋂ B, and A̅ ⋂ B |
|
|
A ⊂ B means that A is a proper subset of set B. So all elements in set A are also elements in Set B.
|
A ⋃ B contains all elements in either set. The elements can be in set A or set B or both.
|
|
A ⋂ B contains only those elements in both sets – in the overlap of the circles. The elements are in set A and set B.
|
A̅ will contain all elements not in the set A.
A̅ ⋂ B will contain the elements in set B that are not in set A.
|
| Example 8 |
|
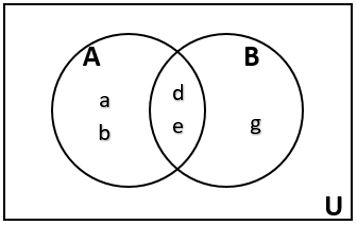
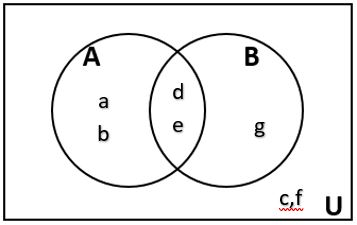
Draw a Venn Diagram to represent the sets U = {a, b, c, d, e, f, g}, A = {a, b, d, e}, and B = {d, e, g}. |
| We’ll start by identifying all the elements in the set A ⋂ B. This means all the elements in set A and set B.
Now, write the remaining elements of A inside the region A but outside the intersection of A and B. Do the same for the remaining elements of B.
Now, complete the Venn Diagram by writing any elements from the universal set that were not in A or B.
|
Cardinality
Often we are interested in the number of items in a set or subset. This is called the cardinality of the set.
| Cardinality |
|
The number of elements in a set is the cardinality of that set. The cardinality of the set A is often notated as n(A). |
| Example 9 |
|
Let A = {1, 2, 3, 4, 5, 6} and B = {2, 4, 6, 8}. Find the following: n(B ) n(A ⋃ B ) n(A ⋂ B ) |
|
n(B ) = 4, since there are 4 elements in the set. Since A ⋃ B = {1, 2, 3, 4, 5, 6, 8}, which contains 7 elements, n(A ⋃ B ) = 7. Since A ⋂ B = {2, 4, 6}, which contains 3 elements, n(A ⋂ B ) = 3 |
| Example 10 |
|
Find n(P), where P = the set of English names for the months of the year? |
|
n(P) = 12, since there are 12 months in the year. |
| Example 11 |
|
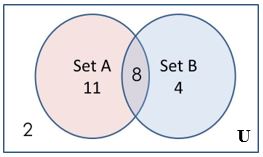
Consider the Venn diagram below
Determine [latex]n(A)[/latex], [latex]n(\bar{B})[/latex], [latex]n(\bar{A})[/latex], [latex]n(A~\cup~B)[/latex], [latex]n(B)[/latex], [latex]n(A~\cap~\bar{B})[/latex]
|
|
[latex]n(A)[/latex] = 11 + 8 = 19 [latex]n(\bar{B})[/latex] = 11 + 2 = 13 [latex]n(\bar{A})[/latex] = 2 + 4 = 6 [latex]n(A~\cup~B)[/latex] = 11 + 8 + 4 = 23 [latex]n(B)[/latex] = 8 + 4 = 12 [latex]n(A~\cap~\bar{B})[/latex] = 11 |
Sometimes (as in the previous example) we may be interested in the cardinality of the union or intersection of sets, but not know the actual elements of each set. This is common in surveying applications like the ones below. To help solve problems like this we will often draw Venn diagrams where we label the regions with the number of elements in it (as in the previous example). When you read a Venn diagram it is important identify if it is illustrating the cardinality of the regions or the elements of the region. You will be able to tell from the context of the problem.
| Example 12 |
|
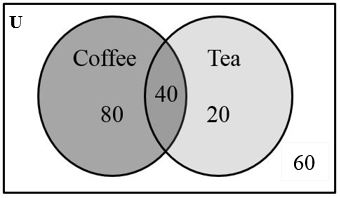
A survey asks a number of people “What beverage do you drink in the morning?”, and offers choices:
a. How many people drink tea in the morning? b. How many people drink nether tea no coffee? c. How many people drink coffee or tea in the morning? d. How many people were surveyed? |
|
a. How many people drink tea in the morning? 40 + 20 = 60 people drink tea in the morning b. How many people drink nether tea nor coffee in the morning? 60 people drink neither tea nor coffee in the morning c. How many people drink coffee or tea in the morning? 80 + 40 + 20 = 140 people drink coffee or tea in the morning d. How many people were surveyed? 80 + 40 + 20 + 60 = 200 people were surveyed |
| Example 13 |
|
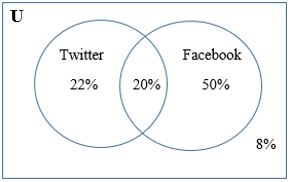
A survey asks which online services have you used in the last month:
a. What percentage of people have used Twitter but not Facebook? b. Determine the percentage of people who used Facebook? |
| a. What percentage of people have used Twitter but not Facebook?
b. Determine the percentage of people who used Facebook? |
| You Try PC.0.C |
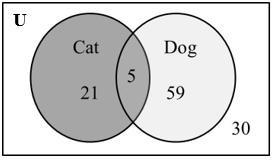
| In a survey, pet owners were asked if they had a dog or cat or both. The results of the survey are displayed in this Venn Diagram:
Use the Venn Diagram to determine: a. How many of the pet owners surveyed owned neither a cat nor a dog? b. How many of the pet owners surveyed owed a dog? c. How many of the pet owners surveyed owed a dog or a cat? d. How many of the pet owners surveyed owed only a dog? e. How many of the pet owners surveyed owed a cat but not a dog? f. How many people were surveyed? |
| Example 14 |
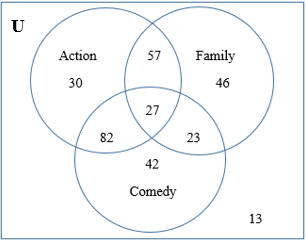
| A group of adults was surveyed about the types of movies they enjoyed watching.
Do you enjoy watching action movies? Do you enjoy watching family movies? Do you enjoy watching comedy movies? The results were as follows:
a. How many adults were surveyed? b. How many of those surveyed enjoy action movies? c. How many of those surveyed enjoy all three? d. How many of those surveyed enjoyed family, but not comedy or action movies? e. How many of those surveyed enjoy comedy movies and action movies? f. How many of those surveyed enjoy comedy movies or family movies? g. How many of those surveyed did not enjoy comedy movies? |
| a. How many adults were surveyed?
30 + 57 + 46 + 82 + 27 + 23 + 42 + 13 = 320 b. How many of those surveyed enjoy action movies? 30 + 57 + 27 + 82 = 196 c. How many of those surveyed enjoy all three? 27 d. How many of those surveyed enjoyed family, but not comedy or action movies? 46 e. How many of those surveyed enjoy comedy movies and action movies? 82 + 27 = 109 f. How many of those surveyed enjoy comedy movies or family movies? 57 + 46 + 27 + 23 + 82 + 42 = 277 g. How many of those surveyed did not enjoy comedy movies? 30 + 57 + 46 + 13 = 146 |
| Example 15 |
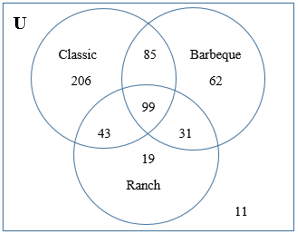
| In a survey of 556 adults about consumer preferences for flavors of potato chips, the following results were obtained:
a. How many people were surveyed? Of those surveyed: b. How many people did not prefer any of the three flavors? c. How many people prefer ranch and barbeque but not classic? d. How many people prefer barbeque or classic? e. How many people prefer only ranch? f. How many people prefer barbeque but not classic? g. How many people prefer classic or ranch, but not barbeque? |
| a. How many people were surveyed?
206 + 85 + 62 + 43 + 99 + 31 + 19 + 11 = 556 Of those surveyed: b. How many people did not prefer any of the three flavors? 11 c. How many people prefer ranch and barbeque but not classic? 31 d. How many people prefer barbeque or classic? 206 + 85 + 62 + 43 + 99 + 31 = 526 e. How many people prefer only ranch? 19 f. How many people prefer barbeque but not classic? 62 + 31 = 93 g. How many people prefer classic or ranch, but not barbeque? 206 + 43 + 19 = 268 |
Section PC.0 – Answers to You Try Problems
PC.0.A
[latex]A~\cup~C[/latex] = {red, orange, yellow, green, blue, purple}
[latex]\bar{B}~\cap~A[/latex] = {green, blue}
PC.0.B
[latex]\bar{A}[/latex] = {5, 7, 13, 15}
PC.0.C
a. 30
b. 64
c. 85
d. 59
e. 21
f. 115