Section PC.0 – Practice Problems

1. Use the roster method to list the elements of the set: The letters of the word “Mississippi”.

2. Use the roster method to list out the elements of the set “Months of the year".

3. Suppose the universal set is U = {1, 2, 3, … , 8, 9, 10}. If [latex]A[/latex] = {5, 6, 8}, find [latex]\bar{A}[/latex].

4. Suppose the universal set is U = {red, orange, yellow, green, blue, purple}. If [latex]A[/latex] = {red, green, blue}, find [latex]\bar{A}[/latex].

5. Suppose the universal set U is all even numbers from 2 to 20. If [latex]A[/latex] = {4, 6, 10, 16, 18, 20}, find [latex]\bar{A}[/latex].

6. Let U = {1, 2, 3, … , 18, 19, 20} be the universal set. Consider the sets:

[latex]A[/latex] = {2, 3, 5, 7, 10, 11, 12, 13, 14, 16, 17, 19}

[latex]B[/latex] = {5, 10, 13, 14, 16, 19, 20}

Find the following:

• a. [latex]A~\cup~B[/latex]
• b. [latex]A~\cap~B[/latex]
• c. [latex]\bar{A}~\cap~B[/latex]

7. Let U = {1, 2, 3, … , 18, 19, 20} be the universal set. Consider the sets:

[latex]A[/latex] = {6, 11, 12, 14, 16, 17, 18}

[latex]B[/latex] = {1, 4, 5, 8, 11, 12, 15, 16}

Find the following:

• a. [latex]A~\cup~B[/latex]
• b. [latex]A~\cap~B[/latex]
• c. [latex]A~\cap~\overline{B}[/latex]

8. Let U = {1, 2, 3, ... , 18, 19, 20} be the universal set. Consider the sets:

[latex]A[/latex] = {1, 2, 3, 4, 6, 8, 9, 11, 12, 14, 15, 18}

[latex]B[/latex] = {5, 9, 12, 14, 17, 19, 20}

Find the following:

• a. [latex]A~\cup~B[/latex]
• b. [latex]A~\cap~B[/latex]
• c. [latex]\bar{A}~\cap~B[/latex]

9. Let U = {1, 2, 3, … , 8, 9, 10} be the universal set. Consider the sets:

[latex]A[/latex] = {3, 5, 8, 10}

[latex]B[/latex] = {1, 3, 4, 7, 8, 9, 10}

[latex]C[/latex] = {2, 5, 6}

Find the following:

• a. [latex]A~\cup~C[/latex]
• b. [latex]B~\cap~C[/latex]
• c. [latex]A~\cap~\overline{B}[/latex]
• d. [latex]\overline{(A~\cup~C)}[/latex]

10. Let D = {b, a, c, k}, E = {t, a, s, k}, F = {b, a, t, h}, and U = set of letters in the alphabet. Using these sets, find the following:

• a. [latex]\bar{D}~\cap~E[/latex]
• b. [latex]\bar{F}~\cap~D[/latex]

11. Create a Venn diagram to illustrate each of the following:

• a. [latex]\bar{C}[/latex]
• b. [latex]A~\cup~B[/latex]
• c. [latex]A~\cap~B[/latex]
• d. [latex]A~\cup~\overline{B}[/latex]

12. Use the Venn diagram to write each of the sets below in roster form.

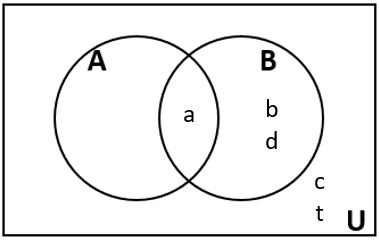
• a. [latex]\bar{A}~\cap~B[/latex]
• b. [latex]\overline{B}~\cup~A[/latex]

13. Let A = {1, 2, 3, 4, 5}   B = {1, 3, 5}   C = {4, 6}

Find the following:

• a. The cardinality of [latex]A[/latex]
• b. The cardinality of [latex]B[/latex]
• c. The cardinality of [latex]A~\cup~C[/latex]
• d. The cardinality of [latex]A~\cap~C[/latex]

14. Let A = {1, 5, 9}   B = {1, 2, 3, 4, 5, 6, 8}   C = {2, 4, 5, 8, 9}

Find the following:

• a. [latex]n(A)[/latex]
• b. [latex]n(B)[/latex]
• c. [latex]n(C)[/latex]
• d. [latex]n(B~\cap~C)[/latex]
• e. [latex]n(A~\cup~C)[/latex]

15. Consider the Venn diagram below.

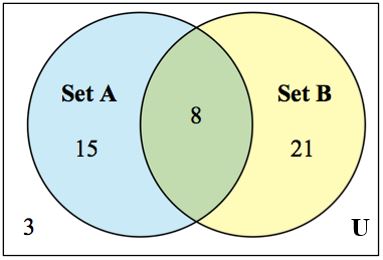
Find the following:

• a. [latex]n(A)[/latex]
• b. [latex]n(\bar{A})[/latex]
• c. [latex]n(B)[/latex]
• d. [latex]n(\overline{B})[/latex]
• e. [latex]n(A~\cap~B)[/latex]
• f. [latex]n(A~\cup~B)[/latex]
• g. [latex]n(\bar{A}~\cap~B)[/latex]

16. Consider the Venn diagram below.

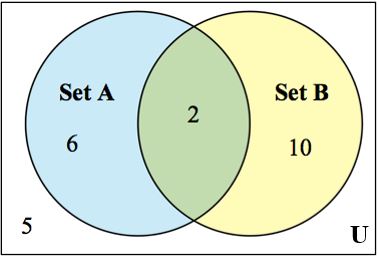
Find the following:

• a. [latex]n(A)[/latex]
• b. [latex]n(\bar{A})[/latex]
• c. [latex]n(B)[/latex]
• d. [latex]n(\overline{B})[/latex]
• e. [latex]n(A~\cap~B)[/latex]
• f. [latex]n(A~\cup~B)[/latex]
• g. [latex]n(\bar{A}~\cap~\overline{B})[/latex]

17. Consider the Venn diagram below.

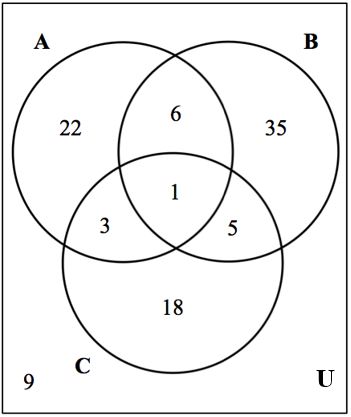
Find the following:

• a. [latex]n(A)[/latex]
• b. [latex]n(C)[/latex]
• c. [latex]n(\overline{B})[/latex]
• d. [latex]n(A~\cap~C)[/latex]
• e. [latex]n(B~\cup~C)[/latex]
• f. [latex]n((B~\cap~C)~\cup~A)[/latex]

18. The following Venn diagram shows students in various college courses.

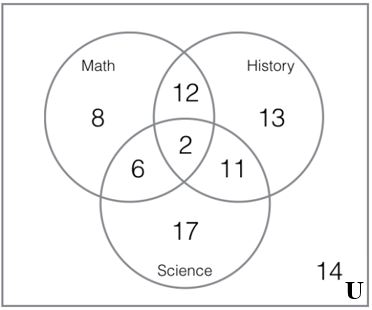
Find the following:

• a. How many students are taking Math?
• b. How many students are taking Math and Science?
• c. How many students are taking History and Science, but not Math?
• d. How many students are taking exactly two of these classes?

19. How many students are taking exactly two of these classes.

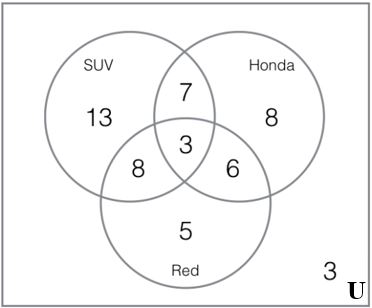
Find the following:

• a. How many Hondas are in the parking lot?
• b. How many red SUVs are in the parking lot?
• c. How many of the Red cars in the parking lot are not Hondas?

20. The following Venn diagram shows people at a party.

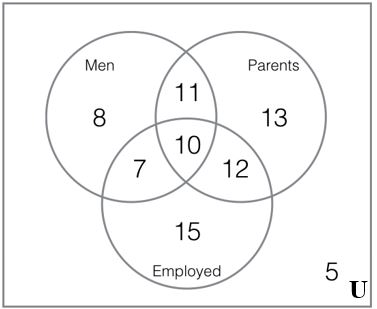
Find the following:

• a. How many people at the party are employed?
• b. How many people at the party are mothers?
• c. How many people at the party are working fathers?
• d. How many people at the party are not parents?