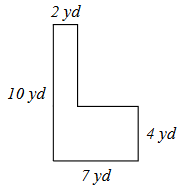Module G: Fundamentals of Geometry
Module G Learning Objectives:
- Recognize the difference between one, two, and three-dimensional objects
- Be able to find perimeter and area of standard and composite shapes
- Calculate the length of any side of a right triangle
- Find the area and circumference of a circle
- Find the volume of standard 3-Dimensional shapes
- Find the surface area of standard 3-Dimensional shapes
- Apply the geometric formulas to problem solve
Section G.1 – Geometry Basics & Perimeter
Section G.2 – Area
Section G.3 – Triangles: The Pythagorean Theorem & Similarity
Section G.4 – Circles
Section G.5 – Perimeter and Area of Composite Figures
Section G.6 – Working in Three Dimensions: Volume and Surface Area
Section G.1 – Geometry Basics and Perimeter
Geometric terms are used in everyday language, often without thinking about it. For example, any time you say “walk along this line” or “watch out, this road quickly angles to the left” you are using geometric terms to make sense of the environment around you. You use these terms flexibly, and people generally know what you are talking about.
In the world of mathematics, each of these geometric terms has a specific definition. It is important to know these definitions – as well as how different figures are constructed – to become familiar with the language of geometry. Let’s start with the most basic geometric idea: a point.
A point is simply a location, which has no dimensions! That might seem strange, but the geometric idea of a point is that it has no length, no width, and no height. The easiest way to visualize this is by imagining sticking the tip of a pin into a map. The pinpoint is serving to mark a location, not to measure an amount of space taken up by the tip of the pin itself.
While a point is a simple idea in geometry, it is a building block for more difficult geometric figures. Considering more than one point helps to build dimension in geometry. By considering any two distinct points, we now can form a line connecting the two points. A line is a one-dimensional figure (it has length, but no width and no height) that is made up of an infinite number of individual points placed side by side. In geometry all lines are assumed to be straight; if they are not straight they are called a curve. A line continues infinitely (forever) in two directions, usually indicated by placing arrows at the two ends. A line segment does not continue infinitely in two directions, but has two endpoints, usually indicated by placing points at the two ends.

Putting it all Together: Figures on a Plane
A plane is a flat surface that continues forever (or, in mathematical terms, infinitely) in every direction. It has two dimensions: length and width. You can visualize a plane by placing a piece of paper on a table. Now imagine that the piece of paper stays perfectly flat and extends as far as you can see in four directions, left-to-right and front-to-back. This gigantic piece of paper gives you a sense of what a geometric plane is like: it continues infinitely in two dimensions. (Unlike the piece of paper example, though, a geometric plane has no height.)
A plane can contain a number of geometric figures, some of which we have already mentioned. Recall the most basic geometric idea is a point, which has no dimensions. A point is simply a location on the plane. It is represented by a dot. If we increase from one point on a plane to two points on a plane, we have a one-dimensional line. As we increase again, this time from 2 points to 3 points (that are not all on the same straight line), we now define the plane itself.
Perimeter
The perimeter of a two-dimensional shape is the distance around the shape. You can think of wrapping a string around the 3 sides of a triangle. The length of this string would be the perimeter of the triangle. Or walking around the outside of a park, you walk the distance of the park’s perimeter. Some people find it useful to think “peRIMeter” because the edge of an object is its rim and peRIMeter has the word “rim” in it.
If the shape is a polygon–a closed, two-dimensional shape with straight sides– then you can add up all the lengths of the sides to find the perimeter. Be careful to make sure that all the lengths are measured in the same units. You measure perimeter in linear units, which is one dimensional. Examples of units of measure for length are inches, centimeters, or feet.
| Example 1 | |
|
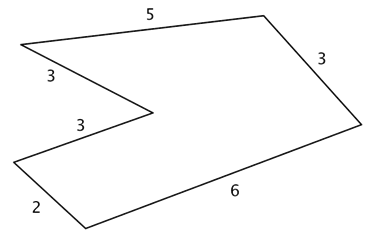
Find the perimeter of the given figure. All measurements indicated are inches.
|
|
|
P = 5 + 3 + 6 + 2 + 3 + 3 |
Since all the sides are measured in inches, just add the lengths of all six sides to get the perimeter. |
|
P = 22 inches (Remember to include units.) |
This means that a tightly wrapped string running the entire distance around the polygon would measure 22 inches long. |
Sometimes, you need to use what you know about a polygon in order to find the perimeter. Let’s look at the rectangle in the next example.
| Example 2 | |
|
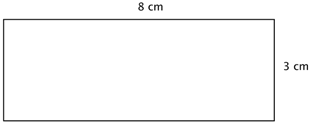
A rectangle has a length of 8 cm and a width of 3 cm. Find the perimeter.
P = 3 + 3 + 8 + 8 P = 22 cm Since this is a rectangle, the opposite sides have the same lengths, 3 cm. and 8 cm. Add up the lengths of all four sides to find the perimeter. |
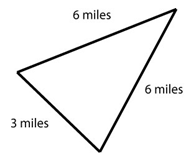
Find the perimeter of each of the figures shown below. Be sure to include correct units in your answers. A)
B)
|
Section G.1 – Answers to You Try Problems
G.1.A
a. 15 miles
b. 34 yards