Section G.2 - Area
The area of a two-dimensional figure describes the amount of surface the shape covers. You measure area in square units of a fixed size. Examples of square units of measure are square inches, square centimeters, or square miles. When finding the area of a polygon, you count how many squares of a certain size will cover the region inside the polygon.
| Example 1 | |
|
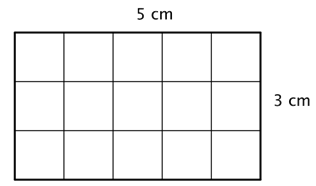
Find the area of the rectangle below.
|
You can count the squares individually, but it is much easier to multiply 3 times 5 to find the number more quickly. And, more generally, the area of any rectangle can be found by multiplying length times width. The area of the rectangle with length 5cm and width 3cm would be: 5cm • 3cm = 15cm2 |
To help you find the area of the many different categories of polygons, mathematicians have developed formulas. These formulas help you find the measurement more quickly than by simply counting. The formulas you are going to look at are all developed from the understanding that you are counting the number of square units inside the polygon.
|
Shape |
Area |
|
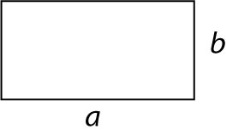
Rectangle with side lengths a, b
|
A = a • b |
|
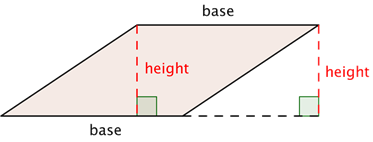
Parallelogram with height h and base b
|
A = b • h
|
|
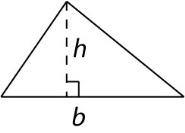
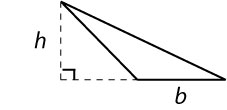
Triangle with height h and base b
|
A = [latex]\frac{1}{2}bh[/latex] = [latex]\frac{bh}{2}[/latex] |
|
Trapezoid as shown below
|
A = [latex]\frac{b_1~+~b_2}{2}h[/latex]
|
|
Example 2 |
||
|
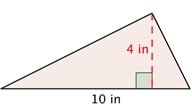
A triangle has a height of 4 inches and a base of 10 inches. Find the area. |
||
|
|
A = [latex]\frac{1}{2}[/latex]bh |
Start with the formula for the area of a triangle. |
|
A = [latex]\frac{1}{2}[/latex](10)(4) |
Substitute 10 for the base and 4 for the height. |
|
|
A = 20 in2 |
||
|
Example 3 |
|
|
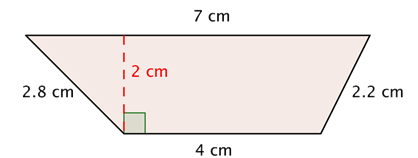
Find the area and perimeter of the trapezoid shown below.
AREA |
|
|
A = [latex]\frac{b_1~+~b_2}{2}[/latex]h A = [latex]\frac{4~+~7}{2}[/latex] • 2 A = [latex]\frac{11}{2}[/latex] • 2
A = 11
|
Start with the formula for the area of a trapezoid. Substitute 4 and 7 for the bases and 2 for the height, and find A. The area of the trapezoid is 11 cm2. |
|
PERIMETER |
|
|
Remember that perimeter is the distance around a closed shape. P = 7 cm + 2.2 cm + 4 cm + 2.8 cm = 16 cm |
|
|
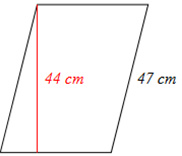
You Try 6.2.A Find the perimeter and area of the parallelogram shown below. |
Section G.2 – Answers to You Try Problems
G.2.A
Perimeter = 164 cm
Area = 1540 cm2