Section G.5 – Perimeter and Area of Composite Figures
Often you need to find the area or perimeter of a shape that is not a standard polygon. Artists and architects, for example, usually deal with complex shapes. However, even complex shapes can be thought of as being composed of smaller, less complicated shapes, like rectangles, trapezoids, and triangles.
To find the perimeter of non-standard shapes, you still find the distance around the shape by adding together the length of each side. Finding the area of non-standard shapes is a bit different. You need to create regions within the shape for which you can find the area, and add these areas together. Have a look at how this is done below.
| Example 1 | |
|
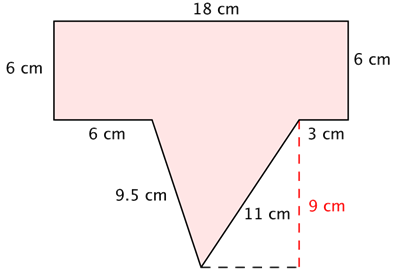
Find the perimeter of the polygon.
PERIMETER |
|
|
P = 18 + 6 + 3 + 11 + 9.5 + 6 + 6 P = 59.5 cm
|
To find the perimeter, add together the lengths of the sides. Start at the top and work clockwise around the shape. The perimeter of this shape is 59.5cm. |
|
|
|
| Example 2 | |
|
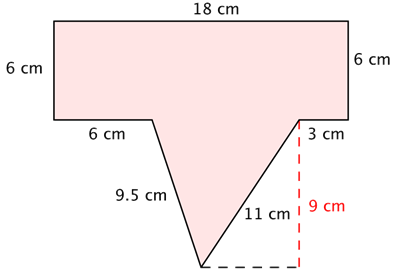
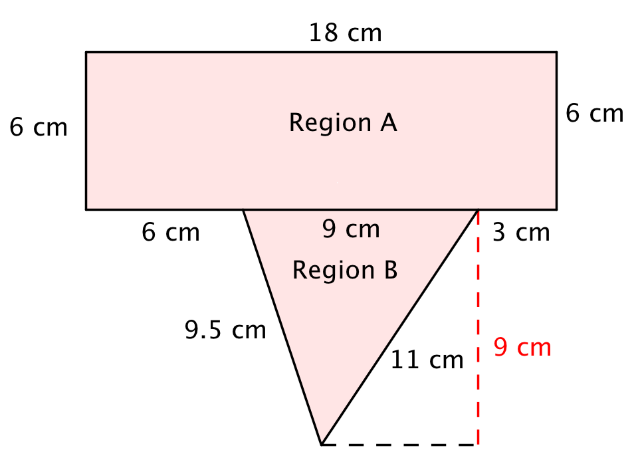
Find the area of the polygon.
AREA |
|
|
Area of Polygon = (Area of A) + (Area of B) |
To find the area, divide the polygon into two separate, simpler regions. The area of the entire polygon will equal the sum of the areas of the two regions. |
|
Region A is a rectangle. To find the area, multiply the length (18) by the width (6). A = L • W = 18 • 6 = 108 The area of Region A is 108 cm2. |
|
|
Region B is a triangle. To find the area, use the formula [latex]\frac{1}{2}[/latex]bh, where the base is 9 and the height is 9. A = [latex]\frac{1}{2}[/latex]bh = [latex]\frac{1}{2}[/latex](9)(9) = 40.5 The area of Region B is 40.5 cm2. |
|
|
Add the regions together to find the total area: 108 cm2 + 40.5 cm2 = 148.5 cm2 |
|
You also can use what you know about perimeter and area to help solve problems about situations like buying fencing or paint, or determining how big a rug is needed in the living room. Here’s a fencing example.
| Example 3 | |
|
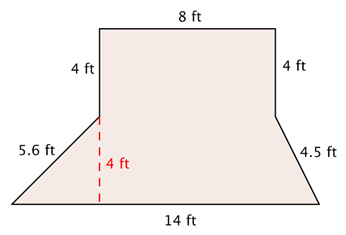
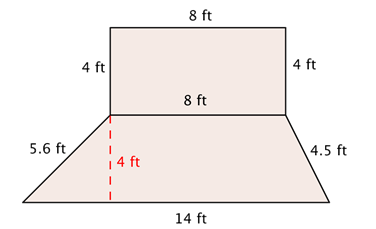
Rosie is planting a garden with the dimensions shown below. She wants to put a thin, even layer of mulch over the entire surface of the garden. The mulch costs $3 a square foot. How much money will she have to spend on mulch?
|
|
|
This shape is a combination of two simpler shapes: a rectangle and a trapezoid. |
|
|
Find the area of the trapezoid. A = [latex]\frac{b_1~+~b_2}{2}[/latex]h A = [latex]\frac{14~+~8}{2}[/latex] • 4 A = [latex]\frac{22}{2}[/latex] • 4 A = 44 ft2 |
Find the area of the rectangle. A = L • W A = 8 • 4 A = 32 ft2
|
|
Add the measurements. 32 ft2 + 44 ft2 = 76 ft2 |
|
|
Multiply by $3 to find out how much Rosie will have to spend. 76 ft2 • $3 = $228 |
|
|
Rosie will spend $228 to cover her garden with mulch. |
|
|
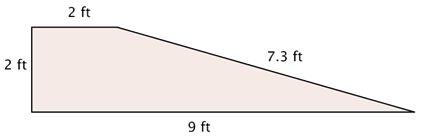
You Try G.5.A Find the perimeter and area of the shape shown below. Be sure to use correct units in your answer.
|
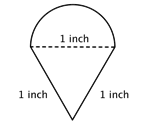
Since you also know how to calculate the circumference and area of a circle, you can use this knowledge to find the perimeter and area of composite figures that include circles and semi-circles. The trick to figuring out these types of problems is to identify shapes (and parts of shapes) within the composite figure, calculate their individual dimensions, and then add them together. For example, look at the image below. Is it possible to find the perimeter?
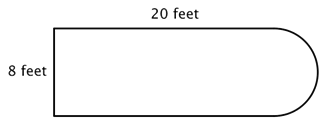
The first step is to identify simpler figures within this composite figure. You can break it down into a rectangle and a semicircle, as shown below.
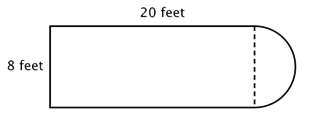
You know how to find the perimeter of a rectangle, and you know how to find the circumference of a circle. Here, the perimeter of the three solid sides of the rectangle is 8 + 20 + 20 = 48 feet. (Note that only three sides of the rectangle will add into the perimeter of the composite figure because the other side is not at an edge; it is covered by the semicircle!)
To find the circumference of the semicircle, use the formula C = πd with a diameter of 8 feet, then take half of the result. The circumference of the semicircle is 4π, or approximately 12.56 feet.
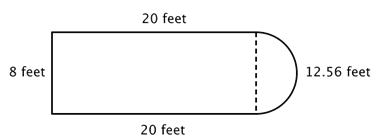
Adding up the sides, we find that the total perimeter is about 60.56 feet.
| Example 4 | ||
|
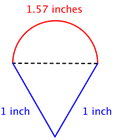
Find the perimeter (to the nearest hundredth) of the composite figure, made up of a semi-circle and a triangle.
|
||
|
Identify smaller shapes within the composite figure. This figure contains a semicircle and a triangle. Since we are looking for the perimeter, we need to first find the circumference of the semicircle. |
||
|
Find the circumference of the circle. Then divide |
Diameter (d) = 1 C = πd |
|
|
Circumference of semicircle = [latex]\frac{1}{2}[/latex]π or approximately 1.57 inches Find the total perimeter by adding the circumference of the semicircle and the lengths of the two legs. Since our measurement of the semi-circle’s circumference is approximate, the perimeter will be an approximation also. |
||
|
|
Perimeter = 1 + 1 + 12π ≈ 3.57 inches The perimeter is approximately 3.57 inches |
|
| Example 5 | ||
|
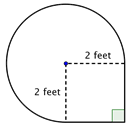
Find the area of the composite figure, made up of three-quarters of a circle and a square, to the nearest hundredth.
|
||
|
Identify smaller shapes within the composite figure. This figure contains a circular region and a square. If you find the area of each, you can find the area of the entire figure. |
||
|
Find the area of the square.
|
A = s2 A = (2)2 A = 4 ft2 |
|
|
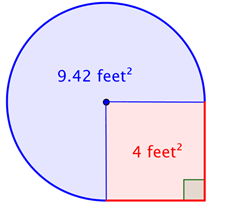
Find the area of the circular region. The radius is 2 feet. Note that the region is ¾ of a whole circle, so you need to multiply the area of the circle by ¾. Area of full circle: A = πr2 Area of ¾ of full circle: ¾(4π) = 3π This is approximately 9.42 ft2 |
||
|
Add the two regions together. Since your measurement of the circular’s area is approximate, the area of the figure will be an approximation also. 4 feet2 + 3π feet2 = approximately 13.42 feet2 The total area is approximately 13.42 feet2. |
|
|
|
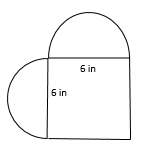
You Try G.5.B Find the perimeter and area of the shape shown below. Be sure to use correct units in your answers. Round your answers to the nearest hundredth as needed. Be sure to include correct units in your answers. (Both rounded regions are semi-circles.)
|
Section G.5 – Answers to You Try Problems
G.5.A
Perimeter = 20.3 feet
Area = 11 square feet
G.5.B
Perimeter = 30.85 in
Area = 64.27 in2