Section G.6 – Practice Problems
Round your answers to two decimal places unless otherwise noted.
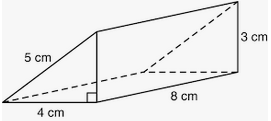
1. Find the volume of the figure below.
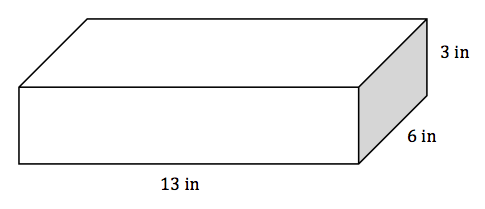
2. Find the volume of the figure below.
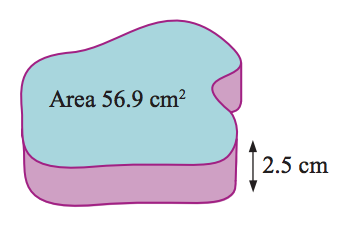
3. Find the volume of the figure below.
4. Sketch a cylinder with radius of 10 feet and height of 4 feet. Find the volume (round to the nearest tenth).
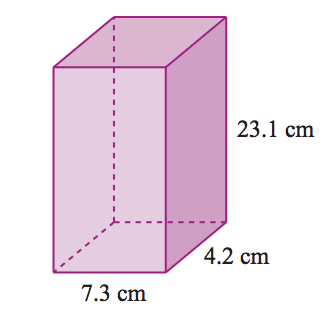
5. Find the volume of the figure below.
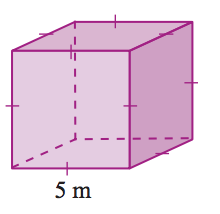
6. Find the volume of the figure below.
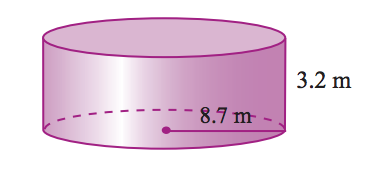
7. Find the volume of the figure below.
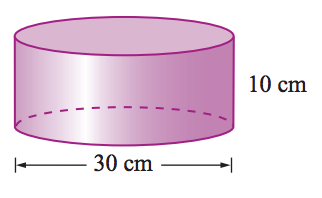
8. Sketch a cone with radius of 7 feet and height of 8 feet. Find the volume (round to the nearest tenth).
9. A rectangular swimming pool has a length of 13 feet, a width of 24 feet, and a depth of 5 feet. How many cubic feet of water can the pool hold?
10. A sports ball has a diameter of 30 cm. Find the volume of the ball (round to the nearest hundredth).
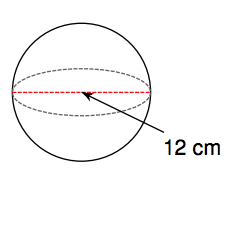
11. Find the volume of the figure below.
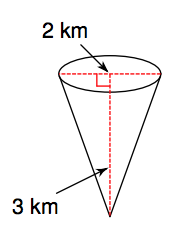
12. Find the volume of the figure to the right.
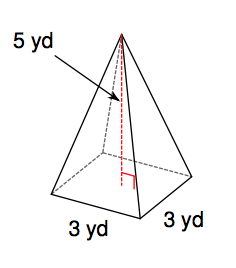
13. Find the volume of the figure to the right.
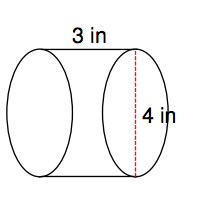
14. Find the volume of the figure to the right.
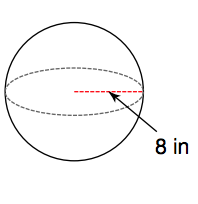
15. Find the volume of the figure to the right.
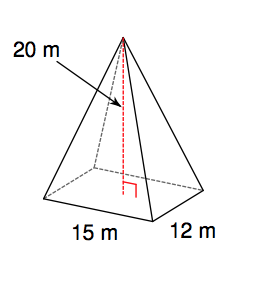
16. Find the volume of the figure to the right.
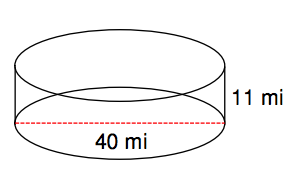
17. Find the volume of the figure below.
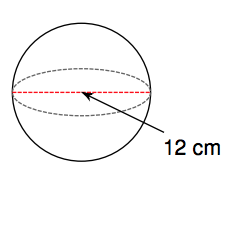
18. Callie is sending her nephew a soccer ball for his birthday. She packs the ball in a cubic box that has the same side length as the diameter of the ball. She needs to determine how much space needs to be filled with packing material. (Use 3.14 or the pi button on your calculator. Round all to the nearest hundredth.) If the sides of the box are 22 cm:
a. What is the volume of the box?
b. What is the volume of the ball?
c. What is the remaining volume of the box that needs to be filled with packing material?
19. Sylvia has just discovered that the valve on her cement truck failed during the night and that all the contents ran out to form a giant cone of hardened cement. To make an insurance claim, she needs to figure out how much cement is in the cone. The circumference of its base is 44 feet, and it is 4 feet high. Calculate the volume to nearest cubic foot.
20. Eight wooden spheres with radii of 3 inches are packed snugly into a square box 12 inches on one side. The remaining space is filled with packing beads. What is the volume occupied by the packing beads?
21. The water pipe has a radius of 5 cm and a height of 7 cm. What volume of water does it take to fill the pipe?
22. A baseball has a 45 cm diameter. What is the volume of the contents of the ball?
23. For Anya’s birthday her father gave out colorful birthday hats that were cone shaped. The opening of the bottom of the hat was 3 cm across (the diameter) and the height of the cone was 7 cm. Anya fills her hat with candy. What is the approximate volume of candy?
24. This cylindrical fish tank has a height of 36 inches and a diameter of 30 inches. What is the volume of the fish tank in cubic inches and in cubic feet? (1 cubic foot = 1728 cubic inches)
25. A rectangular prism has a base with a length of 25”, a width of 9” and a height of 12”. A second prism has a square base with a side of 15”. If the volumes of the two prims are equal, what is the height of the second prism?
26. Find the surface area of the figure below.
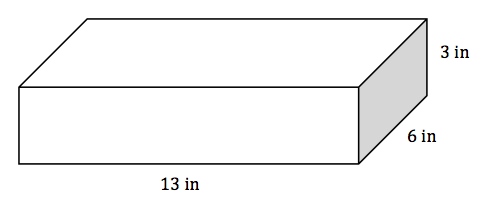
27. Find the surface area of the figure below. Write your answer in exact form and approximate form, rounded to the nearest hundredth using 3.14 for π.
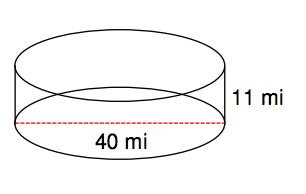
28. Find the surface area of the figure below. Write your answer in exact form and approximate form, rounded to the nearest hundredth using 3.14 for π.
29. A cylindrical water tower has a radius of 10 feet and a height of 20 feet. The outside of the water tower needs to be repainted. What is the total surface area of the water tower that will be repainted? Write your answer in exact form and approximate form, rounded to the nearest hundredth using 3.14 for π.
30. You are producing 500 of these metal wedges, and you must electroplate them with a thin layer of high-conducting silver (surface area). The measurements shown are in centimeters. Find the total cost for silver, if silver plating costs $1.21 for every square centimeter. Assume each non-triangular edge is a rectangle.