Section MU.2 – Length, Weight, and Capacity
Measurement is a number that describes the size or amount of something. You can measure many things like length, area, capacity, weight, temperature and time.
At times, you may need to convert between units of measurement. For example, you might want to express your height using feet and inches (5 feet 4 inches) or using only inches (64 inches). This process of converting from one unit to another unit is called unit analysis or dimensional analysis.
Length/Distance
Length is the distance from one end of an object to the other end, or from one object to another. For example, the length of a letter-sized piece of paper is 11 inches. The system for measuring length in the United States is based on the four customary units of length: inch, foot, yard, and mile. You can use any of these four U.S. customary measurement units to describe the length of something, but it makes more sense to use certain units for certain purposes. For example, it makes more sense to describe the length of a rug in feet rather than miles, and to describe a marathon in miles rather than inches.
The table below shows equivalents and conversion factors for the four customary units of measurement of length.
| Unit Equivalents | Conversion Factors (longer to shorter units of measurement) | Conversion Factors (shorter to longer units of measurement) |
| 1 foot (ft) = 12 inches (in) | [latex]\frac{12~inches}{1~foot}[/latex] | [latex]\frac{1~foot}{12~inches}[/latex] |
| 1 yard (yd) = 3 feet (ft) | [latex]\frac{3~feet}{1~yard}[/latex] | [latex]\frac{1~yard}{3~feet}[/latex] |
| 1 mile (mi) = 5,280 feet (ft) | [latex]\frac{5,280~ft}{1~mile}[/latex] | [latex]\frac{1~mile}{5,280~feet}[/latex] |
You can use the conversion factors to convert a measurement, such as feet, to another type of measurement, such as inches. Note that each of these conversion factors is a ratio of equal values, so each conversion factor equals 1. Multiplying a measurement by a conversion factor does not change the size of the measurement at all since it is the same as multiplying by 1; it just changes the units that you are using to measure.
There are many more inches for a measurement than there are feet for the same measurement, as feet is a longer unit of measurement. So, you could use the conversion factor [latex]\frac{1~yard}{3~feet}[/latex].
| Dimensional Analysis: The Factor-Label Method |
You can use the factor label method to convert a length from one unit of measure to another using the conversion factors. In the factor label method, you multiply by unit fractions to convert a measurement from one unit to another. Study the example below to see how the factor label method can be used to convert a measurement given in feet into an equivalent number of inches.
| Example 1 | ||||||||||||||
| How many inches are in [latex]3\frac{1}{2}[/latex] feet? | ||||||||||||||
There are 42 inches in [latex]3\frac{1}{2}[/latex] feet. |
Notice that by using the factor label method you can cancel the units out of the problem, just as if they were numbers. You can only cancel if the unit being cancelled is in both the numerator and denominator of the fractions you are multiplying. In the problem above, you cancelled feet and foot leaving you with inches, which is what you were trying to find.
What if you had used the wrong conversion factor?
[latex]\frac{7~feet}{2}[/latex] • [latex]\frac{1~foot}{12~inches}[/latex] = ?
You could not cancel the feet because the unit is not the same in both the numerator and the denominator. So, if you complete the computation, you would still have both feet and inches in the answer and no conversion would take place.
| Example 2 | ||||||||||||||
| An interior decorator needs border trim for a home she is wallpapering. She needs 15 feet of border trim for the living room, 30 feet of border trim for the bedroom, and 26 feet of border trim for the dining room. How many yards of border trim does she need? | ||||||||||||||
The interior decorator needs [latex]23\frac{2}{3}[/latex] yards of border trim. |
| You Try MU.2.A |
| A. Use the Factor-Label Method to determine the number of feet in [latex]2\frac{1}{2}[/latex] miles.
B. A fence company is measuring a rectangular area in order to install a fence around its perimeter. If the length of the rectangular area is 130 yards and the width is 75 feet, what is the total length of the distance to be fenced? |
Weight/Mass
You often use the word weight to describe how heavy or light an object or person is. Weight is measured in the U.S. customary system using three units: ounces, pounds, and tons. An ounce is the smallest unit for measuring weight, a pound is a larger unit, and a ton is the largest unit. You can use any of the customary measurement units to describe the weight of something, but it makes more sense to use certain units for certain purposes. For example, it makes more sense to describe the weight of a human being in pounds rather than tons. It makes more sense to describe the weight of a car in tons rather than ounces.
The following table shows the unit conversions and conversion factors that are used to make conversions between customary units of weight.
| Unit Equivalents | Conversion Factors (heaver to lighter units of measurement) | Conversation Factors (light to heavier units of measurement) |
| 1 pound (lb) = 16 ounces (oz) | [latex]\frac{16~ounces}{1~pound}[/latex] | [latex]\frac{1~pound}{16~ounces}[/latex] |
| 1 ton (T) = 2,000 pounds (lb) | [latex]\frac{2,000~pounds}{1~ton}[/latex] | [latex]\frac{1~ton}{2,000~pounds}[/latex] |
| 1 tonne (t) = 1,000 kilograms (kg) | [latex]\frac{1,000~kilograms}{1~tonne}[/latex] | [latex]\frac{1~tonne}{1,000~kilograms}[/latex] |
| Example 3 | ||||||||||||
| Use the Factor Label Method to determine the number of ounces in [latex]2\frac{1}{4}[/latex] pounds. | ||||||||||||
There are 36 ounces in [latex]2\frac{1}{4}[/latex] pounds. |
There are times when you need to perform calculations on measurements that are given in different units. To solve these problems, you need to convert one of the measurements to the same unit of measurement as the other measurement. Think about whether the unit you are converting to is smaller or larger than the unit you are converting from. This will help you be sure that you are making the right computation. You can use the factor label method to make the conversion from one unit to another.
The following examples require converting between units of weight.
| Example 4 | ||||||||||||
| A municipal trash facility allows a person to throw away a maximum of 30 pounds of trash per week. Last week, 140 people threw away the maximum allowable trash. How many tons of trash did this equal? | ||||||||||||
The total amount of trash generated is: [latex]2\frac{1}{10}[/latex] tons |
| Example 5 | ||||||||||||||
| The post office charges $0.44 to mail something that weighs an ounce or less. The charge for each additional ounce, or fraction of an ounce, of weight is $0.17. At this rate, how much will it cost to mail a package that weighs 2 pounds 3 ounces? | ||||||||||||||
It will cost $6.22 to mail a package that weighs 2 pounds 3 ounces. |
| You Try MU.2.B |
| A. How many pounds is 72 ounces?
B. The average weight of a northern Bluefin tuna is 1,800 pounds. The average weight of a great white shark is [latex]2\frac{1}{2}[/latex] tons. On average, how much more does a great white shark weigh, in pounds, than a northern bluefin tuna? |
Capacity/Volume
Capacity is the amount of liquid (or other pourable substance) that an object can hold when it’s full. When a liquid, such as milk, is being described in gallons or quarts, this is a measure of capacity.
There are five main units for measuring capacity in the U.S. customary measurement system. The smallest unit of measurement is a fluid ounce. “Ounce” is also used as a measure of weight, so it is important to use the word “fluid” with ounce when you are talking about capacity. Sometimes the prefix “fluid” is not used when it is clear from the context that the measurement is capacity, not weight.
The other units of capacity in the customary system are the cup, pint, quart, and gallon. The table below describes each unit of capacity and provides an example to illustrate the size of the unit of measurement.
You can use any of these five measurement units to describe the capacity of an object, but it makes more sense to use certain units for certain purposes. For example, it makes more sense to describe the capacity of a swimming pool in gallons and the capacity of an expensive perfume in fluid ounces.
The table below shows some of the most common equivalents and conversion factors for the five customary units of measurement of capacity.
| Unit Equivalents | Conversion Factors (heavier to lighter units of measurement) | Conversion Factors (lighter to heavier units of measurement) |
| 1 tablespoon (Tbsp) = 3 teaspoons (tsp) | [latex]\frac{1~tablespoon}{3~teaspoons}[/latex] | [latex]\frac{3~teaspoons}{1~tablespoon}[/latex] |
| 1 fluid ounce (fl oz) = 2 tablespoons (Tbsp) | [latex]\frac{1~fluid~ounce}{2~tablespoons}[/latex] | [latex]\frac{2~tablespoons}{1~fluid~ounce}[/latex] |
| 1 cup (c) = 8 fluid ounces (fl oz) | [latex]\frac{1~cup}{8~fluid~ounces}[/latex] | [latex]\frac{8~fluid~ounces}{1~cup}[/latex] |
| 1 pint (pt) = 2 cups (c) | [latex]\frac{1~pint}{2~cups}[/latex] | [latex]\frac{2~cups}{1~pint}[/latex] |
| 1 quart (qt) = 2 pints (pt) | [latex]\frac{1~quart}{2~pints}[/latex] | [latex]\frac{2~pints}{1~quart}[/latex] |
| 1 gallon (gal) = 4 quarts (qt) | [latex]\frac{1~gallon}{4~quarts}[/latex] | [latex]\frac{4~quarts}{1~gallon}[/latex] |
As with converting units of length and weight, you can use the factor label method to convert from one unit of capacity to another.
| Example 6 | ||||||||||||
| Use the Factor Label Method to determine the number of pints in [latex]2\frac{3}{4}[/latex] gallons. | ||||||||||||
[latex]2\frac{3}{4}[/latex] gallons is the equivalent to 22 pints. |
| Example 7 | ||||||||||
| Natasha is making lemonade to bring to the beach. She has two containers. One holds one gallon and the other holds 2 quarts. If she fills both containers, how many cups of lemonade will she have? | ||||||||||
Natasha will have 24 cups lemonade. |
Another way to work the problem above would be to first change 1 gallon to 16 cups and change 2 quarts to 8 cups. Then add: 16 + 8 = 24 cups.
| You Try MU.2C |
| Alan is making chili. He is using a recipe that makes 24 cups of chili. He has a 5-quart pot and a 2-gallon pot and is trying to determine whether the chili will all fit in one of these pots. Which of the pots will fit the chili?
A. The chili will not fit into either of the pots. |
| Example 8 |
| a. Add the following: (You should answer in pounds and ounces, converting any ounces over 16 into pounds)
12 pounds 8 ounces + 8 pounds 11 ounces b. Subtract the following: (You should answer in feet and inches, converting any inches over 12 into feet) 12 feet 2 inches – 8 feet 7 inches |
| a. 12 pounds 8 ounces + 8 pounds 11 ounces
12 pounds + 8 pounds = 20 pounds 8 ounces + 11 ounces = 19 ounces 19 ounces – 16 ounces (1 pound) = 3 ounces 20 pounds + 1 pound = 21 pounds Answer: 21 pounds 3 ounces b. 12 feet 2 inches – 8 feet 7 inches 11 feet (2 inches + 12 inches = 14 inches) 14 inches – 7 inches = 7 inches 11 feet – 8 feet = 3 feet Answer: 3 feet 7 inches |
| Time Conversions |
| Unit Equivalents | Conversion Factors (heavier to lighter units of measurement) | Conversion Factors (lighter to heavier units of measurement) |
| 1 minute (min) = 60 seconds (sec) | [latex]\frac{1~minute}{60~seconds}[/latex] | [latex]\frac{60~seconds}{1~minute}[/latex] |
| 1 hour (hr) = 60 minutes (min) | [latex]\frac{1~hour}{60~minutes}[/latex] | [latex]\frac{60~minutes}{1~hour}[/latex] |
| 1 day = 24 hours (hr) | [latex]\frac{1~day}{24~hours}[/latex] | [latex]\frac{24~hours}{1~day}[/latex] |
| 1 week = 7 days | [latex]\frac{1~week}{7~days}[/latex] | [latex]\frac{7~days}{1~week}[/latex] |
| 1 year = 52 weeks | [latex]\frac{1~year}{52~weeks}[/latex] | [latex]\frac{52~weeks}{1~year}[/latex] |
| 1 year = 365 days (except leap year) | [latex]\frac{1~year}{365~days}[/latex] | [latex]\frac{365~days}{1~year}[/latex] |
| Example 9 | |||
| a. Convert 480 minutes into seconds.
b. Convert 949 weeks into years. c. Convert 714 minutes into hours and minutes. |
|||
|
| Example 10 |
| a. Add: 11 hours 38 minutes plus 7 hours 45 minutes
(You should answer in hours and minutes, converting any minutes over 59 into hours) b. Subtract: 11 hours 38 minutes minus 7 hours 45 minutes (You should answer in hours and minutes, converting any minutes over 59 into hours) |
| a. Add: 11 hours 38 minutes plus 7 hours 45 minutes
11 hours 38 minutes + 7 hours 45 minutes ———————– 18 hours 83 minutes (Converting any minutes over 59 into hours)
83 minutes (60 minutes plus 23 minutes) 83 minutes (1 hour plus 23 minutes) Add 1 hour to 18 hours Answer: 19 hours 23 minutes
b. Subtract: 11 hours 38 minutes minus 7 hours 45 minutes 10 hours (38 minutes + 60 minutes = 98 minutes) 10 hours 98 minutes – 7 hours 45 minutes ———————– 3 hours 53 minutes Answer: 3 hours 53 minutes |
| Square and Cubic Unit Conversions |
We learned that 1 foot = 12 inches, consider the following diagram:
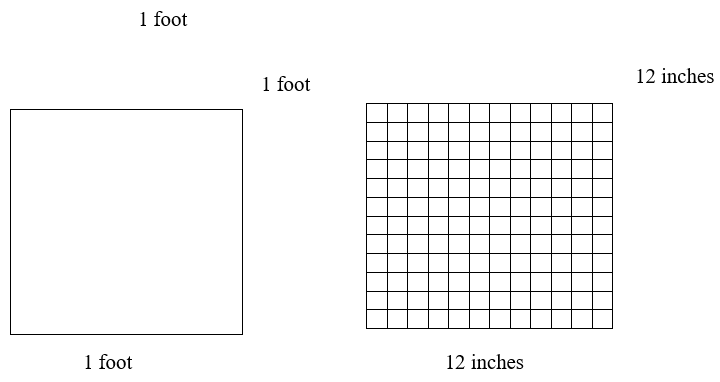
Similarly, we learned that 1 yard = 3 feet, consider the following diagram:
Therefore, 1 ft2 = 144 in2
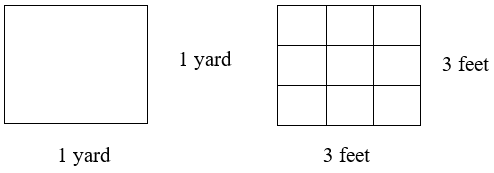
Therefore, 1 yd2 = 9 ft2
| Example 11 |
| The area of a basketball court is 4508 square feet. What is the area of the basketball court in square inches? |
| We know 1 foot = 12 inches.
[latex]\frac{4,508~ft^\bcancel{2}}{1}[/latex] • [latex]\frac{12~in}{1~\bcancel{ft}}[/latex] • [latex]\frac{12~in}{1~\bcancel{ft}}[/latex] = 4,508 • in • in = 649,152 in2 The area of the basketball court is 649,152 in2. |
| Example 12 |
| A swimming pool has a volume of 17,163 cubic feet. How many cubic yards is the swimming pool? Round to the nearest tenth. |
| We know 1 yard = 3 feet.
[latex]\frac{17,163~ft^\bcancel{3}}{1}[/latex] • [latex]\frac{1~yd~\cdot~1~yd~\cdot~1~yd}{3~\bcancel{ft}~\cdot~3~\bcancel{ft}~\cdot~3~\bcancel{ft}}[/latex] = [latex]\frac{17,163~\cdot~yd~\cdot~yd~\cdot~yd}{3~\cdot~3~\cdot~3}[/latex] = [latex]\frac{17,163~yd^3}{27}[/latex] 635.7 yd3 The swimming pool is 635.7 yd3. |
| You Try MU.2.D |
| Perform the following conversions.
a. Convert 54 square feet to square inches b. Convert 54 cubic inches to cubic feet |
Section MU.2 – Answers to You Try Problems
MU.2.A
A. 13,200 feet
B. 930 feet or 310 yards
MU.2.B
A. 4.5 pounds
B. 3,200 pounds
MU.2.C
D. The chili will fit into the 2-gallon pot only.
MU.2.D
A. 7776 in2
B. 0.03125 ft3

