Section PC.3 – Expected Value Practice Problems
1. Determine whether each statement is true or false.
a. If the Expected Value of a game is zero, we say that it is a 'fair game'.
b. The probability of an event that is certain is 0.
c. Expected Value is the actual gain or loss each time an event takes place.
d. If P(A) is the probability that event A will occur, the probability event A will not occur is P(Ā) = 1 - P(A).
e. Expected Value is the average gain or loss of an event if the procedure is repeated many times.
f. The probability of an impossible event is −1.
g. If the odds for an event are 3 to 5, then the odds against that event are 5 to 3.
2. Determine whether each statement is true or false.
a. If P(A) is the probability that event A will occur, the probability event A will not occur is P(Ā) = -P(A).
b. Expected Value is the average gain or loss of an event if the procedure is repeated many times.
c. The probability of an event that is certain is 1.
d. If the Expected Value of a game is 1, we say that it is a 'fair game'.
e. Expected Value is the actual gain or loss each time an event takes place.
f. If the odds for an event are 3 to 5, then the odds against that event are 5 to 3.
g. The probability of an impossible event is 0.
3. A bag contains 3 gold marbles, 6 silver marbles, and 28 black marbles. Someone offers to play this game: You randomly select on marble from the bag. If it is gold, you win $3. If it is silver, you win $2. If it is black, you lose $1. What is your expected value if you play this game?
4. A bag contains 2 gold marbles, 10 silver marbles, and 25 black marbles. Someone offers to play this game: You randomly select one marble from the bag. If it is gold, you win $3. If it is silver, you win $2. If it is black, you lose $1. What is your expected value if you play this game?
5. A friend devises a game that is played by rolling a single six-sided die once. If you roll a 6, he pays you $3; if you roll a 5, he pays you nothing; if you roll a number less than 5, you pay him $1. Compute the expected value for this game. Should you play this game?
6. A company estimates that 0.7% of their products will fail after the original warranty period but within 2 years of the purchase, with a replacement cost of $350. If they offer a 2 year extended warranty for $48, what is the company's expected value of each warranty sold?
7. A company estimates that 0.9% of their products will fail after the original warranty period but within 2 years of the purchase, with a replacement cost of $500. If they offer a 2 year extended warranty for $45, what is the company's expected value of each warranty sold?
8. An insurance company estimates the probability of an earthquake in the next year to be 0.0013. The average damage done by an earthquake it estimates to be $60,000. If the company offers earthquake insurance for $100, what is their expected value of the policy?
9. A game is played using one die. If the die is rolled and shows 1, the player wins $1; if 2, the player wins $2; if 3, the player wins $3. If the die shows 4, 5, or 6, the player wins nothing. If there is a charge of $1.25 to play the game, what is the game’s expected value?
10. The PTO is selling raffle tickets to raise money for classroom supplies. A raffle ticket costs $2. There is 1 winning ticket out of the 290 tickets sold. The winner gets a prize worth $98. Round your answers to the nearest cent.
a. What is the expected value (to you) of one raffle ticket?
b. Calculate the expected value (to you) if you purchase 6 raffle tickets.
c. What is the expected value (to the PTO) of one raffle ticket?
d. If the PTO sells all 290 raffle tickets, how much money can they expect to raise for the classroom supplies?
11. One of the games at a carnival is Spin the Pointer, which uses a spinner like the one picture below. A carnival ticket that cost $2.00 is required to play the game. For each $2.00 ticket, a player spins the pointer once and receives the amount of money indicated in the sector where the pointer lands on the wheel. The spinner has an equal probability of landing in each of the 8 sectors.
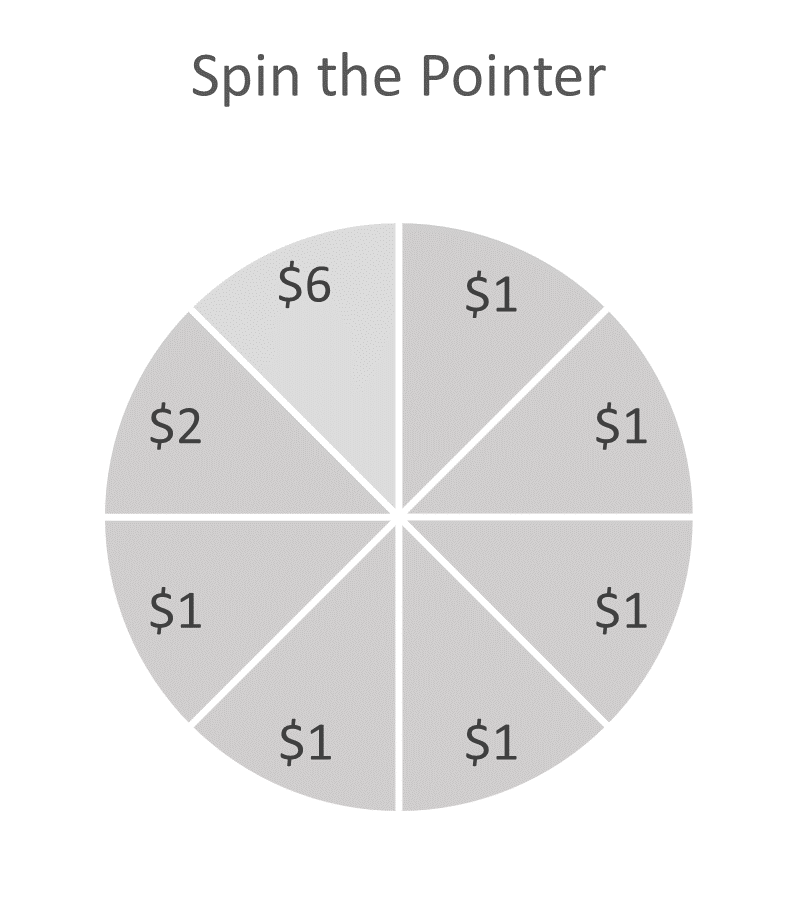
12. You are raising money for a local charity and plan on spending $1500 in upfront costs to host a tennis tournament. You expect to sell tickets worth $7000 the day of the tournament. However, if it rains on the day of the forecast tournament, you won’t sell any tickets and will lose all the money spent in upfront costs. If the weather for the tournament day is 35% chance of rain, what is your expected return? Is it a good idea to spend the money on upfront costs?
13. The table below give recent prizes and probabilities of winning (on a single $1 ticket) for a certain lottery. Find the expected value of the winnings for a single lottery ticket, given the following values. Is it a good idea to play this lottery?
| Prize | Probability |
| Win free ticket (worth $1) | [latex]\frac{1}{5}[/latex] |
| Win $5 | [latex]\frac{1}{100}[/latex] |
| Win $1000 | [latex]\frac{1}{100,000}[/latex] |
| Win $1,000,000 | [latex]\frac{1}{10,000,000}[/latex] |
14. A game is played using a standard 52-card deck. The player pays $3 to play and gets to pick one card at random from the deck. If the player picks an ace, they win $16. If they pick a face card, they win $8. If the player picks a numbered card, they win $3. What is the expected value of the game?
15. In a game of one-spot Keno, a card is purchased for $2. It allows a player to choose one number from 1 to 80. The dealer then chooses twenty numbers at random from 1 to 80. If the player's number is among the numbers chosen by the dealer then the player is paid $3.90, but does not get to keep the $2 paid to play the game. Find the expected value of buying one card.
16. (Multiple Choice)
You are betting on a game in which each bet has an expected value of -$0.34. This means that:
a. You will win 34 cents every time you play.
b. You will lose 34 cents every time you play.
c. If you play the game many times, on average you will have won about 34 cents per game.
d. If you play the game many times, on average you will have lost about 34 cents per game.

