Section PC.4 Practice Problems
1. Lacy draws a ‘3’ from a standard deck of 52 cards. Without replacing the first card, she then proceeds to draw a second card and gets a ’10’. Are these events independent or dependent?
2. Linda draws a ‘3’ from a standard deck of 52 cards. She replaces the first card and proceeds to draw a second card and gets a ’10’. Are these events independent or dependent?
3. A 6-sided die rolled twice. Let E be the event “the first roll is a 6” and F the event “the second roll is a 6”.
a. Are the events E and F independent or dependent?
b. Find the probability of showing a 6 on both rolls.
4. A six-sided die is rolled twice. What is the probability of showing a 2 on the first roll and an odd number on the second roll?
5. A six-sided die is rolled three times. What is the probability of showing an even number on all three rolls?
6. A six-sided die is rolled twice. What is the probability of showing a 6 on both rolls?
7. A fair coin is flipped twice. What is the probability of showing heads on both flips?
8. A die is rolled twice. What is the probability of showing a 5 on the first roll and an even number on the second roll?
9. A couple has three children. What is the probability that all three are girls?
10. Suppose that 21% of people own dogs. If you pick two people at random, what is the probability that they both own a dog?
11. In your drawer you have 5 pairs of socks, 4 of which are white, and 11 tee shirts, 2 of which are white. If you randomly reach in and pull out a pair of socks and a tee shirt, what is the probability that both are white?
12. Sara draws the 3 of hearts from a standard deck of 52 cards. Without replacing the first card, she then proceeds to draw a second card. Write answer as simplified fraction.
a. Determine the probability that the second card is another 3. P(3 | 3 of hearts) =
b. Determine the probability that the second card is another heart. (heart | 3 of hearts) =
c. Determine the probability that the second card is a club. P(club | 3 of hearts) =
d. Determine the probability that the second card is a 9. P(9 | 3 of hearts) =
13. Bert and Ernie each have a well-shuffled standard deck of 52 cards. They each draw one card from their own deck. Compute the probability that:
a. Bert and Ernie both draw an Ace.
b. Bert draws an Ace but Ernie does not.
c. Neither Bert nor Ernie draws an Ace.
d. Bert and Ernie both draw a heart.
e. Bert gets a card that is not a Jack and Ernie draws a card that is not a heart.
14. Bert has a well-shuffled standard deck of 52 cards, from which he draws one card; Ernie has a 12-sided die, which he rolls at the same time Bert draws a card. Compute the probability that:
a. Bert gets a Jack and Ernie rolls a five.
b. Bert gets a heart and Ernie rolls a number less than six.
c. Bert gets a face card (Jack, Queen or King) and Ernie rolls an even number.
d. Bert gets a red card and Ernie rolls a fifteen.
e. Bert gets a card that is not a Jack and Ernie rolls a number that is not twelve.
15. A jar contains 5 red marbles numbered 1 to 5 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is:
a. Even-numbered given that the marble is red.
b. Red given that the marble is even-numbered.
16. A jar contains 4 red marbles numbered 1 to 4 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is:
a. Odd-numbered given that the marble is blue.
b. Blue given that the marble is odd-numbered.
17. A survey was conducted at a local ballroom dance studio asking students if they had ever competed in the following dance categories:
-Smooth
-Rhythm
-Standard
The results were then presented to the owner in the following Venn Diagram:
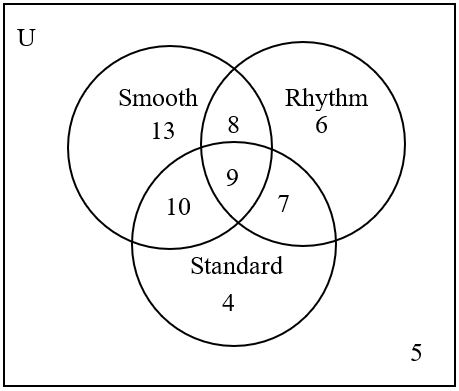
Use the Venn Diagram to determine the following probabilities. Write your answers in percent form, rounded to the nearest tenth.
a. If a student is chosen at random, what is the probability that the student competed in Rhythm GIVEN they had competed in Smooth. P(Rhythm∣∣Smooth) =
b. If a student is chosen at random, what is the probability that the student competed in Rhythm GIVEN they had competed in Standard. P(Rhythm∣∣Standard) =
c. If a student is chosen at random, what is the probability that the student competed in Standard GIVEN they had competed in Rhythm. P(Standard∣∣Rhythm) =
d. If a student is chosen at random, what is the probability that the student competed in Rhythm GIVEN they had competed in Smooth or Standard. P(Rhythm∣∣Smooth or Standard) =
18. Compute the probability of flipping a coin and getting heads, given that the previous flip was tails.
19. Find the probability of rolling a “1” on a fair die, given that the last 3 rolls were all ones.
20. Suppose a math class contains 25 students, 14 females (three of whom speak French) and 11 males (two of whom speak French).
a. Compute the probability that a randomly selected student speaks French, given that the student is female.
b. Compute the probability that a randomly selected student is male, given that the student speaks French.
21. A test was given to a group of students. The grades and gender are summarized below.
| A | B | C | Total | |
| Male | 10 | 12 | 2 | 24 |
| Female | 16 | 6 | 9 | 31 |
| Total | 26 | 18 | 11 | 55 |
Suppose a student is chosen at random:
a. Find the probability that the student was male given they earned an A.
b. Find the probability that the student was male given they earned a C.
c. Find the probability that the student was female given they earned a B.
22. A test was given to a group of students. The grades and gender are summarized below.
| A | B | C | Total | |
| Male | 7 | 6 | 4 | 17 |
| Female | 9 | 2 | 10 | 21 |
| Total | 16 | 8 | 14 | 38 |
Suppose a student is chosen at random:
a. Find the probability that the student earned a B given they are male.
b. Find the probability that the student earned a B given they are female.
c. Find the probability that the student earned a C given they are male.
23. A certain virus infects 100 in every 40,000 people. A test used to detect the virus in a person is positive 90% of the time if the person has the virus and 10% of the time if the person does not have the virus. Let A be the event “the person is infected” and B be the event “the person tests positive”. Round your answers 4 decimal places.
a. Find the probability that a person has the virus given that they have tested positive, i.e. find P(A | B).
b. Find the probability that a person does not have the virus given that they test negative, i.e. find P(not A | not B).
24. A certain virus infects one in every 2000 people. A test used to detect the virus in a person is positive 96% of the time if the person has the virus and 4% of the time if the person does not have the virus. Let A be the event “the person is infected” and B be the event “the person tests positive”. Round your answers to 5 decimals places.
a. Find the probability that a person has the virus given that they have tested positive, i.e. find P(A | B).
b. Find the probability that a person does not have the virus given that they test negative, i.e. find P(not A | not B).
25. Two cards are drawn from a standard deck of cards. What is the probability of drawing a King and then drawing a Queen?
26. Two cards are drawn from a standard deck of cards. What is the probability of both cards being red?
27. Two cards are drawn from a standard deck of cards. What is the probability of drawing a Jack and then drawing an Ace?
28. Five cards are drawn from a standard deck of cards. What is the probability of all cards being black?
29. Tony buys a bag of cookies that contains 4 chocolate chip cookies, 9 peanut butter cookies, 7 sugar cookies and 8 oatmeal cookies. What is the probability that Tony reaches in the bag and randomly selects a peanut butter cookie from the bag, eats it, then reaches back in the bag and randomly selects a sugar cookie?
30. Suppose a jar contains 17 red marbles and 32 blue marbles. If you reach in the jar and pull out 2 marbles at random, find the probability that both are red.
31. Suppose you write each letter of the alphabet on a different slip of paper and put the slips into a hat. If you pull out two slips at random, find the probability that both are vowels.
32. A math class consists of 25 students, 14 female and 11 male. Two students are selected at random to participate in a probability experiment. Compute the probability that:
a. a male is selected, then a female.
b. a female is selected, then a male.
c. two males are selected.
d. two females are selected.
e. no males are selected.
33. A math class consists of 25 students, 14 female and 11 male. Three students are selected at random to participate in a probability experiment. Compute the probability that:
a. a male is selected, then two females.
b. a female is selected, then two males.
c. two females are selected, then one male.
d. three males are selected.
e. three females are selected.

