Section PC.5 Practice Problems
Write answers as whole numbers or simplified fractions unless otherwise noted.
1. A test was given to a group of students. The grades and gender are summarized below.
| A | B | C | Total | |
| Male | 8 | 18 | 13 | 39 |
| Female | 10 | 4 | 12 | 26 |
| Total | 18 | 22 | 25 | 65 |
Suppose a student is chosen at random:
a. Find the probability that the student is female and earned an A.
b. Find the probability that the student is male and earned an A.
c. Find the probability that the student is male or earned a C.
d. Find the probability that the student is female or earned a B
2. The table below shows the number of credit cards owned by a group of individuals.
| Zero Cards | One Card | Two+ Cards | Total | |
| Male | 9 | 5 | 19 | 33 |
| Female | 18 | 10 | 20 | 48 |
| Total | 27 | 15 | 39 | 81 |
Suppose a person is chosen at random:
a. Find the probability that the person is male and has two+ credit cards.
b. Find the probability that the person is female and has one credit card.
c. Find the probability that the person is male or has no credit cards.
d. Find the probability that the person is female or has no credit cards.
3. Suppose we draw one card from a standard deck. What is the probability of drawing the King of hearts or a Queen?
4. Suppose you roll a six-sided die. What is the probability that you roll an even number or a five?
5. Suppose we draw one card from a standard deck. What is the probability of drawing a King or a heart?
6. Suppose we draw one card from a standard deck. What is the probability of drawing a face card or a diamond?
7. Suppose we draw one card from a standard deck. What is the probability of drawing a Jack or a black card?
8. Two six-sided dice are rolled. What is the probability of getting a sum of either 11 or 12?
9. A jar contains 6 red marbles numbered 1 to 6 and 8 blue marbles numbered 1 to 8. A marble is drawn at random from the jar. Find the probability the marble is red or odd-numbered.
10. A jar contains 4 red marbles numbered 1 to 4 and 10 blue marbles numbered 1 to 10. A marble is drawn at random from the jar. Find the probability the marble is blue or even-numbered.
11. A jar contains 4 red marbles numbered 1 to 4 and 12 blue marbles numbered 1 to 12. A marble is drawn at random from the jar. Find the probability of the given event.
a. The marble is red or odd-numbered
b. The marble is blue and even-numbered
12. Given the following information, determine P(A or B).
P(A) = 0.56
P(B) = 0.53
P(A and B) = 0.42
P(B|A) = 0.3
13. Given the following information, determine P(A or B).
P(A) = 0.76
P(B) = 0.3
P(A and B) = 0.28
P(B|A) = 0.2
14. A glass jar contains 1 red, 3 green, 2 blue, and 4 yellow marbles. If a single marble is chosen at random from the jar, what is the probability that it is yellow or green?
15. A day of the week is chosen at random. What is the probability of choosing a Monday or Tuesday?
16. 22 customers are eating dinner at an Italian restaurant. Of the 22 customers, 18 order pizza, 10 order a salad, and 8 order pizza and salad. Using this information, answer each of the following questions. Let A be the event that a randomly selected customer orders pizza and B be the event that a randomly selected customer orders a salad.
a. What is P(A), the probability that a customer orders pizza?
b. What is P(B), the probability that a customer orders salad?
c. What is P(A and B), the probability that a customer orders pizza and salad?
d. What is P(A or B), the probability that a customer orders pizza or a salad?
17. On New Year’s Eve, the probability of a person having a car accident is 0.15. The probability of a person driving while intoxicated is 0.32. The probability of a person having a car accident and driving while intoxicated is 0.09. What is the probability of a person driving while intoxicated or having a car accident?
18. In a statistics class there are 18 juniors and 10 seniors; 6 of the seniors are females and 12 of the juniors are males. If a student is selected at random, find the probability of selecting the following:
a. P(a junior or a female)
b. P(a junior or a senior)
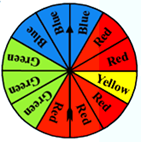
19. It is equally probable that the pointer on the spinner shown will land on any one of the regions. If the pointer land on a borderline, spin again. Find the probability that the pointer will stop on a red or blue region.
20. A recent study of 200 nurses found that of 125 female nurses, 56 had bachelor’s degrees; and of 75 male nurses, 34 had bachelor’s degrees. If a nurse is selected at random, find the probability that the nurse is:
a. a female nurse with a bachelor’s degree
b. a male nurse
c. a male nurse with a bachelor’s degree
d. based on your answer to a, b, and c, explain which is most likely to occur. Why?
21. Below is a list of all possible outcomes in the experiment of rolling two die.
| 1 , 1 | 1 , 2 | 1 , 3 | 1 , 4 | 1 , 5 | 1 , 6 |
| 2 , 1 | 2 , 2 | 2 , 3 | 2 , 4 | 2 , 5 | 2 , 6 |
| 3 , 1 | 3 , 2 | 3 , 3 | 3 , 4 | 3 , 5 | 3 , 6 |
| 4 , 1 | 4 , 2 | 4 , 3 | 4 , 4 | 4 , 5 | 4 , 6 |
| 5 , 1 | 5 , 2 | 5 , 3 | 5 , 4 | 5 , 5 | 5 , 6 |
| 6 , 1 | 6 , 2 | 6 , 3 | 6 , 4 | 6 , 5 | 6 , 6 |
Determine the following probabilities. Write answer as simplified fraction.
a. P( sum is odd)
b. P( sum is odd)
c. P( sum is 7)
d. P( sum is 7 and at least one of the die is a 1)
e. P( sum is 7 or at least one of the die is a 1)
22. A survey was conducted at a local ballroom dance studio asking 86 students if they had ever competed in the following dance categories: Smooth, Rhythm, or Standard. The results were then presented to the owner in the following Venn Diagram.
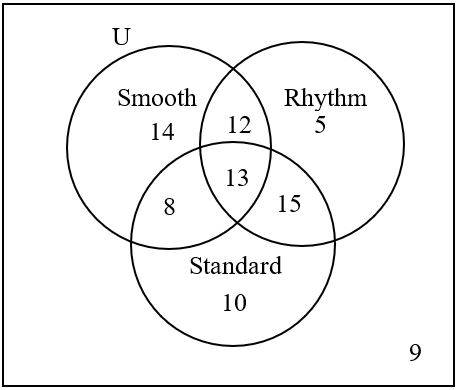
Determine the following probabilities. Write your answers in percent form, rounded to the nearest tenth.
a. P(Smooth)
b. P(Rhythm and Standard)
c. P(Smooth or Standard)
d. P(not Smooth)

