Section PC.6 – Basic Counting and Permutations
Basic Counting
Counting? You already know how to count or you wouldn't be taking a college-level math class, right? Well yes, but what we'll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don't want to do this.
We will start, however, with some more reasonable sorts of counting problems in order to develop the ideas that we will soon need.
| Example 1 | |||||||||||||||||||||||||||||||||||
| Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pizza). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have? | |||||||||||||||||||||||||||||||||||
Solution 1: One way to solve this problem would be to systematically list each possible meal:
If we did this systematically, and neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus, you could go to the restaurant 15 nights in a row and have a different meal each night. Solution 2: Another way to solve this problem would be to list all the possibilities in a table:
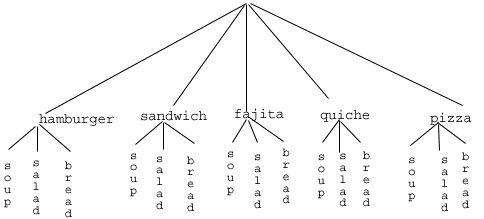
In each of the cells in the table we could list the corresponding meal: soup + hamburger in the upper left corner, salad + hamburger below it, etc. But if we didn't really care what the possible meals are, only how many possible meals there are, we could just count the number of cells and arrive at an answer of 15, which matches our answer from the first solution. (It's always good when you solve a problem two different ways and get the same answer!) Solution 3: We already have two perfectly good solutions. Why do we need a third? The first method was not very systematic, and we might easily have made an omission. The second method was better, but suppose that in addition to the appetizer and the main course we further complicated the problem by adding desserts to the menu: we've used the rows of the table for the appetizers and the columns for the main courses—where will the desserts go? We would need a third dimension, and since drawing 3-D tables on a 2-D page or computer screen isn't terribly easy, we need a better way in case we have three categories to choose from instead of just two. So, back to the problem in the example. What else can we do? Let's draw a tree diagram:
This is called a "tree" diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15. If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches. |
OK, so now we know how to count possibilities using tables and tree diagrams. These methods will continue to be useful in certain cases, but imagine a game where you have two decks of cards (with 52 cards in each deck) and you select one card from each deck. Would you really want to draw a table or tree diagram to determine the number of outcomes of this game?
Let's go back to the previous example that involved selecting a meal from three appetizers and five main courses, and look at the second solution that used a table. Notice that one way to count the number of possible meals is simply to number each of the appropriate cells in the table, as we have done above. But another way to count the number of cells in the table would be multiply the number of rows (3) by the number of columns (5) to get 15. Notice that we could have arrived at the same result without making a table at all by simply multiplying the number of choices for the appetizer (3) by the number of choices for the main course (5). We generalize this technique as the basic counting rule:
| Basic Counting Rule |
|
If we are asked to choose one item from each of two separate categories where there are m items in the first category and n items in the second category, then the total number of available choices is m · n. This is sometimes called the multiplication rule for probabilities. |
| Example 2 |
| There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter? |
| There are 21 choices from the first category and 18 for the second, so there are 21 · 18 = 378 possibilities. |
The Basic Counting Rule can be extended when there are more than two categories by applying it repeatedly, as we see in the next example.
| Example 3 |
| Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have? |
| There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are 3 · 5 · 2 = 30 possibilities. |
| You Try PC.6.A |
| You are making your schedule for next semester. You have 5 choices for your math class, 8 choices for your English class, 3 choices for your communications class, and 4 choices for your elective. How many different schedules are possible? |
| Example 4 |
| A quiz consists of 3 true-or-false questions. In how many ways can a student answer the quiz? |
| There are 3 questions. Each question has 2 possible answers (true or false), so the quiz may be answered in 2 · 2 · 2 = 8 different ways. Recall that another way to write 2 · 2 · 2 is 23, which is much more compact. |
Permutations
We will now develop an even faster way to solve some of the problems we have already learned to solve by other means. Let's start with a couple examples.
| Example 5 |
| How many different ways can the letters of the word MATH be rearranged to form a four-letter code word? |
| This problem is a bit different. Instead of choosing one item from each of several different categories, we are repeatedly choosing items from the same category (the category is: the letters of the word MATH) and each time we choose an item we do not replace it, so there is one fewer choice at the next stage: we have 4 choices for the first letter (say we choose A), then 3 choices for the second (M, T and H; say we choose H), then 2 choices for the next letter (M and T; say we choose M) and only one choice at the last stage (T). Thus there are 4 · 3 · 2 · 1 = 24 ways to spell a code worth with the letters MATH. |
| Factorial |
|
n ! = n · (n – 1) · (n – 2) ··· 3 · 2 · 1 |
| Example 6 |
| How many ways can five different door prizes be distributed among five people? |
| There are 5 choices of prize for the first person, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be 5! = 5 · 4 · 3 · 2 · 1 = 120 ways. |
| You Try PC.6.B |
| A little league baseball team has 12 players. How many different batting orders of the 12 players are possible? |
| Example 7 |
| A charity benefit is attended by 25 people and three gift certificates are given away as door prizes: one gift certificate is in the amount of $100, the second is worth $25 and the third is worth $10. Assuming that no person receives more than one prize, how many different ways can the three gift certificates be awarded? |
| Using the Basic Counting Rule, there are 25 choices for the person who receives the $100 certificate, 24 remaining choices for the $25 certificate and 23 choices for the $10 certificate, so there are 25 · 24 · 23 = 13,800 ways in which the prizes can be awarded. |
| Example 8 |
| Eight sprinters have made it to the Olympic finals in the 100-meter race. In how many different ways can the gold, silver and bronze medals be awarded? |
| Using the Basic Counting Rule, there are 8 choices for the gold medal winner, 7 remaining choices for the silver, and 6 for the bronze, so there are 8 · 7 · 6 = 336 ways the three medals can be awarded to the 8 runners. |
Note that in these preceding examples, the gift certificates and the Olympic medals were awarded without replacement; that is, once we have chosen a winner of the first door prize or the gold medal, they are not eligible for the other prizes. Thus, at each succeeding stage of the solution there is one fewer choice (25, then 24, then 23 in the first example; 8, then 7, then 6 in the second). Contrast this with the situation of a multiple choice test, where there might be five possible answers — A, B, C, D or E — for each question on the test.
Note also that the order of selection was important in each example: for the three door prizes, being chosen first means that you receive substantially more money; in the Olympics example, coming in first means that you get the gold medal instead of the silver or bronze. In each case, if we had chosen the same three people in a different order there might have been a different person who received the $100 prize, or a different gold medalist. (Contrast this with the situation where we might draw three names out of a hat to each receive a $10 gift certificate; in this case the order of selection is not important since each of the three people receive the same prize. Situations where the order is not important will be discussed in the next section.)
We can generalize the situation in the two examples above to any problem without replacement where the order of selection is important. If we are arranging in order r items out of n possibilities (instead of 3 out of 25 or 3 out of 8 as in the previous examples), the number of possible arrangements will be given by
n · (n – 1) · (n – 2) ··· (n – r + 1)
If you don't see why (n — r + 1) is the right number to use for the last factor, just think back to the first example in this section, where we calculated 25 · 24 · 23 to get 13,800. In this case n = 25 and r = 3, so n — r + 1 = 25 — 3 + 1 = 23, which is exactly the right number for the final factor.
Now, why would we want to use this complicated formula when it's actually easier to use the Basic Counting Rule, as we did in the first two examples? Well, we won't actually use this formula all that often, we only developed it so that we could attach a special notation and a special definition to this situation where we are choosing r items out of n possibilities without replacement and where the order of selection is important. In this situation we write:
| Permutations |
|
nPr = n · (n – 1) · (n – 2) ··· (n – r + 1) We say that there are nPr permutations of size r that may be selected from among n choices without replacement when order matters. It turns out that we can express this result more simply using factorials. nPr = [latex]\frac{n!}{(n~-~r)!}[/latex] |
In practicality, we usually use technology rather than factorials or repeated multiplication to compute permutations.
| Example 9 |
| I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this? |
| Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are 9P4 = 9 · 8 · 7 · 6 = 3,024 permutations
To enter 9P4 in your graphing calculator, type 9, then hit the MATH key, scroll over to PRB, select option “2:nPr” by hitting enter. Your main screen should now show “9 nPr” and have a blinking cursor. Type 4, so that your calculator shows “9 nPr 4”. Hit enter and you will get the answer 3,024. |
| Example 10 |
| How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization? |
| We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is 16P4 = 16 · 15 · 14 · 13 = 43,680. |
| You Try PC.6.C |
| How many 5 character passwords can be made using the letters A through Z
a. if repeats are allowed b. if no repeats are allowed |
| Permutations of Duplicate Items |
|
The number of permutations of n items, where p items are identical, q items are identical, r items are identical, and so on, is given by [latex]\frac{n!}{p!~q!~r!~...}[/latex] |
| Example 11 |
| a) How many distinct permutations can be formed using the letters of the word TENNESSEE?
b) In how many ways can the digits in the number 2,826,886 be arranged? |
| a) TENNESSEE has 9 letters. The letter E repeats four times, the letter N repeats two times, the letter S repeats two times.
[latex]\frac{9!}{4!~2!~2!}[/latex] = 3780 b) 2,826,883 has 7 digits. The number 2 repeats two times, the number 8 repeats three times. [latex]\frac{7!}{2!~3!}[/latex] = 420 |
Section PC.6 Answers to You Try Problems
PC.6.A
480 different schedules are possible
PC.6.B
479,001,600
PC.6.C
a. 265 = 11,881,376
b. 26P5 = 7,893,600