Section PF.12 – Loans
In the last section, you learned about payout annuities.
In this section, you will learn about conventional loans (also called amortized loans or installment loans). Examples include auto loans and home mortgages. These techniques do not apply to payday loans, add-on loans, or other loan types where the interest is calculated up front.
One great thing about loans is that they use exactly the same formula as a payout annuity. To see why, imagine that you had $10,000.00 invested at a bank, and started taking out payments while earning interest as part of a payout annuity, and after 5 years your balance was zero. Flip that around, and imagine that you are acting as the bank, and a car lender is acting as you. The car lender invests $10,000.00 in you. Since you’re acting as the bank, you pay interest. The car lender takes payments until the balance is zero.
Suppose you borrow $1,000.00 at a 12% annual interest rate. Again, we assume that the account is compounded with the same frequency as we make payments unless stated otherwise.
In this example with monthly payments, we assume the 12% is compounded monthly (or 1% each month). So, you make your first $100.00 payment at the end of the first month. At the end of the second month, you make another $100.00 payment, but you also have to add 1% interest on the prior balance (in this case 1% of $1,000.00 = $10.00) making the new balance (amount owed) $910.00 at the end of month 2.
In general,
Ending Balance = Prior Balance + 1% Interest on Prior Balance – Monthly Payment
The table below shows this process over 3 months. This table is called an amortization table.
| Month | Prior Balance | 1% Interest on Prior Balance | Monthly Payment | Ending Balance |
| 0 |
|
|
|
$1,000.00 |
| 1 | $1,000.00 | $10.00 | $100.00 | $910.00 |
| 2 | $910.00 | $9.10 | $100.00 | $819.10 |
| 3 | $819.10 | $8.19 | $100.00 | $727.29 |
| And so on |
… |
… |
… |
… |
Notice that each month, the interest that must be paid decreases slightly (because you have made a payment that has decreased the principal). In an installment loan, the monthly payments are a fixed amount, so early on in the loan a larger proportion of your payment is being applied to interest, and a smaller proportion of your payment is being applied toward paying down the principal. As the term of the loan proceeds, the proportion of the payment going toward interest gradually decreases, and the proportion of the payment going toward principal gradually increases.
As an example, the graph below shows the relationship between the amount of the payment going towards principal, and the amount of the payment going towards interest for a 30-year mortgage.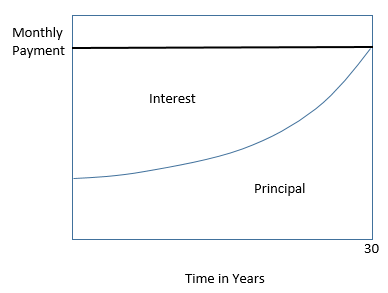
| Example 1 |
| You take out a 5 year installment loan to purchase a new vehicle. Your monthly payment is fixed at $485.22 for those 5 years, after which you will have paid off the loan in full. Will a larger proportion of your payment go towards principal during year 1 of the loan, or year 4 of the loan? |
|
You owe the most money on your car when you first buy it. Since the interest due is calculated based on how much you currently owe on the loan, you owe the most interest during the first month. Keep in mind that your payment is a fixed amount, $485.22. Early in the loan, a larger proportion of your payment is going towards paying interest, while a smaller proportion of your payment is being applied to principal. As you gradually decrease your principal (the amount you owe), your interest due each month decreases as well. This means that over the life of the loan, a larger proportion of your payment can be used to pay down the principal. During year 4 of the loan, a larger proportion of the fixed payment will go towards principal than during year 1 of the loan. |
The following formula generalizes the installment loan process:
| Loan Formula |
|
P0 = [latex]\large{\frac{PMT(1~-~(1~+~\frac{r}{n})^{(-nt)})}{(\frac{r}{n})}}[/latex] P0 is the balance in the account at the beginning (starting amount, or principal). PMT is your loan payment (your monthly payment, annual payment, etc.) r is the annual interest rate (APR) in decimal form (Example 5% = 0.05) n is the number of compounding periods in one year. t is the number of years we plan to borrow the money (length of the loan, in years) |
Like before, the compounding frequency is not always explicitly given, but is determined by how often you make payments.
| When do you use the Loan Formula? |
|
The loan formula assumes that you make loan payments on a regular schedule (every month, year, quarter, etc.) and are paying interest on the loan. Compound interest: One deposit Annuity: Many deposits. Payout Annuity: Many withdrawals Loans: Many payments |
| Example 2 |
| Abigale can afford $200.00 per month as a car payment. If she can get an auto loan at 3% interest for 60 months (5 years), how expensive of a car can she afford (in other words, what amount loan can Abigale pay off with $200 per month)? |
|
In this example, we are looking for P0, the starting amount of the loan. Putting this into the equation: P0 = [latex]\frac{200(1~-~(1~+~\frac{0.03}{12})^{(-5~\cdot~12)})}{(\frac{0.03}{12})}[/latex] = $11,130.47 So Abigale can afford a $11,130.47 loan. She will pay a total of $12,000.00 ($200.00 per month for 60 months) to the loan company. The difference between the amount she pays and the amount of the loan is the interest paid. In this case, Abigale is paying $12,000 – $11,130.47 = $869.53 interest total. |
You can also use TVM Solver to do this calculation.
| Example 3 – Repeat of Example 2 Using the TVM Solver |
| Abigale can afford $200.00 per month as a car payment. If she can get an auto loan at 3% interest for 60 months (5 years), how expensive of a car can she afford (in other words, what amount loan can she pay off with $200.00 per month)? |
|
In this example, we are looking for PV, the starting amount of the loan. Using TVM Solver: N = 12*5 Once all of the given parameters are entered in, solve for PV= to get PV = 11,130.47153 So Abigale can afford a car loan of up to $11,130.47. |
You can also use the formula or TVM solver to calculate what your loan payment will be for a given amount you are borrowing.
| Important Note About Rounding When Calculating Loan Payments: |
|
Always round the loan payment UP to the nearest cent. This means that if your loan payment answer is $138.420000001 then your final loan payment answer should be $138.43. You have to follow this unconventional rounding rule when calculating loan payments. If you had rounded down, then you will come up short on your loan at the end of the term. A payment of $138.42 is not enough to pay off the loan in the given time period (term). You might be thinking that this means you would actually overpay your lender and you are RIGHT! In the real world you have to contact the lender to determine the amount for your last payment. If you have ever paid off a car or mortgage, this is the mathematical reason why your last payment is typically different than your regular payment. |
| Example 4 |
| You want to take out a $140,000.00 mortgage (home loan). The interest rate on the loan is 6%, and the loan is for 30 years. How much will your monthly payments be? |
|
Using TVM Solver: N = 12*30 Once all of the given parameters are entered in, solve for PMT= PMT = -839.37073 So you will make payments of $839.38 per month for 30 years. (Note that you went up to 38 cents even though normal rounding rules would say to leave it at 37 cents) You’re paying a total of $302,176.80 to the loan company ($839.38 per month for 360 months). You are paying a total of $302,176.80 – $140,000 = $162,176.80 in interest over the life of the loan. |
| You Try PF.12.A |
| Janine bought $3,000.00 of new furniture on credit. Because her credit score isn’t very good, the store is charging her a fairly high interest rate on the loan: 16%. If she agreed to pay off the furniture over 2 years, how much will she have to pay each month? |
With loans, it is often desirable to determine what the remaining loan balance will be after some number of years. For example, if you purchase a home and plan to sell it in five years, you might want to know how much of the loan balance you will have paid off and how much you have to pay from the sale.
Remember that only a portion of your loan payments go towards the loan balance; a portion is going to go towards interest. For example, if your payments were $1,000.00 a month, after a year you will not have paid off $12,000.00 of the loan balance.
| Example 5 (Continued from Example 4) |
| You want to take out a $140,000.00 mortgage (home loan). The interest rate on the loan is 6%, and the loan is for 30 years. Your monthly payments are $839.38. How much will still be owed after making payments for 10 years? |
|
Using TVM Solver: N = 12*10 Once all of the given parameters are entered in, solve for FV. FV = -117,158.50 So you will still owe $117,158.50 after making payments for 10 years. |
| You Try PF.12.B |
| You finance a $30,000.00 car at 2.9% interest for 60 months (5 years). What will your monthly payments be? How much will you still owe on the car after making payments for 2 years? |
In the real world getting a loan to buy a home (mortgage) is a little more complicated than the examples above. Your lender will often require a down payment in order to qualify for the loan. A down payment is a percentage of the value of the home you are buying. A 20% down payment will allow you to avoid being required to pay Private Mortgage Insurance (PMI) every month. In addition to may have to pay for points in order to reduce your interest rate. A point in a one-time fee that is equal to 1% of your loan amount. You may need to pay for multiple points and this fee is not applied to your loan balance. Let’s put all these concepts together in the next example.
| Example 6 |
| The cost of a home you want to purchase is $160,000.00. To qualify for a mortgage, your lender wants a 15% down payment. Your mortgage interest rate is 5% for 30 years and you have to pay two points. |
0.15 * $160,000 = $24,000 The required down payment is $24,000.00
$160,000 – $24,000 = $136,000.00 is the amount you are borrowing.
Each point costs 1% of the value of your mortgage. 0.01 * $136,000 = $1,360.00 is the cost for one point You will have to pay 2 * $1,360 = $2,720.00 for the two points.
Using TVM Solver: N = 12 * 30 Once all of the given parameters are entered in, solve for PMT. PMT = -730.07740… So your monthly mortgage payment will be $730.08
By the end of your loan you will have made 12*30 = 360 payments. This means the total of all your payments is 360*$730.08 = $262,828.80
You borrowed $136,000.00 and paid $262,828.80 to pay off the loan. The difference between these numbers is the total interest you paid on your loan. $262,828.80 – $136,000 = $126,828.80 You paid almost as much in interest as your original loan! You can really see how the interest piled up over 30 years. |
Few people stay in their home for 30 years. It is important to understand that your down payment and a portion of your mortgage payment go towards the equity in the home. The equity in your home is the difference between the current value and the current balance of your mortgage.
Equity = (Current Value) – (Current Loan Balance)
An amortization table shows how each monthly payment reduces your current loan balance.
| Example 7 (continued from Example 6) | ||||||||||||||||||||
|
Construct the first three months of an amortization table for the mortgage in Example 6. Month 1: Each month the interest is calculated using the simple interest formula, I = P0rt, where P0 is the principal, r is the annual interest rate, and t is the time in years. Banks follow normal rounding rules when calculating interest, always rounding to the nearest cent. Interest on Prior Balance = $136,000 * 0.05 * (1 month) Time must be in years Ending Balance = (Prior Balance) + (Interest on Prior Balance) – (Payment) = $136,000 + $566.67 – $730.08 = $135,836.59 Month 2: Interest on Prior Balance = $135,836.59 * 0.05 * 112 = $565.98579… = $565.99 Ending Balance = $135,836.59 + $565.99 – $730.08 = $135,672.50 Month 3: Interest on Balance = $672.50 * 0.05 * 112 = $565.300208… = $565.30 Ending Balance = $135,672.50 + $565.31 – $730.08 = $135,507.73 The completed table is below.
Notice that the amount of each payment that is applied to the principal (balance) slowly increases each month. Towards the end of your loan your payment will almost entirely apply to the principal. |
Section PF.12 – Answers to You Try Problems
PF.12.A
She will have to pay $146.89 each month.
PF.12.B
Monthly payments: $537.73 per month
You will still owe $18,518.61 after 2 years.
