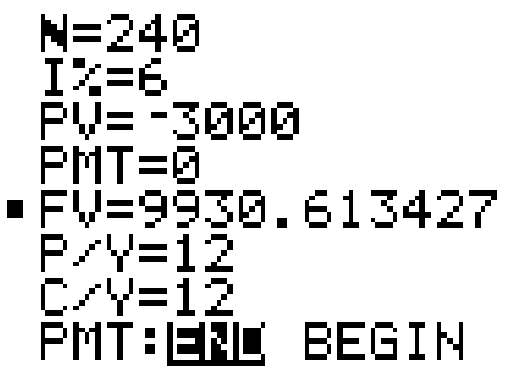Section PF.8 – Compound Interest
With simple interest, we were assuming that we pocketed the interest when we received it. In a standard bank account, any interest we earn is automatically added to our balance, and we earn interest on that interest in future years. This reinvestment of interest is called compounding.
Suppose that we deposit $1,000.00 in a bank account offering 3% interest, compounded monthly. How will our money grow?
The 3% interest is an annual percentage rate (APR) – the total interest to be paid during the year. Since our interest is being paid monthly, each month we will earn [latex]\frac{1}{12}[/latex] of the 3% annual interest, or [latex]\frac{3}{12}[/latex]% = 0.25% per month.
In the first month,
P0 = $1,000
r = 0.0025 (0.25%)
I = $1,000 (0.0025) = $2.50
A = $1,000 + $2.50 = $1,002.50
In the first month, we will earn $2.50 in interest, raising our account balance to $1,002.50.
In the second month,
P0 = $1,002.50
I = $1,002.50 (0.0025) = $2.51 (rounded)
A = $1,002.50 + $2.51 = $1,005.01
Notice that in the second month we earned more interest than we did in the first month. This is because we earned interest not only on the original $1,000 we deposited, but we also earned interest on the $2.50 of interest we earned the first month. This is the key advantage that compounding of interest gives us.
Calculating out a few more months (rounding to the nearest cent):
|
Month |
Starting balance |
Interest earned |
Ending Balance |
|
1 |
1,000.00 |
2.50 |
1,002.50 |
|
2 |
1,002.50 |
2.51 |
1,005.01 |
|
3 |
1,005.01 |
2.51 |
1,007.52 |
|
4 |
1,007.52 |
2.52 |
1,010.04 |
|
5 |
1,010.04 |
2.53 |
1,012.57 |
|
6 |
1,012.57 |
2.53 |
1,015.10 |
|
7 |
1,015.10 |
2.54 |
1,017.64 |
|
8 |
1,017.64 |
2.54 |
1,020.18 |
|
9 |
1,020.18 |
2.55 |
1,022.73 |
|
10 |
1,022.73 |
2.56 |
1,025.29 |
|
11 |
1,025.29 |
2.56 |
1,027.85 |
|
12 |
1,027.85 |
2.57 |
1,030.42 |
The standard formula for compound interest is as follows:
| Compound Interest |
|
A = P0(1 + [latex]\frac{r}{n}[/latex])nt A is the balance in the account after t years t is the number of years we plan to leave the money in the account P0 is the balance in the account at the beginning (starting amount, or principal). r is the annual interest rate (APR) in decimal form (Example: 5% = 0.05) n is the number of compounding periods in one year. If the compounding is done annually (once a year), n = 1. |
The most important thing to remember about using this formula is that it assumes that we put money in the account once and let it sit there earning interest.
| Example 1 |
|
If you invest $3,000.00 in an investment account paying 3% interest compounded quarterly, how much will the account be worth in 10 years? Since we are starting with $3,000, P0 = 3,000 Our interest rate is 3%, so r = 0.03 Since we are compounding quarterly, we are compounding 4 times per year, so n = 4 We want to know the value of the account in 10 years, so we are looking for the ending value, A, when t = 10. A = 3,000(1 + [latex]\frac{0.03}{4}[/latex])4(10) = $4,045.05 The account will be worth $4,045.05 in 10 years. |
| You Try PF.8.A |
| If you invest $3,000.00 in an investment account paying 3% interest compounded weekly, how much will the account be worth in 10 years? |
| Example 2 | ||||||||||||||||||||||||
|
A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3,000.00 in a CD paying 6% interest, compounded monthly. How much will you have in the account after 20 years? In this example, The initial deposit, P0 = $3,000 6% annual rate, r = 0.06 12 months in 1 year, n = 12 Since we’re looking for how much we’ll have after 20 years, t = 20 So A = 3,000(1 + [latex]\frac{0.06}{12}[/latex])12(20) = $9,930.61 (round your answer to the nearest penny) Let us compare the amount of money earned from compounding against the amount you would earn from simple interest:
|
| Example 3 |
| A 529 plan is a college savings plan in which a relative can invest money to pay for a child’s later college tuition, and the account grows tax free. If Lily wants to set up a 529 account for her new granddaughter, wants the account to grow to $40,000.00 over 18 years, and she believes the account will earn 6% compounded semi-annually (twice a year), how much will Lily need to invest in the account now? |
|
Since the account is earning 6%, r = 0.06 Since interest is compounded twice a year, n = 2 In this problem, we don’t know how much we are starting with, so we will be solving for P0, the initial amount needed. We do know we want the end amount, A, to be $40,000, so we will be looking for the value of P0 so that A= 40,000. 40,000 = P0(1 + [latex]\frac{0.06}{2}[/latex])2(18) 40,000 = P0(2.898278328) P0 = [latex]\frac{40,000}{2.898278328}[/latex] = $13,801.30 (round your answer to the nearest penny) Lily will need to invest $13,801.30 to have $40,000.00 in 18 years. |
| A Note on Rounding |
|
It is important to be very careful about rounding when performing calculations. If possible, enter the entire calculation in one step into your calculator to avoid rounding error. If this is not possible, you want to keep as many decimals during calculations as you can. Try calculating example 5 using 2.898 instead of and compare your answer with the example. The general rule is… Don’t Round Early |
| You Try PF.8.B |
| If Lily wants to set up a 529 account for her new granddaughter, wants the account to grow to $40,000 over 18 years, and she believes the account will earn 6% compounded daily, how much will Lily need to invest in the account now? |
In the previous examples, you were shown how to work on the problems using the formula. The TVM Solver program on your graphing calculator can perform these calculations for you, and much quicker! The guide on the next page will introduce you to using the TVM solver with compounding interest problems.
| Using the TVM Solver on your TI - Graphing Calculator |
|
Press APPS, then Finance, and TVM Solver (Note: If you have an older TI-83 calculator and do not have an APPS key, look for a key labeled Finance.) You will see a screen like the following: (Note: You will see different numbers after each parameter. There’s no reason to reset to zero--you will type right over them.)
N: Total number of payment/compounding periods (this is n*t where n is the number of compounding per year and t is the time in years) I%: Annual interest rate (APR) (Entered as a percent, NOT as a decimal.) PV: Present Value (the principal or beginning amount) PMT: Payment Amount (must be equal regular payments) FV: Future Value (accumulated value or end amount) P/Y: Number of payment periods per year C/Y: Number of compounding periods per year 'PMT:' For this class, keep the setting on END, indicating end-of-the month payments. For our applications, C/Y will always be the same value as P/Y. If you change P/Y, your calculator will automatically reset C/Y. NOTES:
TVM Solver will calculate the value of ANY of the first five values in the above list (N, I%, PV, PMT or FV) if the other four values are known. To solve for an unknown value, you will put the curser on the line you wish to find and then press SOLVE (press ALPHA, then the ENTER key). |
| Example 4 – Repeat of Example 2 using the TVM Solver |
|
A certificate of deposit (CD) is a savings instrument that many banks offer. It usually gives a higher interest rate, but you cannot access your investment for a specified length of time. Suppose you deposit $3,000.00 in a CD paying 6% interest, compounded monthly. How much will you have in the account after 20 years? |
|
N = 20*12 (20 years times 12 months for compounded monthly) Once all of the given parameters are entered in, move your cursor to FV= and press ALPHA – ENTER. FV = 9930.613427 so the future value (ending balance) will be $9,930.61. |
| Example 5 – Repeat of Example 3 using the TVM Solver |
| A 529 plan is a college savings plan in which a relative can invest money to pay for a child’s later college tuition, and the account grows tax free. If Lily wants to set up a 529 account for her new granddaughter, wants the account to grow to $40,000.00 over 18 years, and she believes the account will earn 6% compounded semi-annually (twice a year), how much will Lily need to invest in the account now? |
|
N = 18*2 (18 years times 2 for compounded twice a year) Once all of the given parameters are entered in, move your cursor to PV= and press ALPHA – ENTER. PV = -13,801.297 so the present value (amount Lily needs to deposit) will be $13,801.30. |
Section PF.8 – Answers to You Try Problems
PF.8.A
The account will be worth $4,049.23.
PF.8.B
Lily will need to invest $13,585.03 to have $40,000.00 in 18 years.

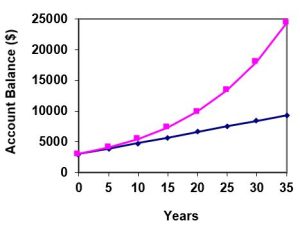 As you can see, over a long period of time, compounding makes a large difference in the account balance. You may recognize this as the difference between linear growth and exponential growth.
As you can see, over a long period of time, compounding makes a large difference in the account balance. You may recognize this as the difference between linear growth and exponential growth.