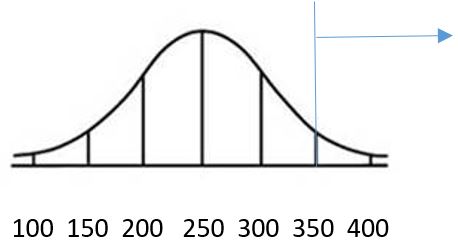
Section S.6 – Solutions to the Practice Problems
1. A z-score measures the number of standard deviations above or below the mean a particular observation lies.
2. 0; 1
3. z = 2
4. z = -1.5
5. z = 2.78
6. z = -0.133
7. z = 1.5
8. z = -1.67
9. z = 0
10. z = -0.33
11. 1.25; left
12. 0.67; right
13. 6; right
14. 3.14; left
15. 1.7; left
16. z = -0.85
17.
a. z = -0.51. A basketball player who is 77 inches tall is 0.51 standard deviations below the mean height of 79 inches.
b. z = 1.54. A basketball player who is 85 inches tall is 1.54 standard deviations above the mean height of 79 inches.
18.
a. Blood pressure of 100: z = -1.79, Blood pressure of 150: z = 1.79
b. I would tell my friend that if his systolic blood pressure was 2.5 standard deviations below the mean, it would be 90. As we just calculated in part a) systolic blood pressure between 100 and 150 actually corresponds to between 1.79 standard deviations below the mean and 1.79 standard deviations above the mean.
19. x = 20
20. x = 5.75
21. x = 1
22. x = 8
23. 1.5 years
24.
a. An NBA player with a z-score of 3.5 would be 92.62 inches tall. That is just over 7 feet, 8 inches tall. While that height is possible, it’s not very likely since it is more than 3 standard deviations above the mean. I probably would not believe him.
b. An NBA player with a z-score of -3.5 would be 65.39 inches tall. That is just over 5 feet, 5 inches tall, which is less than 3 standard deviations below the mean. I would probably not believe him.
25.
a. A man with a z-score of 0.75 has a systolic blood pressure of 135.5. This is not an unusual blood pressure, as it’s only 0.75 standard deviations more than the average blood pressure of 125.
b. A man with a z-score of 3.2 has a systolic blood pressure of 169.8. This is an unusual blood pressure, since it is more than 3 standard deviations above the mean.
26. 1 – 0.123 = 0.877
27. 1 – 0.543 = 0.457
28.
a. 0.0968
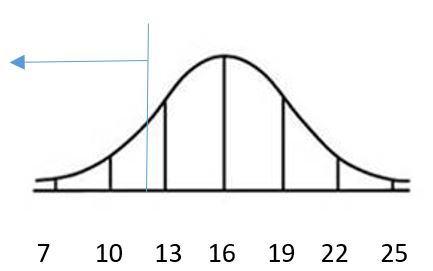
b. 0.9032
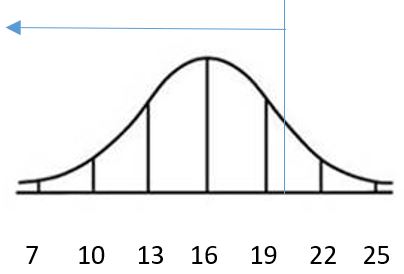
c. 0.6368
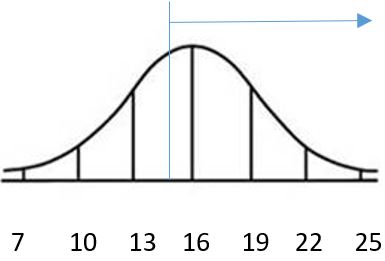
d. 0.0035
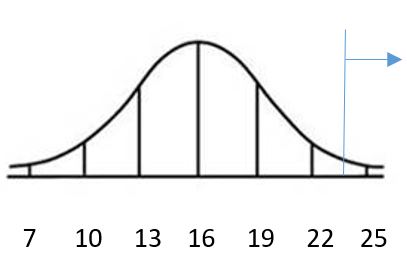
e. 0.8064
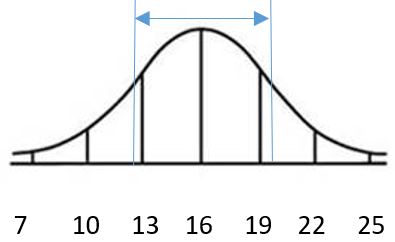
29.
a. 0.0968
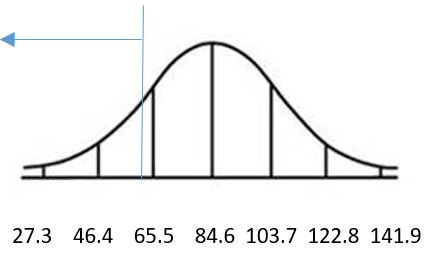
b. 0.9032
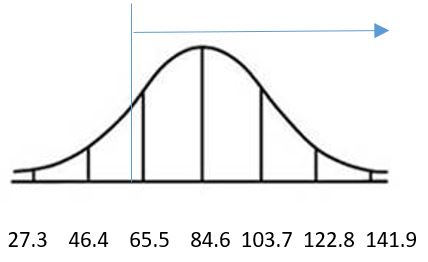
c. 0.9893
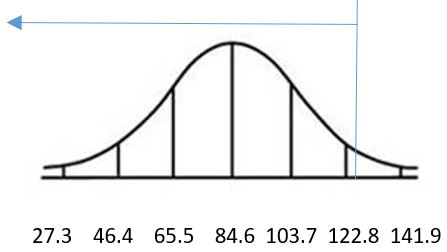
d. 0.0359
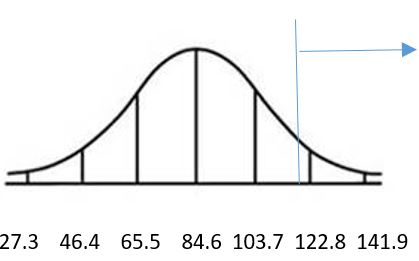
e. 0.0192
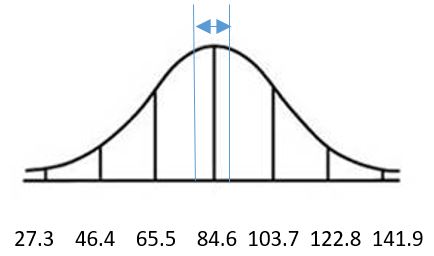
30.
a. 0.00003
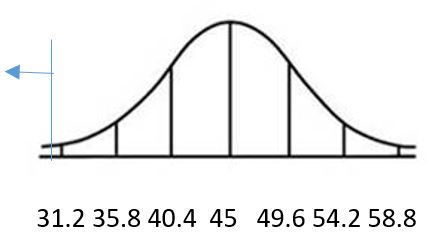
b. 0.5000
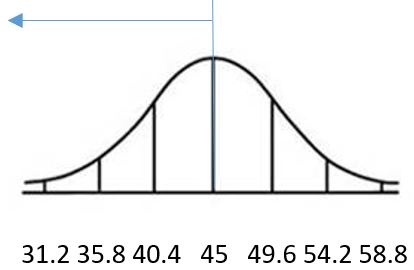
c. 0.0668
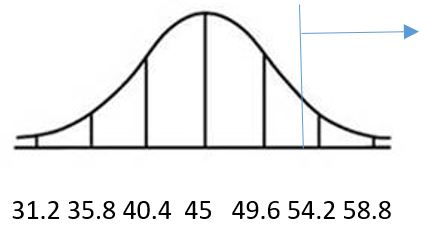
d. 0.9332
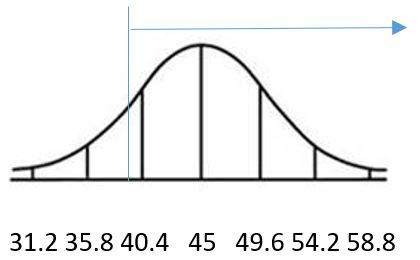
e. 0.7375
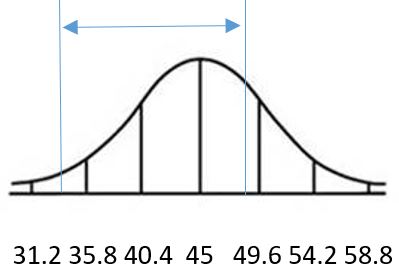
31.
a. 0.0580
b. 0.9420
c. 0.0126
32.
a. 0.5404
b. An adult Asian male who is 72 inches tall has a z-score of 2.4. The proportion of values greater than z = 2.4 is 0.0082. That means that it would be fairly unusual to see an adult Asian male who is over 72 inches tall (only about 0.82% of adult Asian males are over 72 inches tall).
33.
a. 0.0912
b. 0.0038
34.
a. 0.3446
b. 0.0501
35.
a. 0.2743
b. 0.0228