10 Compounds with More Than One Chirality Center
Chapter 10 Learning Objectives
- Be able to draw diastereomers for a given chiral compound.
- Be able to distinguish between enantiomers, diastereomers and meso compounds.
10.1 Diastereomers
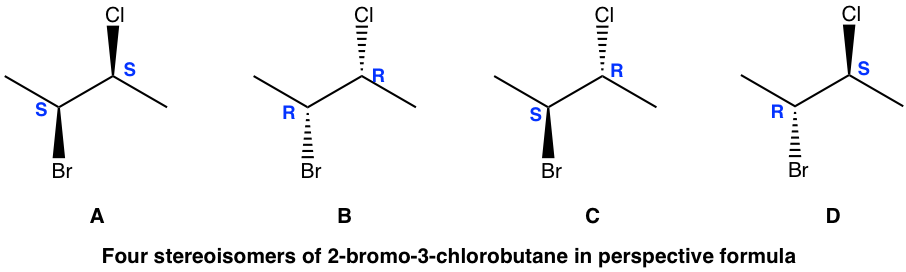
It is very common that there are more than one chirality center in an organic compound. For the example of 2-bromo-3-chlorobutane below, there are 2 chirality centers, C2 and C3. With each chirality center has two possible configurations, R and S, the total number of possible stereoisomers for this compound is four, with configurations on C2 and C3 as (R,R), (S,S), (R,S) and (S,R) respectively.

As a general rule, for a compound has n chirality centers, the maximum number of stereoisomers for that compound is 2n.
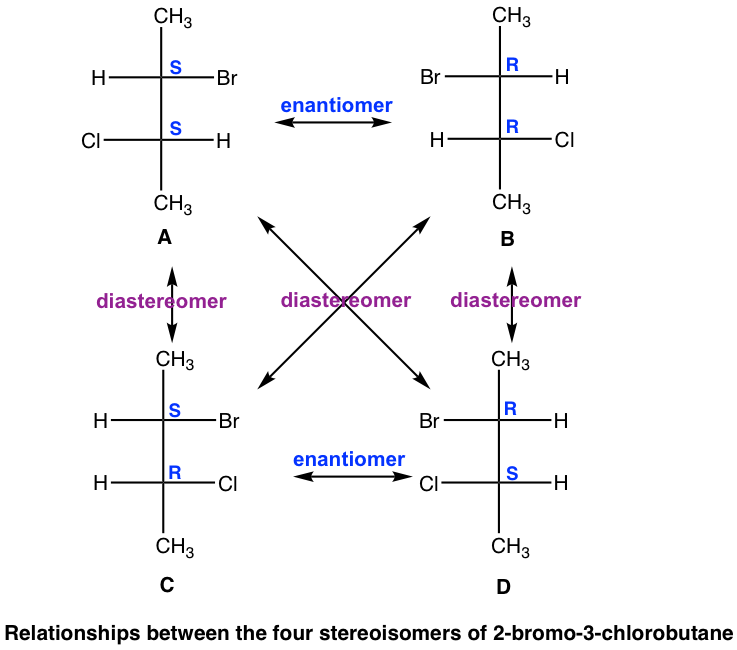
The four stereoisomers of 2-bromo-3-chlorobutane consist of two pairs of enantiomers. Stereoisomers A and B are a pair of non-superimposable mirror images, so they are enantiomers. So are the isomers C and D. Then what is the relationship between isomer A and C?
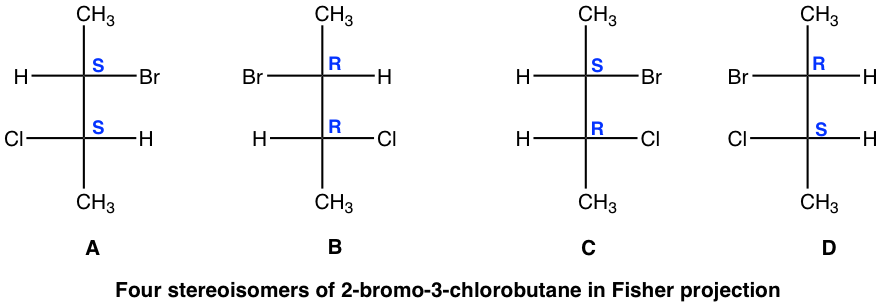
A and C are not identical, not enantiomers, and they are stereoisomers (have the same bonding but differ in the spatial arrangement of groups). Such type of stereoisomers are defined as diastereomers. Diastereomers are stereoisomers that are not enantiomers. For the four stereoisomers here, there are four pairs of diastereomers: A and C, A and D, B and C,B and D. The relationship between the four stereoisomers can be summarized as:
The stereoisomer then has two sub-types, enantiomers and diastereomers, because any stereoisomers that are not enantiomers can always be called diastereomers. Based on such definition, the geometric isomers we learned earlier also belong to the diastereomer category.
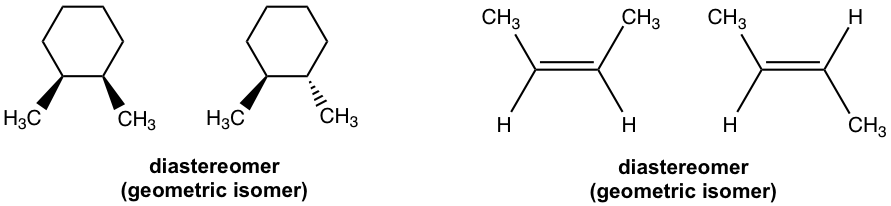
As mentioned earlier, enantiomers are very alike to each other, and they share same physical properties except optical activity (opposite sign for specific rotation). Enantiomers also generally have same chemical properties, except the reaction with other chiral reagents (not topics in this course).
However, diastereomers are not that closely related. Diastereomers have different physical properties, for example, different b.p, color, density, polarity, solubility etc. They also have different chemical properties.
Next, we will go through the examples of cyclic compounds, to see how the new concept of diastereomer relates to the knowledge about cyclic compounds we learned before.
Examples
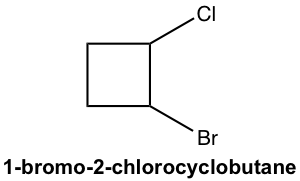
Approach:
There are two chirality centers for 1-bromo-2-chlorocyclobutane molecule. So the maximum number of stereoisomer is four. To work on the stereoisomers for cyclic compound, we can start with cis/trans isomer, and then check does the enantiomer apply to each case.
Solution:
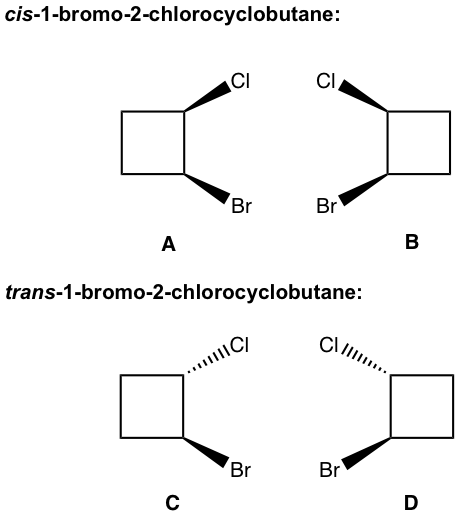
There are two cis-isomers, A and B, and they are enantiomers of each other; similarly, there are also two trans-isomers C and D that are enantiomers of each other as well.
The relationship between any of the cis-isomer to any of the trans-isomer is diastereomers (A and C, A and D, B and C, B and D). Since they are geometric isomers, and remember that the geometric isomers can also be called diastereomers.
All geometric isomers are diastereomers (it is always correct to call a pair of geometric isomers as diastereomers), however not all the diastereomers are geometric isomers!
Examples:
What is the relationship between the following pair of compounds, enantiomers, identical, diastereomers, constitutional isomers, non-isomers?
1.
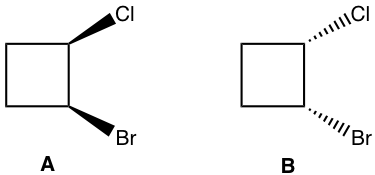
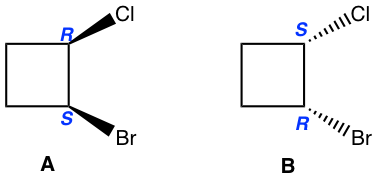
Method I: The basic way is to determine the configuration of each chirality center. As shown below that the configuration for both chirality centres are right opposite between the structure A and B. So they are enantiomers.
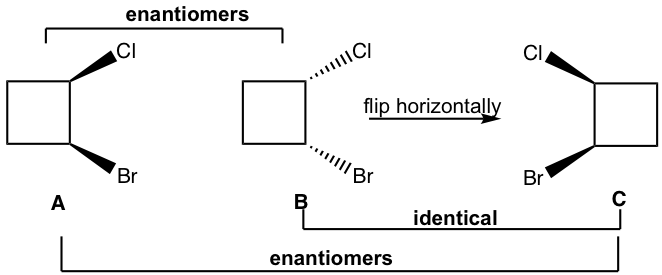
Method II: For the cyclic structures, sometimes rotate or flip a given structure in a certain way helps us to tell the relationship (using the molecular model helps the rotate or flip part). For this example, flipping structure B horizontally leads to structure C, B and C are identical. Then it is easy to tell that A and C are just non-superimposable mirror images to each other, so A and C are enantiomers, then A and B are enantiomers as well.
If this method looks confusing to you, then you can stick to Method I.
2.
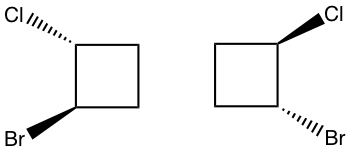
You can use either of the above methods, the answer is “identical”.
10.2 Meso compound
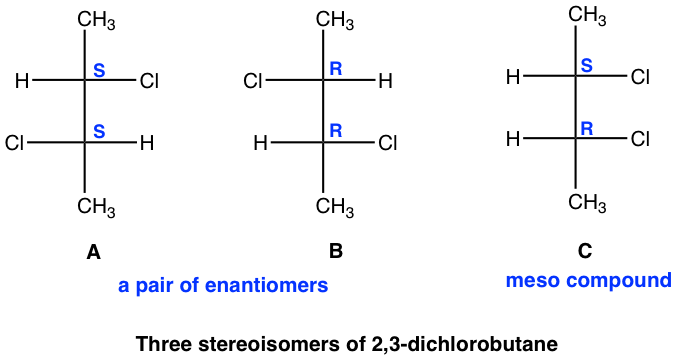
Next, we will see another example of a compound containing two chirality centers, 2,3-dichlorobutane, the compound that has the same substituents on C2 and C3 carbons.

Theoretically, there are maximum four stereoisomers, the structures are shown by Fisher projections here.

Stereoisomer A and B are non-superimposable mirror images, so they are enantiomers.
We will take a detailed look at stereoisomer C and D. Yes, they are mirror images, but are they really non-superimposable? If isomer C is rotated 180° (180° rotation still get the same structure back for Fisher projection), then it could get superimposed on isomer D. So, isomer C and D are superimposable mirror images, that means they are the same, identical!
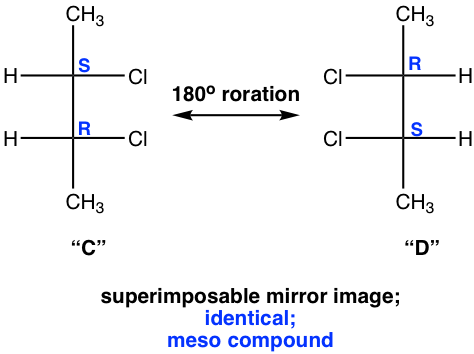
Then “C” and “D” are just different drawings for the same stereoisomer. The next questions is, is this stereoisomer chiral? We have confirmed that this isomer does get superimposed on its mirror image, that means it is achiral.
This is so weird! How come a compound that contain two chirality centers (C2 and C3) is achiral?
Yes, it does happen! A compound that is achiral but contain chirality centers is called meso compound. A meso compounds is achiral and optical inactive (does NOT rotate the plane of polarization of plan-polarized light), but it does have multiple chirality centers.
Because that one stereoisomer is meso compound, the total number of stereoisomers for 2,3-dichlorobutane is three.
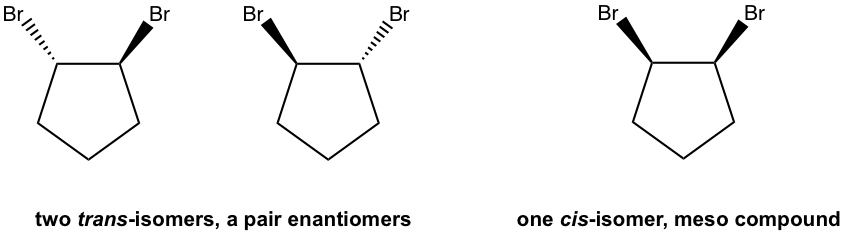
Examples: Draw all the stereoisomers of 1,2-dibromocyclopentane.
Solutions: there are total three stereoisomers.
Exercises 10.1
- Draw all stereoisomers for 1-ethyl-3-methylcyclohexane.
- Draw all stereoisomers for 1-ethyl-4-methylcyclohexane.
- Draw all stereoisomers for 1,2-dimethylcyclohexane.
10.3 Determination of Chirality from Plane of symmetry
The existence of chirality centers does not guarantee the chirality of a molecule, for example of the meso compound. Following the definition of chirality always involve the comparison between original structure and its mirror image, that needs extra work. Is there any easier way to tell whether a moleculeis chiral or achiral?
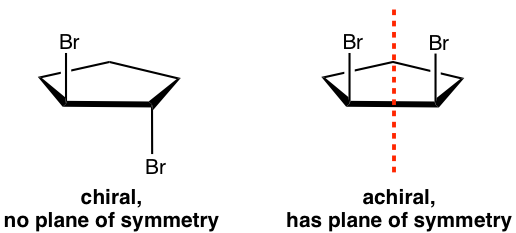
We can check the plane of symmetry. Plane of symmetry is a plane that cuts the molecule in half and that one half is the mirror image of the other.
- If a molecule does have a plan of symmetry, then the molecule is achiral.
- The molecule that does not have a plane of symmetry in any conformation is chiral.
For the meso isomer of 2,3-dichlorobutane, the plane of symmetry is the plane that is labelled in the structure below.

Examples:

Solution:
Examples: What is the relationship of the following pair of structures?
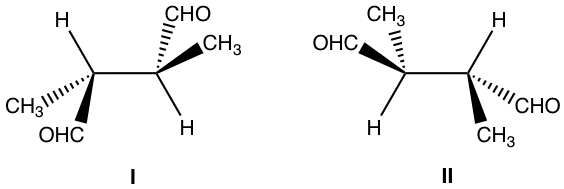
Approach: Determine the R/S configuration of each carbon.
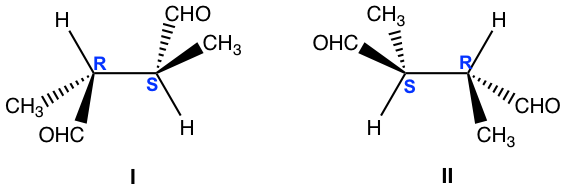
For both structures, the chirality centres are bonded with the same groups, and structure I has R and S, structure II has S and R. Are they enantiomers?
A bit further investigation is necessary to get the conclusion. Let’s rotate the groups around the 2nd chirality centre of structure I (you can use the molecular model to do the rotation, that is very helpful for visualizing the spatial arrangement of the groups):

Rotation of the groups around the chirality centre does not change the configuration, however it does change the conformation to eclipsed conformation. In the eclipsed conformation, it is easier to tell that the structure has a plane of symmetry, so it is a meso compound that is achiral. Achiral compound does not have enantiomer, so structure II is also meso compound that is identical to structure I.
Solution: Identical
(You can rotate, or do switches to compare between the two structures, but make sure to keep track on any action. If it is easy to get lost by rotating or switch, assign R/S configuration is a safer way.)
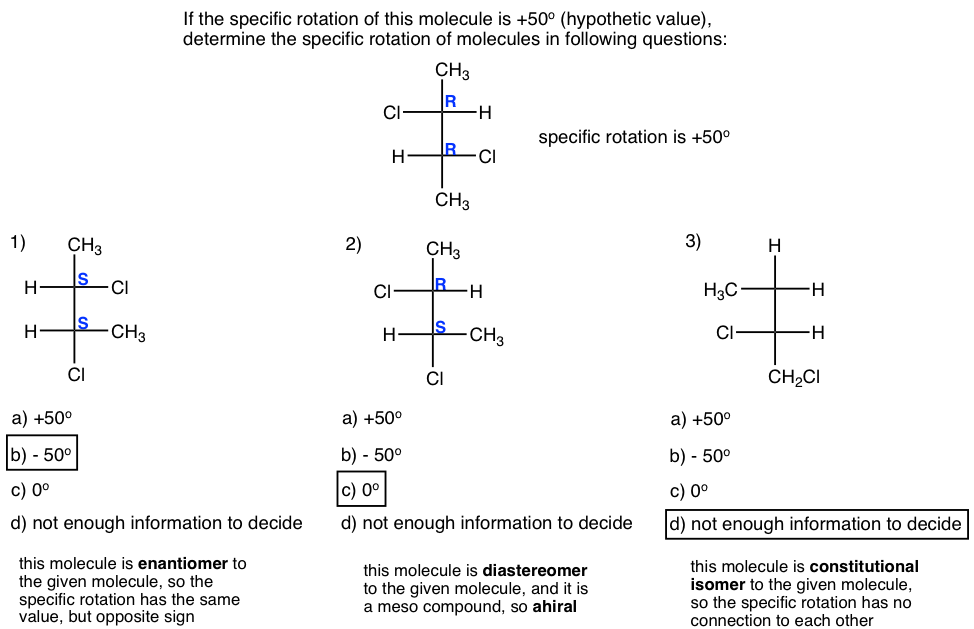
Examples
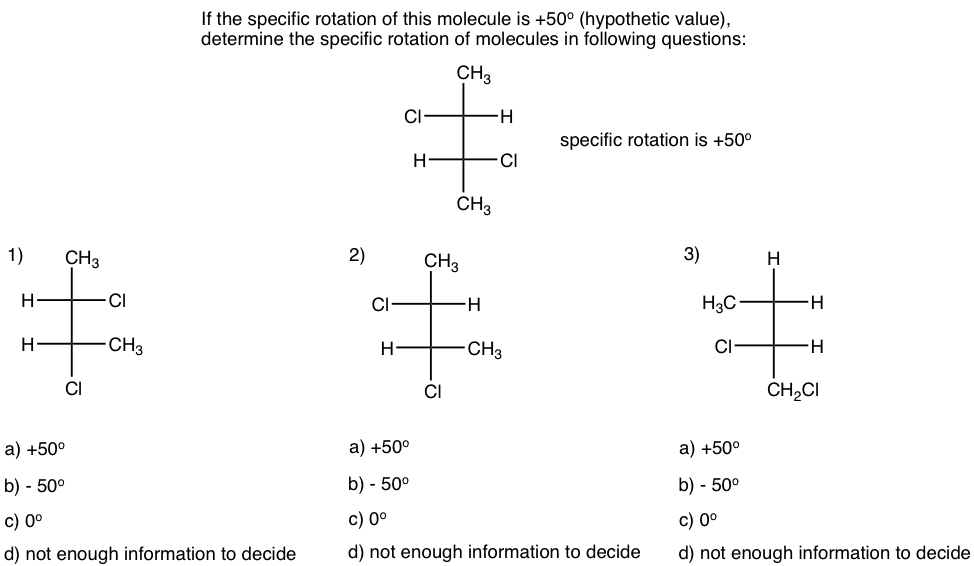
Thinking: Determine the relationship between the molecule in each question with the given one, and apply the knowledge of specific rotation.
Solutions: