18 Conformational Analysis of Alkanes
Chapter 18 Learning Objectives
-
Draw and analyze Newman projections of alkanes (e.g., butane) and explain the relative stability of conformers (e.g., anti, gauche).
-
Use potential energy diagrams to describe conformational changes in alkanes.
- Be able to calculate the strain energy of a given conformation.
Stereochemistry is the branch of chemistry concerned with the three-dimensional aspects of molecules.We’ll see on many occasions in future chapters that the exact three-dimensional structure of a molecule is often crucial to determining its properties and biological behavior. We already know that σ bonds are cylindrically symmetrical. In other words, the intersection of a plane cutting through a carbon–carbon single-bond orbital looks like a circle. Because of this cylindrical symmetry, rotation is possible around carbon–carbon bonds in open-chain molecules. In ethane, for instance, rotation around the C–C bond occurs freely, constantly changing the spatial relationships between the hydrogens on one carbon and those on the other.
The different arrangements of atoms that result from bond rotation are called conformations, and molecules that have different arrangements are called conformational isomers, or conformers. Unlike constitutional isomers, however, different conformers often can’t be isolated because they interconvert too rapidly.
18.1 Conformations of Alkanes
Carbon-carbon single bonds can rotate freely in space. The different arrangements obtained by the rotation of C-C single bonds are known as conformations. Molecules that have different conformations are known as conformers or conformational isomers. Here are two conformations of ethane. There are many more possible conformations.
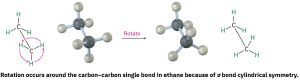
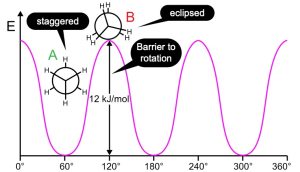
Figure 18.1: Conformations of Ethane
Credits: https://commons.wikimedia.org/
Although there are many conformations, only two are of interest here. These are the eclipsed and staggered conformations. In the eclipsed conformations, all C-H bonds and C-C bonds eclipse each other. Due to close proximity of the bonds, electrons in the bonds are involved in unfavorable interactions. These interactions lead to an increase in the energy of the eclipsed conformation, thereby, reducing its stability. In the staggered conformation, the bonds are as far away as the molecular geometry allows. A molecule in the staggered conformation experiences minimum repulsions. Therefore, this conformation has the minimum energy. Rotation of C-C single bonds take very little energy and therefore a staggered conformation will convert into an eclipsed conformation and vice versa. In other words, a molecule cannot avoid an eclipsed conformation even though the energy of this conformation is higher than the staggered conformations. However, the molecule may not spend much time in an eclipsed conformation. For ethane, the conversion from a staggered conformation to eclipsed conformation requires 12 kJ/mol. This energy difference is known as barrier to rotation.
Conformations are often represented using the Newman projection formulas. Conformational isomers can also be represented by sawhorse drawings. A sawhorse representation views the carbon–carbon bond from an oblique angle and indicates spatial orientation by showing all C–H bonds. A Newman projection views the carbon–carbon bond directly end-on and represents the two carbon atoms by a circle. Bonds attached to the front carbon are represented by lines to the center of the circle, and bonds attached to the rear carbon are represented by lines to the edge of the circle.
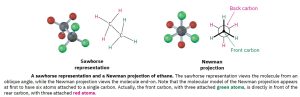
Figure 18.2: Newman and Sawhorse Diagrams of Staggered Conformation of Ethane
Visit the following resources to gain a good understanding of drawing and interpreting Newman formulas.
- What is Newman projection formula? View this video that is part of a series of videos on Newman projections. (Part 1)
- View this video that explains the Newman projection of substituted propanes (Part 3)
Propane, the next-higher member in the alkane series, also has a torsional barrier that results in hindered rotation around the carbon–carbon bonds. The barrier is slightly higher in propane than in ethane—a total of 14 kJ/mol (3.4 kcal/mol) versus 12 kJ/mol. The eclipsed conformation of propane has three interactions—two ethane-type hydrogen–hydrogen interactions and one additional hydrogen–methyl interaction. Since each eclipsing H⟷H interaction is the same as that in ethane and thus has an energy “cost” of 4.0 kJ/mol, we can assign a value of 14 – (2 × 4.0) = 6.0 kJ/mol (1.4 kcal/mol) to the eclipsing H⟷CH3 interaction.
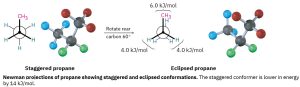
Figure 18.3: Rotation of Staggered to Eclipsed Conformations of Ethane
The conformational situation becomes more complex for larger alkanes because not all staggered conformations have the same energy and not all eclipsed conformations have the same energy.
View this video that explains the Newman projection of butane. (Part 2)
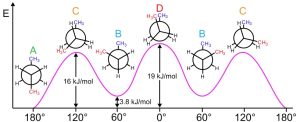
In butane, for instance, the lowest-energy arrangement, called the anti conformation, is the one in which the two methyl groups are as far apart as possible—180° away from each other. As rotation around the C2–C3 bond occurs, an eclipsed conformation is reached where there are two CH3⟷H interactions and one H⟷H interaction. Using the energy values derived previously from ethane and propane, this eclipsed conformation is more strained than the anti conformation by 2 × 6.0 kJ/mol + 4.0 kJ/mol (two CH3⟷H interactions plus one H⟷H interaction), for a total of 16 kJ/mol (3.8 kcal/mol).
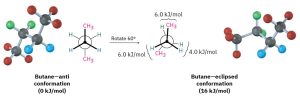
Figure 18.4: Rotation of Anti to Eclipsed Conformations of Butane
As bond rotation continues, an energy minimum is reached at the staggered conformation where the methyl groups are 60° apart. Called the gauche conformation, it lies 3.8 kJ/mol (0.9 kcal/mol) higher in energy than the anti conformation even though it has no eclipsing interactions. This energy difference occurs because the hydrogen atoms of the methyl groups are near one another in the gauche conformation, resulting in what is called steric strain. Steric strain is the repulsive interaction that occurs when atoms are forced closer together than their atomic radii allow. It’s the result of trying to force two atoms to occupy the same space.
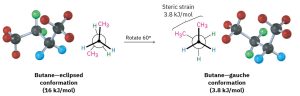
Figure 18.5: Rotation of Eclipsed to GaucheConformation of Butane
As the dihedral angle between the methyl groups approaches zero, an energy maximum is reached at a second eclipsed conformation. Because the methyl groups are forced even closer together than in the gauche conformation, both torsional strain and steric strain are present. A total strain energy of 19 kJ/mol (4.5 kcal/mol) has been estimated for this conformation, making it possible to calculate a value of 11 kJ/mol (2.6 kcal/mol) for the CH3⟷CH3 eclipsing interaction: total strain of 19 kJ/mol minus the strain of two H⟷H eclipsing interactions (2 × 4.0 kcal/mol) equals 11 kJ/mol.
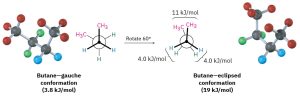
Figure18.6: Rotation of Gauche to Eclipsed Conformation of Butane
After 0°, the rotation becomes a mirror image of what we’ve already seen: another gauche conformation is reached, another eclipsed conformation, and finally a return to the anti conformation. A plot of potential energy versus rotation about the C2–C3 bond is shown in the following figure.
Figure 18.7: Conformational Analysis of Butane
Credits: https://commons.wikimedia.org/
The notion of assigning definite energy values to specific interactions within a molecule is very useful. A summary of what we’ve seen thus far is given in the table below.
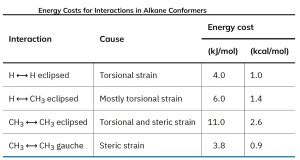
Table 18.1: Energy Costs for Interactions in Alkane Conformations
The same principles just developed for butane apply to pentane, hexane, and all higher alkanes. The most favorable conformation for any alkane has the carbon–carbon bonds in staggered arrangements, with large substituents arranged anti to one another.
- This video gives a brief account of estimating torsional and steric strain from Newman projections of alkanes.
- For a brief overview of the conformational analysis of alkanes, visit this site.
Key Takeaways
- Alkanes can rotate about single bonds and attain various conformations.
- Staggered conformations are more stable than eclipsed conformation.
- Torsional and steric strain are the reasons for increase in potential energy for certain conformations.
- Anti staggered is the most stable conformation where the dihedral angle separating the most bulky groups is 1800.
- The energy difference between the most stable and the least stable conformations is known as the barrier to rotation.
Exercises 18.1
-
What is meant by the term “conformation” in organic chemistry?
-
Why do alkanes exhibit different conformations?
-
What is torsional strain, and how does it affect alkane conformations?
-
What are the main differences between staggered and eclipsed conformations in ethane?
-
Why is the staggered conformation of ethane more stable than the eclipsed conformation?
-
How does steric hindrance influence the stability of different conformations in alkanes like butane and pentane?
-
Compare the energy profiles of ethane, propane, and butane. How does increasing chain length affect conformational energy differences?
-
Why is the gauche conformation of butane less stable than the anti conformation, despite both being staggered?
-
Explain how the concept of conformational analysis is important in understanding the behavior of cyclic alkanes like cyclohexane.
- In drug design, why is it important to consider the conformational preferences of alkyl chains within biologically active molecules?
Exercises 18.2: Conformational Analysis of Alkanes
Draw all Newman projections for a 3600 rotation around the C2-C3 bond of 2,3-Dimethylbutane.
Tips for drawing all the possible conformers about a certain C-C bond:
- View along that C-C bond; circle and decide what atoms/groups are connected on each carbon;
- Start with the staggered conformation in which the largest groups on each carbon are opposite (far away) to each other (this is the anti conformation);
- Keep the groups on one carbon “fixed”, and rotate the groups on the other carbon at 60° angles. Repeat the rotation five times, and you should get total of six conformers.
Exercises 18.3: Conformations of Alkanes
Draw the most and least stable conformations of 2,2,5-Trimethylhexane looking down C3-C4 bond.