1.3 – Populations and Samples

In order to understand the use of inferential statistics used in most research projects we need to understand the concept of research sampling.  As we discussed previously, many of our research questions can be about very large groups of people.  For example, we might want to know whether psychotherapy helps people with depression feel better.  This research question is focused on trying to determine if they typical psychotherapy can help all people who have depression.  However, it would be impossible to look at whether psychotherapy helps all depressed people feel better.  There are just too many people who are depressed to measure them all.

Instead, researchers would design a study to examine whether psychotherapy helps a small number of people with depression (perhaps 100) to feel better.  Essentially what the researchers are doing is sampling a small group of people from the large group of people that is the focus of the research question.

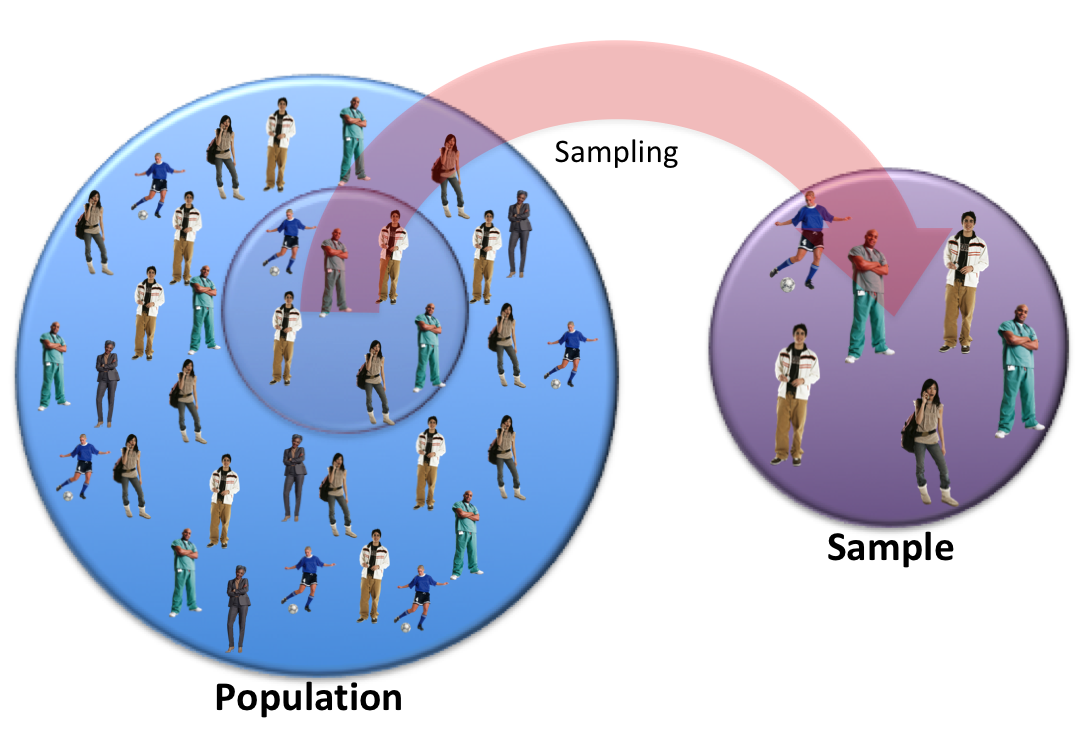
In research terminology, the population is the group of individuals that is the focus of the research question, while the sample is the subset of individuals selected from the population.

Populations can be any size; it all depends upon the research question.  With the research questions about psychotherapy helping people with depression, the population would be very large because it would need to include all depressed people, which would likely be in the millions.  However, if a researcher wanted to answer a research question about a specific classroom of 25 third-grade students, then the population would be the 25 third graders.

Likewise, samples can vary in size.  The size depends upon the size of the population as well as the decisions of the researcher.  With the third grade example, the sample cannot be any bigger than the population of 25 students.  Beyond that, it is then just a decision for the researcher.  How many third graders do they want to participate in the research?

With the psychotherapy example, the sample will be a subset of the millions of depressed people so it could be a very large sample, but the researcher is likely to use a much smaller group of individuals who are depressed because of the time and money involved in doing the research project.  So the sample could reasonably be somewhere around 30 to 1000 participants.

Because the sample is much easier and cheaper to work with, researchers will then do their research study on the sample, but then try to draw conclusions from the results and apply them to the population.  As you might guess, though, the quality of their conclusions depends a great deal upon the quality of the sample.  Specifically, it depends upon how well the sample represents the population.

When you look at the graphic above depicting a sample of 6 individuals selected from a population of 35 individuals, you can see that not all the types of people in the population have ended up in the sample.  And the sample seems to have a higher percentage of males than the population from which it was taken.  In other words, the sample might not be very representative of the population.  Thus, if the research results from the sample showed some interesting results, it might be problematic to conclude that the same results would happen with the population.

Now imagine instead that the researchers used a larger sample, say 25 people.  That sample is going to be much more representative of the population.  This is called the law of large numbers: larger samples tend to be more representative and thus are better for drawing inferences about the population.

The inferential statistics we will discuss later in the book will take these issues about sample size into account and will help researchers make decisions about how well the findings from a sample can apply to the population.