5.5 – Using Z-Scores to Translate to Other Scales

While we have just learned to use the z-score as a standardized score, sometimes we want to translate scores into a different standardized score. For example, we mentioned that all IQ tests scores are reported on a scale where the mean is μ = 100, and the standard deviation is σ = 15. How is that done?

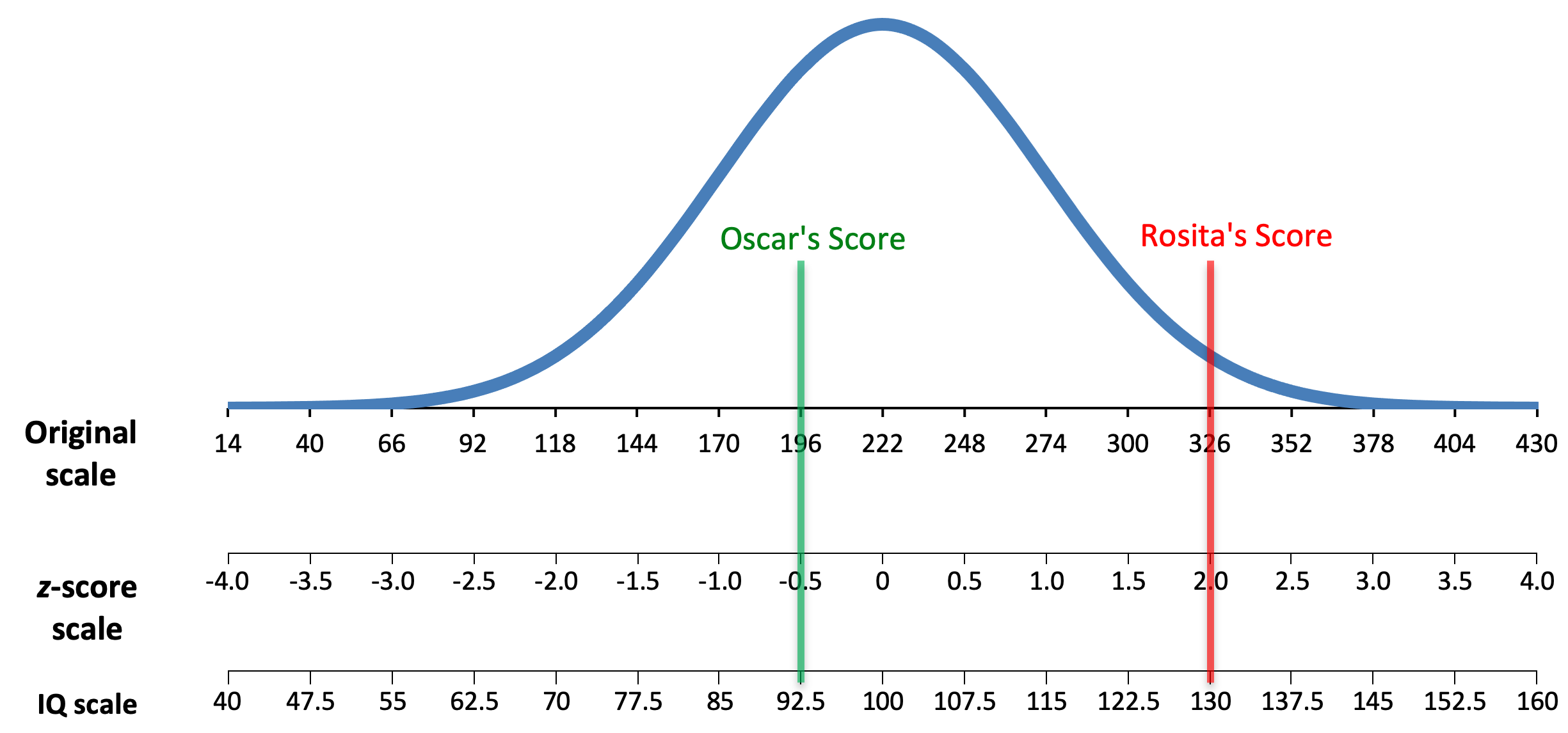
Suppose I create an IQ test and after giving it to a large number of people, I end up with an average score of μ = 222, and a standard deviation of σ = 52. In order to translate the scores to the appropriate standard scale (μ = 100, σ = 15), we need to follow two steps:

• Step 1: Calculate the z-score for each score, using:

[latex]z=\frac{X-\mu}{\sigma}[/latex]

• Step 2: Translate the z-score into the new scale, using:

[latex]X=\mu + z\sigma[/latex]

To demonstrate, let’s follow the process with just two possible scores on this test:

• Rosita earned a score of X = 326
• Oscar earned a score of X = 196

First, we calculate Rosita’s and Oscar’s z-scores using the formula that solves for z and then plug in the original mean and standard deviation:

[latex]\text{Rosita:   }z=\frac{X-\mu}{\sigma}=\frac{326-222}{52}=\frac{+104}{52}=+2.00[/latex]

[latex]\text{Oscar:   }z=\frac{X-\mu}{\sigma}=\frac{196-222}{52}=\frac{-26}{52}=-0.50[/latex]

We can see that Rosita scored 2 standard deviations above the mean, while Oscar scored half a standard deviation below the mean. Now, in step 2, we just need to translate those z-scores into the new scale where μ = 100 and σ = 15. To do that, we use the formula that solves for X and then plug in the new mean and standard deviation:

[latex]\text{Rosita:   }X = \mu + z\sigma=100+(+2.00)(15)=100+30=130[/latex]

[latex]\text{Oscar:   }X= \mu + z\sigma=100+(-0.50)(15)=100-7.5=92.5[/latex]

From this, we can see that Rosita’s IQ score on the new standardized scale is 130, while Oscar’s IQ score on the new standardized scale is 92.5. We have now successfully translated their original scores into the appropriate IQ scale.

If you look at the graph below, you can see that we haven’t changed where Rosita’s and Oscar’s scores fall relative to the other scores. We have simply just changed the scale.

If we were constructing this IQ test for use in psychological settings, we would then translate the appropriate IQ scale scores for every possible score on our test. Thankfully, we don’t need to do that. But now you know how to take any individual’s score from a given scale and translate the score onto a new scale.