SECTION 4.2: Data, Sampling, and Error

Most data is either categorical or quantitative.

Categorical Data is data that sorts the subjects into categories is called categorical (or qualitative) data. ye color is an example of a categorical variable with possible data values such as blue and brown. Often there will be only two categories of interest, such as the last example when yes and no were the possible data values.

Quantitative Data is data that describes a numerical aspect of a subject. Quantitative data can be further subdivided into data that represents a count, discrete data, and data that represents a measurement, continuous data. Data that represents a measurement can technically land anywhere on the number line, not necessarily on a whole number, even though we often round measurements to the nearest whole number.

If we wish to use sample data to infer characteristics of a population, the sample data must be representative of the population; it should have the same characteristics as the population. The way a researcher selects subjects from the population is called the sampling method.

The most ideal sampling method is a simple random sample, in which every set of n subjects has the same probability of being selected. This is like putting names in a hat and randomly selecting 5 names.

All of the inferential statistics methods we will study require that the data arise from a simple random sample, or SRS. The reason for this requirement is that if the data are not representative of the population, then the conclusions will be meaningless (GIGO: Garbage In, Garbage Out).

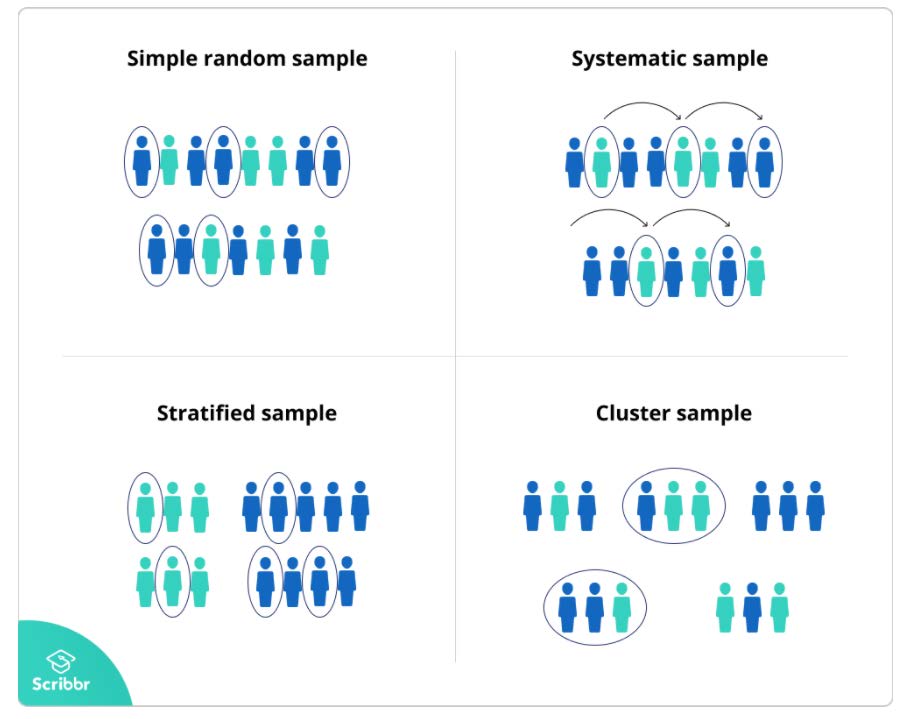
Often a simple random sample is not feasible, or at least not practical, so re-searchers will do their best to use other sampling methods that are likely to result in a representative sample. A few different sampling methods that may be used successfully are:

• Stratified Sampling: subjects are categorized by similar traits, then sample subjects are randomly selected from each category in numbers that are proportional to their numbers in the population.
  • Example: 4 girls are randomly selected and then 6 boys are randomly selected from a population that is 40% female. Stratified sampling guarantees a representative sample relative to the categories that are used.
• Cluster Sampling: there is already a natural categorization of subjects, usually by location. Sample of categories is selected randomly, and
  every subject in each of the selected categories is part of the sample.
  • Example: randomly select 10 elementary schools in Georgia, then sample every teacher at each of those schools. Cluster sampling is done for the sake of saving time and/or money.
• Systematic Sampling: sample every nth subject.
  • Example: sample every 1000th M&M to weigh and measure. Systematic sampling is common in manufacturing.

Sampling bias occurs when some members of the population are more likely to be chosen than others, resulting in a sample that is not representative of the population. The following sampling methods are common causes of sampling bias:

• Convenience Sample: collect data in a way that is convenient for the researcher, with little regard for obtaining a representative sample.
  • Example: a teacher sampling the students in her own classes to estimate the percentage of biology majors in the school.
• Voluntary Response/Self Selection: each subject actively chooses to participate.
  • Example: an Internet survey posted on a website.
  • Example: an observational study of the health benefits of drinking wheat grass juice.

It should be clear that there will always be natural variability in sampling. Two researchers could each select a sample of size 20 via a simple random sample from the same population, but they will end up with two different data sets; we would not expect the means of the two samples to
match, nor would we expect either sample mean to match the population mean exactly. This natural variability is called sampling error and it is a natural, unavoidable aspect of sampling and inferential statistics. We can, however, manage sampling error to a degree: larger sample sizes result in smaller sampling errors.

On the other hand, nonsampling error arises from factors that can and should be avoided. The following are examples of nonsampling errors that can arise in statistical studies:

• sampling bias: a natural, unavoidable aspect of sampling and inferential statistics
• self-interest study: sometimes the researcher or organization funding research has personal interest (usually monetary or political) in the outcome of a study. It is important to be aware of self-interest studies and carefully assess the statistical methods used in those cases.
  • Example: Dr. Andrew Wakefield’s research involving the MMR vaccine and autism.
• correlation/causality: if we identify a correlation between two variables, it is not necessarily the case that one causes the other.
  • Example: Ice cream causes drowning.
• non-response: a subject can always refuse to participate in a study, so this can become a problem if too many subjects refuse to participate.
  • Example: phone survey when everyone has caller id
• misleading use of data: incorrect graphs, incomplete data, or lack of context. Could be intentional or unintentional.
• undue influence/leading questions: asking questions in ways that lead the subject to a particular response.
  • Example: Do you agree with the administrations insightful decision regarding the name change?
• confounding: multiple factors could contribute to a particular outcome.
  • Example: when testing a particular diet, all subjects are required to exercise regularly.(Was it the diet or the exercise that caused the weight-loss?)