Section 2.4: The Pythagorean Theorem
Section 2.4 – The Pythagorean Theorem
A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles (triangles with a 90 degree angle). He discovered that the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.
The Pythagorean Theorem
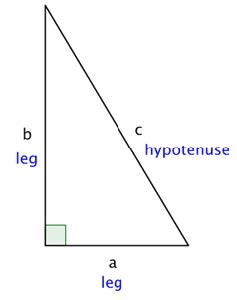
If a and b are the lengths of the legs of a right triangle and c is
the length of the hypotenuse, then the sum of the squares of
the lengths of the legs is equal to the square of the length of
the hypotenuse.
This relationship is represented by the formula:
𝑎2 + 𝑏2 = 𝑐2
leg2 + leg2 = hypotenuse2
Using the Theorem to Solve Real World Problems
The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real world settings. Architects and engineers use this formula when building ramps, bridges, and buildings. Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side.
