Section 2.7: Working in Three Dimensions: Volume

Section 2.7 – Working in Three Dimensions: Volume

In the world of geometry, it is common to see three-dimensional figures. In mathematics, a flat side of a three-dimensional figure is called a face. Polyhedrons are shapes that have four or more faces, each one being a polygon. These include cubes, prisms, and pyramids. Sometimes you may even see single figures that are composites of two of these figures. Let’s take a look at some common polyhedrons.

Identifying Solids

The first set of solids contains rectangular bases. Have a look at the table below, which shows each figure in both solid and transparent form.

Name Definition Solid Form Transparent Form
Cube A six-sided polyhedron that has
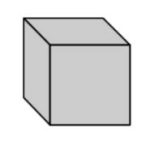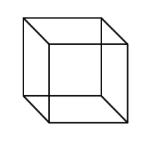congruent squares as faces.		 Solid form of a six-sided polyhedron that has congruent squares as faces. Transparent form of a six-sided polyhedron that has congruent squares as faces.
Rectangular Prism A polyhedron that has three pairs of
congruent, rectangular, parallel faces.		 Solid form of a polyhedron that has three pairs of congruent, rectangular, parallel faces. Transparent form of a polyhedron that has three pairs of congruent, rectangular, parallel faces.
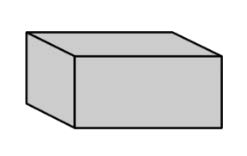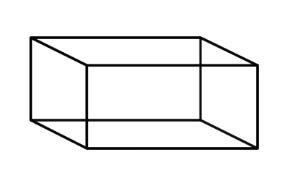Pyramid A polyhedron with a polygonal base
and a collection of triangular faces that
meet at a point.		 Solid form of a polyhedron with a polygonal base and a collection of triangular faces that meet at a point. Transparent form of a polyhedron with a polygonal base and a collection of triangular faces that meet at a point.
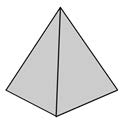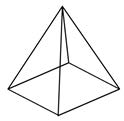Cylinder A solid figure with a pair of circular,
parallel bases and a round, smooth face
between them.		 Solid form of a solid figure with a pair of circular, parallel bases and a round, smooth face between them. Transparent form of a solid figure with a pair of circular, parallel bases and a round, smooth face between them.
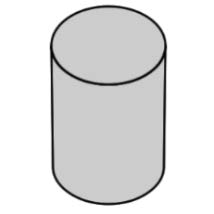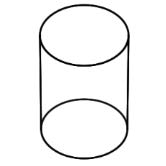Cone A solid figure with a single circular
base and a round, smooth face that
diminishes to a single point.		 Solid form of a solid figure with a single circular base and a round, smooth face that diminishes to a single point. Transparent form of a solid figure with a single circular base and a round, smooth face that diminishes to a single point.
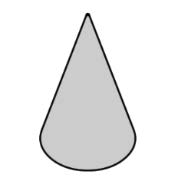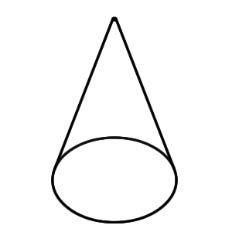Sphere A solid, round figure where every point
on the surface is the same distance from
the center.		 Solid form of a solid, round figure where every point on the surface is the same distance from the center. Transparent form of a solid, round figure where every point on the surface is the same distance from the center.

Volume

Recall that perimeter measures one dimension (length), and area measures two dimensions (length and width). To measure the amount of space a three-dimensional figure takes up, you use another measurement called volume.

Volume is measured in cubic units. A shoebox may be measured in cubic inches (usually represented as in3 or inches3), while the Great Pyramid of Egypt would be more appropriately measured in cubic meters (m3 or meters3).

Name Transparent Form Volume Formula
Cube 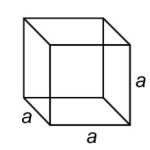Solid form of a six-sided polyhedron that has congruent squares as faces, with each side labeled with length a.

V = a · a · a = a3 

a = the length of one side
Rectangular Prism 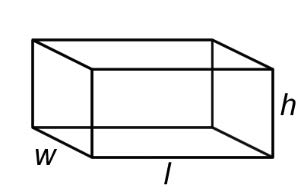Solid form of a polyhedron that has three pairs of congruent, rectangular, parallel faces, with side length of l, width by w, and height of h.

V = l · w · h

l = length
w = width
h = height
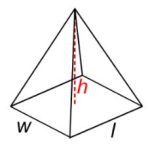Pyramid Solid form of a polyhedron with a polygonal base and a collection of triangular faces that meet at a point, with side length of l, width by w, and height of h.

V = [latex]\frac{l{\cdot}w{\cdot}h}{3}[/latex]

l = length
w = width
h = height
Cylinder 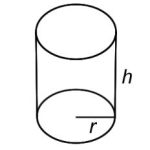Solid form of a solid figure with a pair of circular, parallel bases with a radius of r, and a round, smooth face between them, with a height of h.

V = 𝝅𝒓𝟐𝒉

r = width
h = height
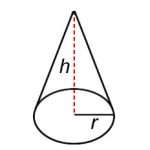Cone Solid form of a solid figure with a single circular base with a radius of r and a round, smooth face that diminishes to a single point, with a height of h.

 

V = [latex]\frac{{\pi}r^2~h}{3}[/latex]

r = width
h = height
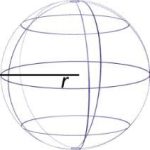Sphere Solid form of a solid, round figure where every point on the surface is the same distance from the center with radius r.

V = [latex]\frac{4}{3}[/latex]𝝅𝒓3

r = radius

Content from text: College Mathematics, Second Edition

creative commons by no changes share alike

College Mathematics by Scottsdale Community College is licensed under a

Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Unported License.

License

MAT112 Mathematical Concepts & Applications Copyright © by Leah Polanski. All Rights Reserved.

Share This Book