Section 2.5: Circles
Section 2.5 – Circles
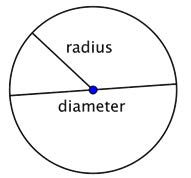
A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle to any point on the circle is called the radius. When two radii (the plural of radius) are put together to form a line segment across the circle, you have a diameter. The diameter of a circle passes through the center of the circle and has its endpoints on the circle itself. The diameter of any circle is two times the length of that circle’s radius. It can be represented by the expression 2r, or “two times the radius.”
Circumference of a Circle
To find the circumference (C) of a circle, use one of the following formulas:
If you know the diameter (d) of a circle: C = πd
If you know the radius (r) of a circle: C = 2πr
The distance around a circle is called the circumference. (Recall, the distance around a polygon is the perimeter.) One interesting property about circles is that the ratio of a circle’s circumference and its diameter is the same for all circles. No matter the size of the circle, the ratio of the circumference and diameter will be the same.
Area of a Circle
To find the area (A) of a circle, use the formula: A = πr2
Where r is the radius of the circle.
Pi -- π
Pi is a non-terminating, non-repeating decimal, so it is impossible to write it out completely. The first 10 digits of π are 3.141592653; it is often rounded to 3.14 or estimated as the fraction [latex]\frac{22}{7}[/latex] . Note that both 3.14 and [latex]\frac{22}{7}[/latex] are approximations of π, and are used in calculations where it is not important to be precise.
