Sections 2.1 – 2.7: Geometry

Section 2.1 – Geometry Basics

A point is simply a location, which has no dimensions! That might seem strange, but the geometric idea of a point is that it has no length, no width, and no height.

Any two distinct points, we now can form a line connecting the two points. A line is a one-dimensional figure (it has length, but no width and no height) that is made up of an infinite number of individual points placed side by side. In geometry all lines are assumed to be straight; if they bend they are called a curve. A line continues infinitely (forever) in two directions, usually indicated by placing arrows at the two ends.

A line segment does not continue infinitely in two directions, but has two endpoints, usually indicated by placing points at the two ends.

A plane is a flat surface that continues forever (or, in mathematical terms, infinitely) in every direction. It has two dimensions: length and width. You can visualize a plane by placing a piece of paper on a table. Now imagine that the piece of paper stays perfectly flat and extends as far as you can see in four directions, left-to-right and front-to-back.

Section 2.2 – Perimeter

The perimeter of a two-dimensional shape is the distance around the shape. You can think of wrapping a string around the 3 sides of a triangle. The length of this string would be the perimeter of the triangle. Or walking around the outside of a park, you walk the distance of the park’s perimeter. Some people find it useful to think “peRIMeter” because the edge of an object is its rim and peRIMeter has the word “rim” in it.

If the shape is a polygon–a closed, two-dimensional shape with straight sides– then you can add up all the lengths of the sides to find the perimeter. Be careful to make sure that all the lengths are measured in the same units. You measure perimeter in linear units, which is one dimensional. Examples of units of measure for length are inches, centimeters, or feet.

Section 2.3 – Area

The area of a two-dimensional figure describes the amount of surface the shape covers. You measure area in square units of a fixed size. Examples of square units of measure are square inches, square centimeters, or square miles. When finding the area of a polygon, you count how many squares of a certain size will cover the region inside the polygon.

The formulas you are going to look at are all developed from the understanding that you are counting the number of square units inside the polygon.

Shape	Area
Rectangle with side lengths a, b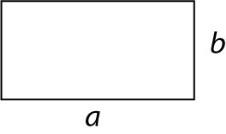	𝐴 = a ∙ b
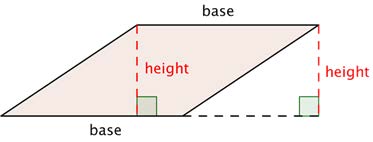
Parallelogram with height h and base b	𝐴 = 𝑏 ∙ ℎ
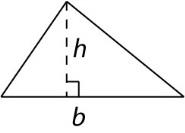
Triangle with height h and base b	𝐴 = [latex]\frac{1}{2}[/latex]𝑏ℎ
Trapezoid as shown below:	𝐴 = [latex]\frac{b_1~+~b_2}{2}[/latex]ℎ

Section 2.4 – The Pythagorean Theorem

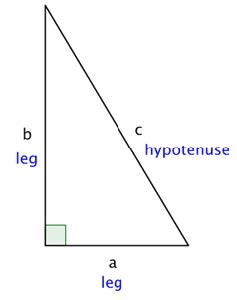
A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles (triangles with a 90 degree angle). He discovered that the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.

The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real world settings. Architects and engineers use this formula when building ramps, bridges, and buildings. Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side.

Section 2.5 – Circles

A circle represents a set of points, all of which are the same distance away from a fixed, middle point. This fixed point is called the center. The distance from the center of the circle to any point on the circle is called the radius. When two radii (the plural of radius) are put together to form a line segment across the circle, you have a diameter. The diameter of a circle passes through the center of the circle and has its endpoints on the circle itself. The diameter of any circle is two times the length of that circle’s radius. It can be represented by the expression 2r, or “two times the radius.”

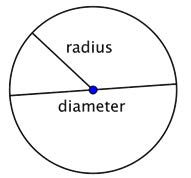
The distance around a circle is called the circumference. (Recall, the distance around a polygon is the perimeter.) One interesting property about circles is that the ratio of a circle’s circumference and its diameter is the same for all circles. No matter the size of the circle, the ratio of the circumference and diameter will be the same.

Pi is a non-terminating, non-repeating decimal, so it is impossible to write it out completely. The first 10 digits of π are 3.141592653; it is often rounded to 3.14 or estimated as the fraction [latex]\frac{22}{7}[/latex] . Note that both 3.14 and [latex]\frac{22}{7}[/latex] are approximations of π, and are used in calculations where it is not important to be precise.

Section 2.6 – Perimeter and Area of Composite Figures

Often you need to find the area or perimeter of a shape that is not a standard polygon. Artists and architects, for example, usually deal with complex shapes. However, even complex shapes can be thought of as being composed of smaller, less complicated shapes, like rectangles, trapezoids, and triangles.

You need to create regions within the shape for which you can find the area, and add these areas together. The trick to figuring out these types of problems is to identify shapes (and parts of shapes) within the composite figure, calculate their individual dimensions and then add them together.

Section 2.7 – Working in Three Dimensions: Volume

In the world of geometry, it is common to see three-dimensional figures. In mathematics, a flat side of a three-dimensional figure is called a face. Polyhedrons are shapes that have four or more faces, each one being a polygon. These include cubes, prisms, and pyramids. Sometimes you may even see single figures that are composites of two of these figures. Let’s take a look at some common polyhedrons.

The first set of solids contains rectangular bases. Have a look at the table below, which shows each figure in both solid and transparent form.

Name	Definition	Solid Form	Transparent Form
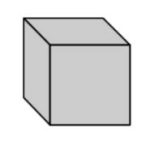
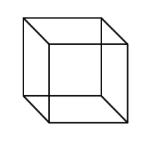
Cube	A six-sided polyhedron that has congruent squares as faces.
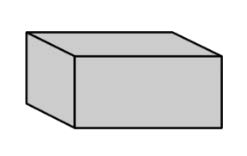
Rectangular Prism	A polyhedron that has three pairs of congruent, rectangular, parallel faces.
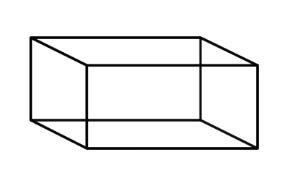Pyramid	A polyhedron with a polygonal base and a collection of triangular faces that meet at a point.
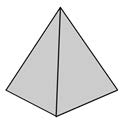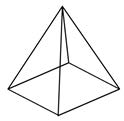Cylinder	A solid figure with a pair of circular, parallel bases and a round, smooth face between them.
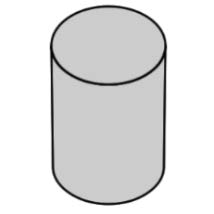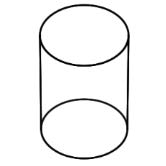Cone	A solid figure with a single circular base and a round, smooth face that diminishes to a single point.
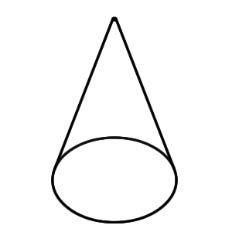Sphere	A solid, round figure where every point on the surface is the same distance from the center.

Recall that perimeter measures one dimension (length), and area measures two dimensions (length and width). To measure the amount of space a three-dimensional figure takes up, you use another measurement called volume.

Volume is measured in cubic units. A shoebox may be measured in cubic inches (usually represented as in³ or inches³), while the Great Pyramid of Egypt would be more appropriately measured in cubic meters (m³ or meters³).

Name	Transparent Form	Volume Formula
Cube		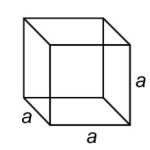V = a · a · a = a3  a = the length of one side
Rectangular Prism		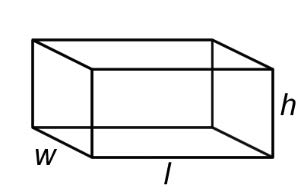V = l · w · h l = length w = width h = height
Pyramid		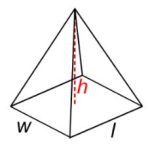V = [latex]\frac{l{\cdot}w{\cdot}h}{3}[/latex] l = length w = width h = height
Cylinder		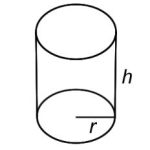V = 𝝅𝒓𝟐𝒉 r = width h = height
Cone		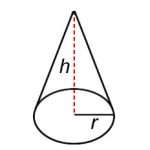V = [latex]\frac{{\pi}r^2~h}{3}[/latex] r = width h = height
Sphere		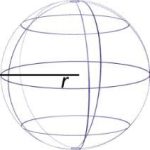V = [latex]\frac{4}{3}[/latex]𝝅𝒓3 r = radius

Content from text: College Mathematics, Second Edition

College Mathematics by Scottsdale Community College is licensed under a

Creative Commons Attribution-NonCommercial-ShareAlike 4.0 Unported License.