2. Conservative and Non-Conservative Forces

In Potential Energy and Conservation of Energy, any transition between kinetic and potential energy conserved the total energy of the system. This was path independent, meaning that we can start and stop at any two points in the problem, and the total energy of the system—kinetic plus potential—at these points are equal to each other. This is characteristic of a conservative force. We dealt with conservative forces in the preceding section, such as the gravitational force and spring force. When comparing the motion of the football in (Figure), the total energy of the system never changes, even though the gravitational potential energy of the football increases, as the ball rises relative to ground and falls back to the initial gravitational potential energy when the football player catches the ball. Non-conservative forces are dissipative forces such as friction or air resistance. These forces take energy away from the system as the system progresses, energy that you can’t get back. These forces are path dependent; therefore it matters where the object starts and stops.

[In (Figure), we use the notation of a circle in the middle of the integral sign for a line integral over a closed path, a notation found in most physics and engineering texts.] (Figure) and (Figure) are equivalent because any closed path is the sum of two paths: the first going from A to B, and the second going from B to A. The work done going along a path from B to A is the negative of the work done going along the same path from A to B, where A and B are any two points on the closed path:

You might ask how we go about proving whether or not a force is conservative, since the definitions involve any and all paths from A to B, or any and all closed paths, but to do the integral for the work, you have to choose a particular path. One answer is that the work done is independent of path if the infinitesimal work [latex]\stackrel{\to }{F}·d\stackrel{\to }{r}[/latex] is an exact differential, the way the infinitesimal net work was equal to the exact differential of the kinetic energy, [latex]d{W}_{\text{net}}=m\stackrel{\to }{v}·d\stackrel{\to }{v}=d\frac{1}{2}m{\text{v}}^{2},[/latex]

when we derived the work-energy theorem in Work- Kinetic Energy Theorem. There are mathematical conditions that you can use to test whether the infinitesimal work done by a force is an exact differential, and the force is conservative. These conditions only involve partial differentiation and are thus relatively easy to apply.

Calculus Interlude 

At this point, you may think of an ordinary derivative as only a slope.  While this graphical interpretation of a derivative is certainly important, an ordinary derivative has a more general meaning.  The mathematical operation [latex]\frac{dF}{dx}[/latex] tells us how the single variable function F changes when the parameter x is varied slightly.  Consider the area of a circle, which is a function of a single variable, with that variable being the radius of the circle:

[latex]A = \pi r^2[/latex]

Now, the radius is something you would measure (in actuality, you would likely measure the diameter and then calculate the radius) in order to be able to determine the area of the circle.  All measurements have some uncertainty, so what if the actual radius of the circle were slightly larger than the measured radius? The new radius, [latex]r + \Delta r[/latex] means that the area of the circle, [latex]A[/latex] is off by an amount [latex]\Delta A[/latex]:

Cutting the dark blue annular ring and rolling it out, we can determine the area of that dark blue shaded region:

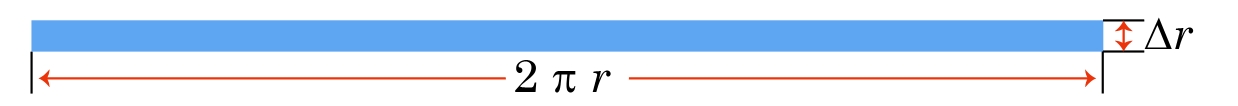
[latex]\Delta A = (2 \pi r) (\Delta r)[/latex]

or

[latex]\frac{\Delta A}{\Delta r} = 2 \pi r[/latex]

Notice what the derivative of the area function with respect to the radius of the circle gives:

[latex]\frac{dA}{dr} = \frac{d}{dr}(\pi r^2) = 2 \pi r[/latex]

Or, [latex]\frac{\Delta A}{\Delta r}[/latex] and [latex]\frac {dA}{dr}[/latex] give exactly the same result: the rate at which the area changes with respect to a small change in the radius of the circle (remember that [latex]dr[/latex] is infinitesimally small).

Multivariable Functions and Partial Derivatives

In many situations in science and engineering, functions depend on more than one parameter (or variable).  For multivariable functions, an ordinary derivative doesn’t have a lot of meaning.  The volume of a right circular cylinder, for example depends on two parameters: the radius of the cylinder, [latex]r[/latex], and the height of the cylinder, [latex]h[/latex]:

[latex]V = \pi r^2 h[/latex]

In order to evaluate [latex]\frac {dV}{dr}[/latex] or [latex]\frac{dV}{dh}[/latex], one must use implicit differentiation and then a mathematical relationship between [latex]r[/latex] and [latex]h[/latex] must somehow be determined in order to evaluate the [latex]\frac{dh}{dr}[/latex] and [latex]\frac{dr}{dh}[/latex] that appear during the implicit differentiation process. Fortunately, there is a mathematical process that allows for the rate at which a multivariable function changes with a small variation in only one of the parameters, with all other parameters held constant. This is called a partial derivative. A partial derivative is indicated in a manner similar to that of an ordinary derivative, except that a partial derivative is indicated using [latex]\partial[/latex] (a lower-case, Greek letter “del”) rather than a lower-case d in the differentiation operator. For example, the partial derivative of the volume of the cylinder with respect to its height would be written [latex]\frac{\partial V}{\partial h}[/latex] and would represent the rate at which the volume of the cylinder changes with a small variation in height while the radius of the cylinder is held constant. The figure below shows a cylinder of radius, [latex]r[/latex], and height, [latex]h[/latex]. The height of the cylinder is varied by an amount, [latex]\Delta h[/latex], while the radius is held constant. This results in an additional volume, [latex]\Delta V[/latex], shown in dark blue:

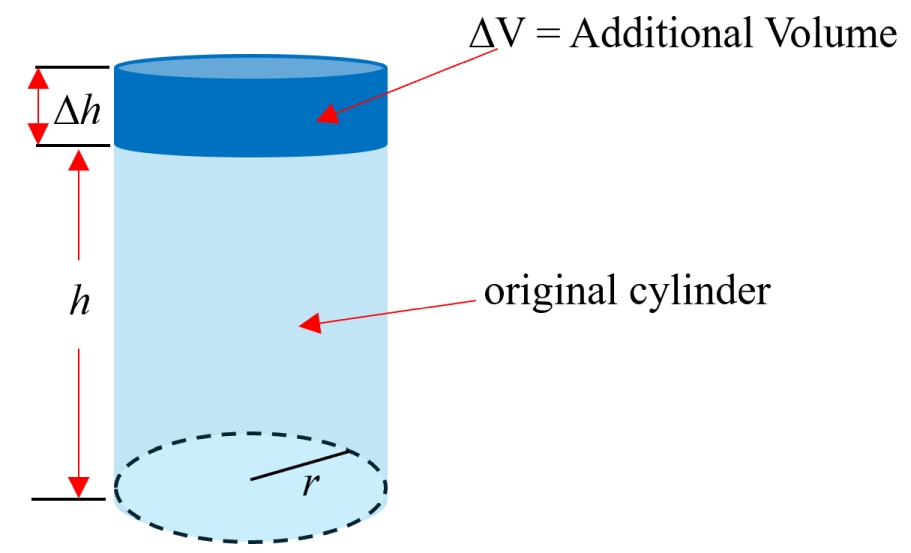
The additional volume, [latex]\Delta V[/latex], is then the volume of the dark blue cylinder:

[latex]\Delta V = \pi r^2 \Delta h[/latex]

Or,

[latex]\frac{\Delta V}{\Delta h} = \pi r^2[/latex]

Next, we evaluate [latex]\frac{\partial V}{\partial h}[/latex]. Remember, that in evaluating a partial derivative any parameter that is not the parameter with respect to which you are differentiating is treated as a constant. In this case, that means the radius of the base of the cylinder, [latex]r[/latex] is treated like a constant:

[latex]\frac{\partial V}{\partial h} = \frac{\partial}{\partial h}(\pi r^2 h) = \pi r^2 [\frac{\partial}{\partial h}(h)] = \pi r^2 \frac{\partial h}{\partial h}= \pi r^2[/latex]

Since [latex]\frac{\Delta V}{\Delta h}[/latex] and [latex]\frac{\partial V}{\partial h}[/latex] give the same result, we can conclude that [latex]\frac{\partial V}{\partial h}[/latex] gives the rate at which the volume of the cylinder changes when one, and only one, of the determining parameters is varied, in this case the height of the cylinder.

In two dimensions, the condition for [latex]\stackrel{\to }{F}·d\stackrel{\to }{r}={F}_{x}dx+{F}_{y}dy[/latex] to be an exact differential is

You may recall that the work done by the force in (Figure) depended on the path. For that force,

Therefore,

which indicates it is a non-conservative force. Can you see what you could change to make it a conservative force?

Before leaving this section, we note that non-conservative forces do not have potential energy associated with them because the energy is lost to the system and can’t be turned into useful work later. So there is always a conservative force associated with every potential energy. We have seen that potential energy is defined in relation to the work done by conservative forces. That relation, (Figure), involved an integral for the work; starting with the force and displacement, you integrated to get the work and the change in potential energy. However, integration is the inverse operation of differentiation; you could equally well have started with the potential energy and taken its derivative, with respect to displacement, to get the force. The infinitesimal increment of potential energy is the dot product of the force and the infinitesimal displacement,

Here, we chose to represent the displacement in an arbitrary direction by [latex]d\stackrel{\to }{l},[/latex] so as not to be restricted to any particular coordinate direction. We also expressed the dot product in terms of the magnitude of the infinitesimal displacement and the component of the force in its direction. Both these quantities are scalars, so you can divide by dl to get

This equation gives the relation between force and the potential energy associated with it. In words, the component of a conservative force, in a particular direction, equals the negative of the derivative of the corresponding potential energy, with respect to a displacement in that direction. For one-dimensional motion, say along the x-axis, (Figure) give the entire vector force, [latex]\stackrel{–}{F}={F}_{x}\hat{i}=-\frac{\partial U}{\partial x}\hat{i}.[/latex]

In two dimensions,

From this equation, you can see why (Figure) is the condition for the work to be an exact differential, in terms of the derivatives of the components of the force. In general, a partial derivative notation is used. If a function has many variables in it, the derivative is taken only of the variable the partial derivative specifies. The other variables are held constant. In three dimensions, you add another term for the z-component, and the result is that the force is the negative of the gradient of the potential energy. However, we won’t be looking at three-dimensional examples just yet.