Solve Proportions

A proportion is a statement that shows that two ratios are equal, in other words, it is an equation of two ratios. To calculate dosages, the nurse needs to use the ratio and proportion. Like a ratio, a proportion can be written using a linear format, for example: 1:2::2:4 or 5 mg: 1 tablet :: 10 mg: 2 tablets.

Learning Objectives

By the end of this section, students will be able to:

Use the Definition of Proportion:

When two ratios or rates are equal, the equation relating them is called a proportion.

Proportion

A proportion is an equation of the form \( \frac{a}{b} = \frac{c}{d} \), where \( b \neq 0, \, d \neq 0 \).

The proportion states two ratios or rates are equal. The proportion is read as “𝑎 is to 𝑏, as 𝑐 is to 𝑑”.

The equation \( \frac{1}{2} = \frac{4}{8} \) is a proportion because the two fractions are equal. The proportion \( \frac{1}{2} = \frac{4}{8} \) is read “1 is to 2 as 4 is to 8”.

If we compare quantities with units, we have to be sure we are comparing them in the right order. For example, in the proportion \frac{20 \text{ students}}{1 \text{ teacher}} = \frac{60 \text{ students}}{3 \text{ teachers}} we compare the number of students to the number of teachers. We put students in the numerators and teachers in the denominators.

Example 6.40

Write each sentence as a proportion:

  1. ⓐ 3 is to 7 as 15 is to 35.
  2. ⓑ 5 hits in 8 tries is the same as 30 hits in 48 tries.
  3. ⓒ $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces.

Solution:

ⓐ Start with the comparison. 3 is to 7 as 15 is to 35.
Write as a proportion. \frac{3}{7}=\frac{15}{35}
ⓑ Start with the comparison. 5 hits in 8 tries is the same as 30 hits in 48 tries.
Write each fraction to compare hits to tries. \frac{\text{hits}}{\text{tries}} = \frac{\text{hits}}{\text{tries}}
Write as a proportion. \frac{3}{7}=\frac{15}{35}
ⓒ Start with the comparison. $1.50 for 6 ounces is equivalent to $2.25 for 9 ounces.
Write each fraction to compare dollars to ounces. \frac{\text{\$}}{\text{ounces }} = \frac{\text{\$}}{\text{ounces }}
Write as a proportion. \frac{1.50}{6}=\frac{2.25}{9}

Try It: Write each sentence as a proportion.

Look at the proportions \(\frac{1}{2}=\frac{4}{8} \)  and \(\frac{2}{3}=\frac{6}{9} \). From our work with equivalent fractions, we know these equations are true. But how do we know if an equation is a proportion with equivalent fractions if it contains fractions with larger numbers?

To determine if a proportion is true, we find the cross products of each proportion. To find the cross products, we multiply each denominator with the opposite numerator (diagonally across the equal sign). The results are called a cross product because of the cross formed. If, and only if, the given proportion is true, that is, the two sides are equal, then the cross products of a proportion will be equal.

The figure shows cross multiplication of two proportions. There is the proportion 1 is to 2 as 4 is to 8. Arrows are shown diagonally across the equal sign to show cross products. The equations formed by cross multiplying are 8 · 1 = 8 and 2 · 4 = 8. There is the proportion 2 is to 3 as 6 is to 9. Arrows are shown diagonally across the equal sign to show cross products. The equations formed by cross multiplying are 9 · 2 = 18 and 3 · 6 = 18.

Cross Products of a Proportion

For any proportion of the form \( \frac{a}{b} = \frac{c}{d} \), where \( b \neq 0, \, d \neq 0 \), its cross products are equal.

Mathematical equation with fractions showing cross-multiplication. At the top, the equation "a · d = b · c" is shown. Below it, there is a diagram showing two equal fractions: "a/b" equals "c/d". A light blue arrow points diagonally across the equals sign from b in the left denominator to c in the right numerator> Another light blue arrow points diagonally across the equals sign from d in the right denominator to a in the left numerator. The two arrows form an "X" shape across the equation. The arrows indicate the cross-multiplication between the terms of the fractions.

Cross products can be used to test whether a proportion is true. To test whether an equation makes a proportion, we find the cross products. If they are both equal, we have a proportion.

Example 6.41

Determine whether each equation is a proportion:

  1. ⓐ \(\frac{4}{9}=\frac{12}{28} \)
  2. ⓑ \(\frac{17.5}{37.5}=\frac{7}{15} \)

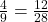
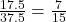
Solution

ⓐ

 Start with the given equation. \frac{4}{9}=\frac{12}{28}
Find the cross products. \( 28 \cdot 4 = 112 \)  |  \( 28 \cdot 4 = 112 \)

Since the cross products are not equal, \( 28 \cdot 4 \neq 9 \cdot 12 \), the equation is not a proportion.

ⓑ

Start with the given equation. \(\frac{17.5}{37.5}=\frac{7}{15} \)
Find the cross products. \( 15 \cdot 17.5 = 262.5 \)  |  \( 37.5 \cdot 7 = 262.5 \)

Since the cross products are equal, \( 15 \cdot 17.5 = 37.5 \cdot 7 \), the equation is a proportion.

 Try It: Determine whether each equation is a proportion.

Solve Proportions

To solve a proportion containing a variable, remember that the proportion is an equation. All of the techniques we have used so far to solve equations still apply. In the next example, we will solve a proportion by multiplying by the Least Common Denominator (LCD) using the Multiplication Property of Equality.

Example 6.42

Solve: \( \frac{x}{63} = \frac{4}{7} \).

Solution:

Start with the given proportion. \( \frac{x}{63} = \frac{4}{7} \)
To isolate \(x\), multiply both sides by the LCD, \(63\). 63 (\frac{x}{63})=63 (\frac{4}{7})
Divide the common factors. x=\frac{9 \cdot \cancel 7 \cdot 4}{\cancel 7}
Simplify. x=36

So our solution is: \(x=36 \). But we need to check our answer.

To check our answer, rewrite the original proportion. \( \frac{x}{63} = \frac{4}{7} \)
Substitute our answer, \(36\), for  \(x\). \frac{36}{63} \overset{?}{=} \frac{4}{7}
Show and cancel out common factors in the numerator and denominator. \frac{4 \cdot \cancel{9}}{7 \cdot \cancel{9}} \overset{?}{=} \frac{4}{7}
Simplify. \frac{4}{7} = \frac{4}{7} \checkmark

Our check confirms that our solution is correct.

Try It: Solve proportions.

When the variable is in a denominator, we’ll use the fact that the cross products of a proportion are equal to solve the proportions:

  1. First, we find the cross products of the proportion
  2. Then we set them equal.
  3. Then we solve the resulting equation using our familiar techniques.

Example 6.43

Solve: \( \frac{144}{a} = \frac{9}{4} \).

Solution:

Notice that the variable is in the denominator, so we will solve by finding the cross products and setting them equal.

Start with the given proportion. \frac{144}{a} = \frac{9}{4}
Find the cross products and set them equal. 4 \cdot 144=a \cdot 9
Simplify 576=9a
To isolate \(x\), divide both sides by \(9\). \frac{576}{9} = \frac{9a}{9}
Simplify. 64=a

So our solution is: \(a=64 \). Check our answer by substituting the solution in the original equation.

To check our answer, rewrite the original proportion. \frac{144}{a} = \frac{9}{4}
Substitute our answer, \(64\), for  \(a\).  \frac{144}{64} \overset{?}{=} \frac{9}{4}
Show and cancel out common factors in the numerator and denominator. \frac{9 \cdot \cancel{16}}{4 \cdot \cancel{16}} \overset{?}{=} \frac{9}{4}
Simplify. \frac{9}{4} = \frac{9}{4} \checkmark

Our check confirms that our solution is correct.

Another method to solve this would be to multiply both sides by the LCD, \( 4a \). Try it and verify that you get the same solution.

Try It: Solve proportions.

Example 6.44

Solve: \( \frac{52}{91} = \frac{-4}{y} \).

Solution:

Start with the given proportion. \frac{52}{91} = \frac{-4}{y}
Find the cross products and set them equal. 52 \cdot y=91(-4)
Simplify 52y=-364
To isolate \(x\), divide both sides by \(52\). \frac{52y}{52} = \frac{-364}{52}
Simplify. [latexy=-7[/latex]

So our solution is: \(y=-7 \). Check our answer by substituting the solution in the original equation.

To check our answer, rewrite the original proportion. \frac{52}{91} = \frac{-4}{y}
Substitute \(-7\) for  \(y\). \frac{52}{91} \overset{?}{=} \frac{-4}{-7}
Show and cancel out common factors. \frac{4 \cdot \cancel{13}}{7 \cdot \cancel{13}} \overset{?}{=} \frac{\cancel{-}4}{\cancel{-}7}
Simplify. \frac{4}{7} = \frac{4}{7} \checkmark

Our check confirms that our solution is correct.

Try It: Solve proportions. 

Solve Applications Using Proportions

Since proportions are equations, we can use this fact as a strategy for solving for an unknown variable in a proportion. When we set up the proportion, we must make sure the units are correct—the units in the numerators match and the units in the denominators match.

Example 6.45

When pediatricians prescribe acetaminophen to children, they prescribe 5 milliliters (ml) of acetaminophen for every
25 pounds of the child’s weight. If Zoe weighs 80 pounds, how many milliliters of acetaminophen will her doctor prescribe?

Solution:

Identify what you are asked to find. How many mL of acetaminophen the doctor will prescribe
Choose a variable to represent it. Let \( a=mL \) of acetaminophen.
Write a sentence that gives the information to find it. If 5 mL is prescribed for every 25 pounds, how much will be prescribed for 80 pounds?
Translate into a proportion. \frac{mL}{pounds}=\frac{mL}{pounds}
Substitute given values—be careful of the units. \frac{5}{25}=\frac{a}{80}
To isolate

    \[\(a\)\]

, multiply both sides by

    \[\(80\)\]

 80 \cdot \frac{5}{25}=80 \cdot \frac{a}{80}
Show and cancel out common factors. \frac{16 \cdot \cancel{5}\cdot \cancel{5}}{\cancel{5}\cdot \cancel{5}}= \frac{\cancel{80}a}{\cancel{80}}
Simplify. 16 = a
Check if the answer is reasonable. Yes. Since 80 is about 3 times 25, the medicine should be about 3 times 5.
Write the answer as a complete sentence. The pediatrician would prescribe 16 mL of acetaminophen to Zoe.

You could also solve this proportion by setting the cross products equal. Try it to confirm you get the same answer.

Try It: Solve applications using proportions. 

Example 6.46

One brand of microwave popcorn has 120 calories per serving. A whole bag of this popcorn has 3.5
servings. How many calories are in a whole bag of this microwave popcorn?

Solution:

Identify what you are asked to find. How many calories are in a whole bag of microwave popcorn?
Choose a variable to represent it. Let \( c= \) number of calories.
Write a sentence that gives the information to find it. If there are 120 calories per serving, how many calories are in a whole bag with 3.5 servings?
Translate into a proportion. \frac{calories}{serving}=\frac{calories}{serving}
Substitute given values. \frac{120}{1}=\frac{c}{3.5}
Multiply both sides by

    \[\(3.5\)\]

 (3.5)(\frac{120}{1})=(3.5)(\frac{c}{3.5})
Calculate. 420=c}
Check if the answer is reasonable. Yes. Since 3.5 is between 3 and 4, the total calories should be between 360 (3⋅120) and 480 (4⋅120).
Write the answer as a complete sentence. The whole bag of microwave popcorn has 420 calories.

 

Try It: Solve applications using proportions. 

Example 6.47

Josiah went to Mexico for spring break and changed $325 dollars into Mexican pesos. At that time, the exchange rate had $1 U.S. as equal to 12.54 Mexican pesos. How many Mexican pesos did he get for his trip?

Solution:

Identify what you are asked to find. How many Mexican pesos did Josiah get?
Choose a variable to represent it. Let \( p= \) number of pesos.
Write a sentence that gives the information to find it. If $1 U.S. is equal to 12.54 Mexican pesos, then $325 is how many pesos?
Translate into a proportion. \frac{dollars}{pesos}=\frac{dollars}{pesos}
Substitute given values. \frac{1}{12.54}=\frac{325}{p}
The variable is in the denominator, so find the cross products and set them equal. p \cdot 1=12.54(325)
Simplify and calculate. c=4075.5
Check if the answer is reasonable. Yes, $100 would be 1,254 pesos. $325 is a little more than 3 times this amount.
Write the answer as a complete sentence. Josiah has 4075.5 pesos for his spring break trip.

 

Try It: Solve applications using proportions.

Practice Makes Perfect

Use the Definition of a Proportion

Practice writing sentences as a proportion.

Practice determining whether an equation is a proportion.

Solve Proportions

Practice solving proportions.

Practice solving proportion problems.

Self Check

After completing the exercises, use this table to evaluate your mastery of the objectives of this section. For each skill listed in a table row, rate yourself in the column that best describes your confidence level.

Solve Proportions Self-Check
I can … Confidently With some help No – I don’t get it!
use the definition of proportion.
solve proportions.
solve applications using proportions.

If most of your checks were:

  • …confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident in your ability to do these things? Be specific.
  • …with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, and in nursing, every topic builds upon previous work. It is important to ensure you have a strong foundation before you move on. Who can you ask for help? Is there a place on campus where math tutors are available? Can your study skills be improved?
  • …no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor, student success specialist, or math tutor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Chapter Attributions

This chapter was adapted by Corinn Herrell and Cheryl Colan from “6.5 Solve Proportions and their Applications” in Prealgebra 2e by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis. Licensed under a CC BY 4.0 license.

License

Icon for the Creative Commons Attribution 4.0 International License

College Mathematics Review for Nursing Students Copyright © 2024 by Phoenix College Nursing is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book