Dimensional Analysis

Corinn Herrell; Cheryl Colan; Fatima Baig

Dimensional Analysis

Dimensional analysis is a method used by nurses to calculate dosages. It allows the nurse to set up one equation to solve the problem, even if multiple unit conversions are required.

Learning Objectives

By the end of this section, students will be able to:

Use dimensional analysis to convert between different units of measurement for height/length, weight/mass, and capacity.

Using Dimensional Analysis

A common method used to perform calculations with different units of measurement is called dimensional analysis. Dimensional analysis is a problem-solving technique where measurements are converted to equivalent units of measure by multiplying a given unit of measurement by a fractional form of 1 to obtain the desired unit of administration. This method is also referred to as creating proportions that state equivalent ratios. Equivalencies described in the Conversions section are used to set up ratios with the fractional form of 1 to achieve the desired unit the problem is asking for. The units of measure that must be eliminated to solve the problem are set up on the diagonal so that they can be cancelled out. Lines are drawn during the problem-solving process to show that cancellation has occurred. Effectively, this is the same as using cross products of a proportion to solve a problem that you reviewed in the Solve Proportions chapter.

When setting up a medication dosage calculation using dimensional analysis, it is important to begin by identifying the goal unit to be solved. After the goal unit is set, the remainder of the equation is set up using fractional forms of 1 and equivalencies to cancel out units to achieve the goal unit. It is important to understand that when using this problem-solving method, the numerator and denominator are interchangeable because they are expressing a relationship. You’ll practice using dimensional analysis to solve simple conversion problems of ounces to milliliters to demonstrate the technique.

First, watch the video Dimensional Analysis for Nurses and Nursing Students for Dosage Calculations Nursing School (10 minutes)

Conversions

Ounces to Millimeters

When caring for patients, nurses often need to convert between ounces and milliliters. Although these equivalencies are typically memorized (see Frequently Used Conversions in Nursing PDF), let’s start with a simple problem of converting ounces to milliliters to demonstrate the technique of dimensional analysis.

Practice Problem #1: Ounces to Millimeters

Sample scenario: A patient drank an 8-ounce can of juice. The nurse must document the intake in milliliters. How many milliliters of juice did the patient drink?

Here is an example of how to solve this conversion problem using dimensional analysis.

Identify the unit being solved for as the goal. In this example, we want to convert the patient’s oral intake from ounces to milliliters, so we are solving for milliliters (mL):
$mL=?$
Set up the numerator in the first fraction to match the desired unit to be solved. In this case, we want to know how many milliliters should be documented, so mL is placed in the numerator. To complete the fraction, we add information already known. In this example, we know that 30 mL is equivalent to 1 ounce, so 30 mL is added to the numerator and 1 ounce is added to the denominator:
$mL=\frac{30\text{ }mL}{1 \text{ }ounce}$
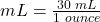
Add the second fraction to the equation. When using dimensional analysis, fractions are set up so the same units are diagonal from each other so they cancel each other out, leaving the desired unit. For this problem, the second fraction is set up to include ounces in the numerator so that it will cancel out ounces in the denominator of the first fraction. “8” is then added to the numerator because we know from the problem that the patient consumed 8 ounces. “1” is then added to the denominator because the purpose of the second fraction is to cancel out units:
$mL=\frac{30\text{ }mL}{1\text{ }ounce}\cdot \frac{8\text{ }ounces}{1}$
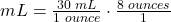
Cancel out similar units that are diagonal to each other. After canceling out ounces, we are left with our desired units of mL:
$mL=\frac{30\text{ }mL}{1\text{ }\cancel{ounce}}\cdot \frac{8\text{ }\cancel{ounces}}{1}$
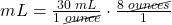
Multiply across the numerators and then multiply across the denominators:
$mL=\frac{30\text{ }mL}{1\text{ }\cancel{ounce}}\cdot \frac{8\text{ }\cancel{ounces}}{1}=\frac{30\text{ }mL\cdot8}{1\cdot1=1}=\frac{240\text{ }mL}{1}$
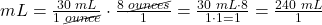
Divide the numerator by the denominator to get the final answer with the desired goal unit:
$\frac{240\text{ }mL}{1}=240\text{ }mL$

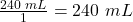
Practice Problem #2: Ounces to Milliliters

In a similar manner, dimensional analysis can be used to calculate a patient’s total liquid intake on their meal tray. See Figure 5.6 for an example of a patient’s meal tray in a hospital setting.

A patient's meal tray containing an entree, side dishes, dessert, and a serving of orange juice. — *Figure 5.6: Meal Tray*

Sample scenario: Your patient consumed 8 ounces of coffee, 4 ounces of orange juice, and 4 ounces of milk. How many milliliters of intake will you document?

Calculate using dimensional analysis.

Add up the total intake in ounces:
$8+4+4=16\text{ }ounces$
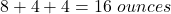
Start by identifying mL as the goal unit for which you are solving. In this case, we want to know the number of milliliters:
$mL=?$
Create the first fraction by matching milliliters in the numerator. Then, using known equivalency that 30 mL is equal to 1 ounce, place 30 in the numerator and 1 ounce in the denominator:
$mL=\frac{30\text{ }mL}{1 \text{ }ounce}$
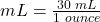
Create the second fraction to cross out units. You know you want to cross out ounces, so place ounces in the numerator. Then, add the known amount of ounces consumed, which was 16:
$mL=\frac{30\text{ }mL}{1 \text{ }ounce}\cdot\frac{16\text{ }ounces}{1}$
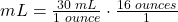
Multiply across the numerators and then the denominators. Divide the numerator by the denominator of 1 for the final answer in mL:
$mL=\frac{30\text{ }mL}{1 \text{ }\cancel{ounce}}\cdot\frac{16\text{ }\cancel{ounces}}{1}=30\text{ }mL\cdot16=480\text{ }mL$

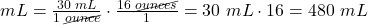
Optional: For similar practice problems, watch Intake and Output Nursing Calculation Practice Problems (9-minute video).

Pounds to Kilograms

Exercises

Converting pounds to kilograms is typically memorized as an equivalency, but let’s practice using the technique of dimensional analysis. This time, we summarize the process and show the entire calculation on one line.

Sample scenario: The patient entered their weight as 137 pounds on their intake form. Convert the patient’s weight to kilograms to document it in the electronic medical record. Round your answer to the nearest tenth. Calculate using dimensional analysis.

Start by identifying kg as the goal unit for which you are solving. Then, set up the first fraction so that the numerator matches the goal unit of kg. For the denominator, add 2.2 lbs because the known equivalency is 1 kg is equivalent to 2.2 pounds. Set up the second fraction with pounds in the numerator so that pounds will cross out diagonally to eliminate this unit. Then, add the patient’s known weight (137 lb) in the numerator, with 1 in the denominator because the function of this fraction is to cross out units. Multiply across the numerators and then the denominators. Finally, divide the final fraction to solve the problem, and round the answer to the nearest tenth of a kilogram.

$kg=\frac{1\text{ }kg}{22\text{ }\cancel{lb}}\cdot\frac{137\text{ }\cancel{lb}}{}=\frac{137\text{ }kg}{2.2}=62.2727\text{ }kg=62.3\text{ }kg$

What’s Next?

You reviewed solving proportions in preparation for this Dimensional Analysis chapter. Here are some examples of more ways you will apply these techniques in Nursing school:

When tablets are prescribed for a patient, the dosage of the tablets supplied is often different from the prescription, and nurses must calculate the number of tablets to administer.
Medications can also be supplied in liquid instead of tablets or capsules. Liquid concentrations are typically provided in milligrams (mg) per a given number of milliliters (mL). The nurse must calculate how many milliliters (mL) to administer based on the prescribed dose in milligrams (mg).
Liquid medications are often prescribed based on the patient’s weight. Nurses can use dimensional analysis to determine the amount of liquid medication the patient will receive based on their weight, the provider order, and the concentration of medication supplied.
Safe ranges of dosages are provided in drug reference materials. Medication errors often occur in children, who have smaller ranges of safe dosage than adults due to their smaller weight. Nurses can use dimensional analysis to double-check that the medication dosage to be administered falls within a safe range for the patient.
Medications can also be administered intravenously (IV). Dimensional analysis plays a role in the math calculations related to IV medication administration. Nurses ultimately ensure that our patients are receiving the correct dose over the correct period of time to avoid adverse effects from too-rapid or too-slow intravenous administration.
In addition to calculating IV flow rates, nurses also commonly calculate when an infusion will be completed so they will know when to discontinue the infusion or hang another IV bag.

Chapter Attributions

This chapter was adapted by Cheryl Colan and Fatima Baig from the 5.6 Using Dimensional Analysis and 5.7 Conversions sections in “Nursing Skills [Internet],” Kimberly Ernstmeyer and Elisabeth Christman, editors. Licensed under a CC BY 4.0 license.

Media Attributions

Dimensional Analysis for Nurses & Nursing Students for Dosage Calculations Nursing School by RegisteredNurseRN is licensed under the Standard YouTube license.

License

Icon for the Creative Commons Attribution 4.0 International License