Ratios
Ratios are numbers that are used in nursing to compare two numbers that have a relationship to each other. In nursing practice, there are many numbers that are related to each other. For example, 50 milligrams are contained in each vial.
Learning Objectives
By the end of this section, you will be able to:
Write a Ratio as a Fraction
When you apply for a mortgage, the loan officer will compare your total debt to your total income to decide if you qualify for the loan. This comparison is called the debt-to-income ratio. A ratio compares two quantities that are measured with the same unit. If we compare 𝑎 and 𝑏, the ratio is written as ![]() to
to ![]() ,
, ![]() , or
, or ![]() .
.
RATIOS
A ratio compares two numbers or two quantities that are measured with the same unit.
The ratio of ![]() to
to ![]() is written
is written ![]() to
to ![]() ,
, ![]() , or
, or ![]() ..
..
In this section, we will use the fraction notation. When a ratio is written in fraction form, the fraction should be simplified. If it is an improper fraction, we do not change it to a mixed number. Because a ratio compares two quantities, we would leave a ratio as ![]() instead of simplifying it to
instead of simplifying it to ![]() so that we can see the two parts of the ratio.
so that we can see the two parts of the ratio.
Example 5.58: Write each ratio as a fraction.
Write each ratio as a fraction of whole numbers:
- ⓐ
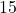 to
to 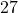
- ⓑ
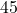 to
to 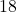
Solution:
| ⓐ |
|
| Write as a fraction with the first number in the numerator and the second number in the denominator. | |
| Simplify the fraction. |
| ⓑ |
|
| Write as a fraction with the first number in the numerator and the second number in the denominator. | |
| Simplify. |
We leave the ratio in ⓑ as an improper fraction.
Try It: Write each ratio as a fraction.
Applications of Ratios
One real-world application of ratios that affects many people involves measuring cholesterol in blood. The ratio of total cholesterol to HDL cholesterol is one way doctors assess a person’s overall health. A ratio of less ![]() to
to ![]() is considered good.
is considered good.
Example 5.6.1
Hector’s total cholesterol is ![]() mg/dl and his HDL cholesterol is
mg/dl and his HDL cholesterol is ![]() mg/dl.
mg/dl.
- ⓐ Find the ratio of his total cholesterol to his HDL cholesterol.
- ⓑ Assuming that a ratio less than
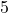 to
to 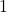 is considered good, what would you suggest to Hector?
is considered good, what would you suggest to Hector?
Solution:
ⓐ First, write the words that express the ratio. We want to know the ratio of Hector’s total cholesterol to his HDL cholesterol.
| Write as a fraction. | |
| Substitute Hector’s values. | |
| Simplify the fraction. |
ⓑ Is Hector’s cholesterol ratio ok? If we divide ![]() by
by ![]() , we obtain approximately
, we obtain approximately ![]() , so
, so ![]() .
.
Now compare Hector’s value to the ratio that is considered good: ![]() .
.
Hector’s cholesterol ratio is high! Hector should either lower his total cholesterol or raise his HDL cholesterol.
Try It: Ratio of Total cholesterol to HDL cholesterol
Ratios of Two Measurements in Different Units
To find the ratio of two measurements, we must make sure the quantities have been measured with the same unit. If the measurements are not in the same units, we must first convert them to the same units.
We know that to simplify a fraction, we divide out common factors. Similarly, in a ratio of measurements, we divide out the common unit.
Example 5.6.2
The Americans with Disabilities Act (ADA) Guidelines for wheelchair ramps require a maximum vertical rise of ![]() inch for every
inch for every ![]() foot of horizontal run. What is the ratio of the rise to the run?
foot of horizontal run. What is the ratio of the rise to the run?
Solution:
In a ratio, the measurements must be in the same units. We can change feet to inches, or inches to feet. It is usually easier to convert to the smaller unit, since this avoids introducing more fractions into the problem.
Write the words that express the ratio.
| We need: | Ratio of the rise to the run. |
| Write the ratio as a fraction. | |
| Substitute in the ADA’s values. | |
| Convert 1 foot to inches, the smaller unit. | |
| Simplify the fraction, dividing out common factors and common units. |
So the ratio of rise to run is ![]() to
to ![]() . This means that the ramp should rise
. This means that the ramp should rise ![]() inch for every
inch for every ![]() inches of horizontal run to comply with the guidelines.
inches of horizontal run to comply with the guidelines.
Try It: Ratio of Two Measurements in Different Units
Write a Rate as a Fraction
Frequently, we want to compare two different types of measurements, such as miles to gallons. To make this comparison, we use a rate. Examples of rates are ![]() miles in
miles in ![]() hours,
hours, ![]() words in
words in ![]() minutes, and
minutes, and ![]() dollars per
dollars per ![]() ounces.
ounces.
Rate
A rate compares two quantities of different units. A rate is usually written as a fraction.
When writing a fraction as a rate, we put the first given amount with its units in the numerator and the second amount with its units in the denominator. When rates are simplified, the units remain in the numerator and denominator.
Example 5.6.3
Bob drove his car 525 miles in 9 hours. Write this rate as a fraction.
Solution:
| Write down the rate. | 525 miles in 9 hours |
| Write as a fraction, with 525 miles in the numerator and 9 hours in the denominator. | |
| Simplify the fraction, dividing out common factors. |
So ![]() miles in
miles in ![]() hours is equivalent to
hours is equivalent to ![]() .
.
Try It: Write rates as fractions
Find Unit Rates
In the last example, we calculated that Bob was driving at a rate of ![]() . This tells us that every three hours, Bob will travel
. This tells us that every three hours, Bob will travel ![]() miles. miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate with a denominator of
miles. miles. This is correct, but not very useful. We usually want the rate to reflect the number of miles in one hour. A rate with a denominator of ![]() unit is referred to as a unit rate.
unit is referred to as a unit rate.
Unit Rate
A unit rate is a rate with a denominator of ![]() unit.
unit.
Unit rates are very common in our lives. For example, when we say that we are driving at a speed of 68 miles per hour, we mean that we travel 68 miles in 1 hour. We would write this rate as 68 miles/hour (read “68 miles per hour”). The common abbreviation for this is 68 mph. Note that when no number is written before a unit, it is assumed to be 1.
So 68 miles/hour really means 68 miles/1 hour.
Two rates we often use when driving can be written in different forms, as shown:
| Example | Rate | Write | Abbreviate | Read |
|---|---|---|---|---|
| 68 mph | 68 miles per hour | |||
| 36 mpg | 36 miles per gallon |
Another example of unit rate that you may already know about is hourly pay rate. It is usually expressed as the amount of money earned for one hour of work. For example, if you are paid ![]() for each hour you work, you could write that your hourly (unit) pay rate is
for each hour you work, you could write that your hourly (unit) pay rate is ![]() /hour (read “
/hour (read “![]() per hour”).
per hour”).
To convert a rate to a unit rate, we divide the numerator by the denominator. This gives us a denominator of ![]() .
.
Example 5.6.4
Anita was paid ![]() last week for working
last week for working ![]() hours.
hours.
Solution:
| Start with a rate of dollars to hours. | |
| Write as a rate. | |
| Divide the numerator by the denominator. | |
| Rewrite as a rate |
Anita’s hourly pay rate is ![]() /hour.
/hour.
Try It: Find unit rates (dollars per hour).
Example 5.6.5
Sven drives his car ![]() miles, using
miles, using ![]() gallons of gasoline. How many miles per gallon does his car get?
gallons of gasoline. How many miles per gallon does his car get?
Solution:
| Start with a rate of miles to gallons. | |
| Write as a rate. | |
| Divide 455 by 14 to get the unit rate. |
Sven’s car gets ![]() miles/gallon, or
miles/gallon, or ![]() mpg.
mpg.
Try It: Find Unit Rates (miles per gallon).
Translate Phrases to Expressions with Fractions
Have you noticed that the examples in this section used the comparison words ratio of, to, per, in, for, on, and from? When you translate phrases that include these words, you should think either ratio or rate. If the units measure the same quantity (length, time, etc.), you have a ratio. If the units are different, you have a rate. In both cases, you write a fraction.
Example 5.6.8
Translate the word phrase into an algebraic expression. In all 3 examples, the units measure different quantities, so the expression will be a rate.
- ⓐ
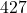 miles per
miles per 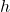 hours
hours - ⓑ
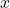 students to
students to 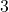 teachers
teachers - ⓒ
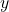 dollars for
dollars for 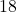 hours
hours
Solution:
| ⓐ | |
| Write as a rate. |
| ⓑ | |
| Write as a rate. |
| ⓒ | |
| Write as a rate. |
Try It: Translate word phrases into algebraic expressions with fractions.
Practice Makes Perfect
Write a Ratio as a Fraction
Practice writing ratios as fractions.
Write a Rate as a Fraction
Practice writing rates as fractions.
Find Unit Rates
Practice finding unit rates.
Translate Phrases to Expressions with Fractions
Practice translating phrases to expressions with fractions.
Self Check
After completing the exercises, use this table to evaluate your mastery of the objectives of this section. For each skill listed in a table row, rate yourself in the column that best describes your confidence level.
| I can … | Confidently | With some help | No – I don’t get it! |
|---|---|---|---|
| write a ratio as a fraction. | |||
| write a rate as a fraction. | |||
| find unit rates. | |||
| translate phrases to expressions with fractions. |
If most of your checks were:
- …confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident in your ability to do these things? Be specific.
- …with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, and in nursing, every topic builds upon previous work. It is important to ensure you have a strong foundation before you move on. Who can you ask for help? Is there a place on campus where math tutors are available? Can your study skills be improved?
- …no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor, student success specialist, or math tutor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Chapter Attributions
This chapter was adapted by Corinn Herrell and Cheryl Colan from “5.6 Ratios and Rate” in Prealgebra 2e by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis. Licensed under a CC BY 4.0 license.

