Systems of Measurement
Safe medication administration is based on the safe calculation of drug dosages. In this chapter, you will be introduced to foundational knowledge for working with both the metric system and the household system in the calculation of drug dosages. Understanding and working with the systems of measurement commonly used in health care is an essential component of nursing.
Learning Objectives
By the end of this section, you will be able to:
- Make unit conversions in the U.S. system
(pounds, teaspoons, tablespoons, cups, ounces) - Make unit conversions in the metric system
(micrograms, milligrams, milliliters, liters, cubic centimeters, kilograms, grams) - Convert between the U.S. and the metric systems of measurement
- Convert between Fahrenheit and Celsius temperatures
- Use military time
- Convert between military and traditional time
In this section, we will see how to convert different types of units, such as feet to miles or kilograms to pounds. The basic idea in all of the unit conversions will be to use a form of ![]() , the multiplicative identity, to change the units but not the value of a quantity.
, the multiplicative identity, to change the units but not the value of a quantity.
Make Unit Conversions in the U.S. System
There are two systems of measurement commonly used around the world. Most countries use the metric system. The United States uses a different system of measurement, usually called the U.S. system. We will look at the U.S. system first.
The U.S. system of measurement uses units of inch, foot, yard, and mile to measure length, and pound and ton to measure weight. For capacity, the units used are teaspoon, tablespoon, ounce, cup, pint, quart, and gallon.
Both the U.S. system and the metric system measure time in seconds, minutes, or hours.
The equivalencies among the basic units of the U.S. system of measurement are listed in Table 7.2. The table also shows, in parentheses, the common abbreviations for each measurement.
In many real-life applications, we need to convert between units of measurement. We will use the identity property of multiplication to make these conversions. We’ll restate the Identity Property of Multiplication here for easy reference.
Identity Property of Multiplication:
For any real number ![]() ,
, ![]() and
and ![]()
To use the identity property of multiplication, we write ![]() in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that
in a form that will help us convert the units. For example, suppose we want to convert inches to feet. We know that ![]() foot is equal to
foot is equal to ![]() inches, so we can write
inches, so we can write ![]() as the fraction
as the fraction ![]() . When we multiply by this fraction, we do not change the value but just change the units.
. When we multiply by this fraction, we do not change the value but just change the units.
But ![]() also equals
also equals ![]() . How do we decide whether to multiply by
. How do we decide whether to multiply by ![]() or
or ![]() . We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert
. We choose the fraction that will make the units we want to convert from divide out. For example, suppose we wanted to convert ![]() inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.
inches to feet. If we choose the fraction that has inches in the denominator, we can eliminate the inches.
![]()
On the other hand, if we wanted to convert ![]() feet to inches, we would choose the fraction that has feet in the denominator.
feet to inches, we would choose the fraction that has feet in the denominator.
![]()
We treat the unit words like factors and ‘divide out’ common units like we do common factors.
HOW TO: Make unit conversions.
Steps:
- Multiply the measurement to be converted by 1; write 1 as a fraction relating the units given and the units needed.
- Multiply.
- Simplify the fraction, performing the indicated operations and removing the common unit
Practice
When we use the Identity Property of Multiplication to convert units, we need to make sure the units we want to change from will divide out. Usually, this means we want the conversion fraction to have those units in the denominator.
Examples
Ndula, an elephant at the San Diego Safari Park, weighs almost 3.2 tons. Convert her weight to pounds.
Practice
Sometimes to convert from one unit to another, we may need to use several other units in between, so we will need to multiply several fractions.
Example 7.46
Juliet is going with her family to their summer home. She will be away for 9 weeks. Convert the time to minutes.
Practice
Examples
How many fluid ounces are in 1 gallon of milk?
Exercises
Make Unit Conversions in the Metric System
In the metric system, units are related by powers of 10. The root words of their names reflect this relation. For example, the basic unit for measuring length is a meter. One kilometer is 1000 meters; the prefix kilo- means thousand.
One centimeter is ![]() of a meter because the prefix centi- means one one-hundredth (just like one cent is
of a meter because the prefix centi- means one one-hundredth (just like one cent is ![]() of one dollar).
of one dollar).
The equivalencies of measurements in the metric system are shown in Table 7.3. The common abbreviations for each measurement are given in parentheses.
To make conversions in the metric system, we will use the same technique we did in the U.S. system. Using the identity property of multiplication, we will multiply by a conversion factor of one to get to the correct units.
Points to Remember for Nursing
- The liter and gram are the basic units used for medication administration.
- Values at 1,000 or greater than 1,000 should be written with a comma.
- Express answers using the following rules of the metric system:
- Fractional metric units are expressed as decimals.
- Place a leading zero in front of the decimal point when the quantity is less than a whole number to prevent potential dosage errors.
- Omit trailing zeros to avoid misreading a value and making a potential error in dosage.
- The abbreviation for a measure is placed after the quantity.
- Place a full space between the numeral and the measure’s abbreviation.
- Use standard International Systems of Units (SI) abbreviations.
Have you ever run a 5 k or 10 k race? The lengths of those races are measured in kilometers. The metric system is commonly used in the United States when talking about the length of a race.
Example 7.50
Nick ran a 10-kilometer race. How many meters did he run?
Practice converting between metric system length units.
Practice converting between metric mass/weight units.
Since the metric system is based on multiples of ten, conversions involve multiplying by multiples of ten. In Decimals, we learned how to simplify these calculations by just moving the decimal.
To multiply by 10, 100, or 1000, we move the decimal to the right 1, 2, or 3 places, respectively. To multiply by 0.1, 0.01, or 0.001, we move the decimal to the left 1, 2, or 3 places, respectively.
We can apply this pattern when we make measurement conversions in the metric system.
In Example 7.51, we changed 3200 grams to kilograms by multiplying by ![]() (or 0.001). This is the same as moving the decimal 3 places to the left.
(or 0.001). This is the same as moving the decimal 3 places to the left.
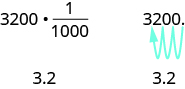
Example 7.52
Convert:
- ⓐ 350 liters to kiloliters
- ⓑ 4.1 liters to milliliters.
Solution:
ⓐ We will convert liters to kiloliters. In Table 7.3, we see that 1 kiloliter = 1,000 liters.
| Start with the quantity you want to convert. | 350 L |
| Multiply by 1, writing 1 as a fraction relating liters to kiloliters. | |
| Simplify by canceling out the like units. | |
| Move the decimal 3 units to the left (or divide 350 by 1,000). | 0.35 kL |
So, 350 L = 0.35 kL.
ⓑ We will convert liters to milliliters. In Table 7.3, we see that 1 liter = 1,000 milliliters.
| Start with the quantity you want to convert. | |
| Multiply by 1, writing 1 as a fraction relating milliliters to liters. | |
| Simplify by canceling out the like units. | |
| Move the decimal 3 units to the right (or multiply 4.1 by 1,000). |
So, 4.1 L = 4,100 mL.
Practice converting between metric units of volume/capacity.
Convert Between U.S. and Metric Systems of Measurement
Many measurements in the United States are made in metric units. A drink may come in 2-liter bottles, calcium may come in 500 mg capsules, and we may run a 5 K race. To work easily in both systems, we need to be able to convert between the two systems.
Table 7.4 shows some of the most common conversions.
We make conversions between the systems just as we do within the systems—by multiplying by unit conversion factors.
Lee’s water bottle holds 500 mL of water. How many fluid ounces are in the bottle? Round to the nearest tenth of an ounce.
Solution:
| Start with the quantity you want to convert. | |
| Multiply by a unit conversion factor relating mL and ounces. | |
| Simplify. | |
| Divide. | |
| Round to the nearest tenth of an ounce. |
The water bottle holds 16.7 fluid ounces.
Practice converting between U.S. and metric units of volume/capacity.
The conversion factors in Table 7.4 are not exact, but the approximations they give are close enough for everyday purposes. In Example 7.55, we rounded the number of fluid ounces to the nearest tenth.
Example 7.56
Soleil lives in Minnesota but often travels in Canada for work. While driving on a Canadian highway, she passes a sign that says the next rest stop is in 100 kilometers. How many miles until the next rest stop? Round your answer to the nearest mile.
Solution:
| Start with the quantity you want to convert. | |
| Multiply by a unit conversion factor relating kilometers and miles. | |
| Cancel out the common units. | |
| Simplify. | |
| Divide, rounding to the nearest mile. |
It is about 62 miles to the next rest stop.
Practice converting between U.S. and metric units of length/distance.
Convert Between Fahrenheit and Celsius Temperatures
In a medical setting, vital signs are usually measured at the start of an appointment. Has a medical assistant ever taken your temperature and told you it was 37℃? What does that mean?
The U.S. and metric systems use different scales to measure temperature. The U.S. system uses degrees Fahrenheit, written ℉. The metric system uses degrees Celsius, written ℃. Figure 7.9 shows the relationship between the two systems.
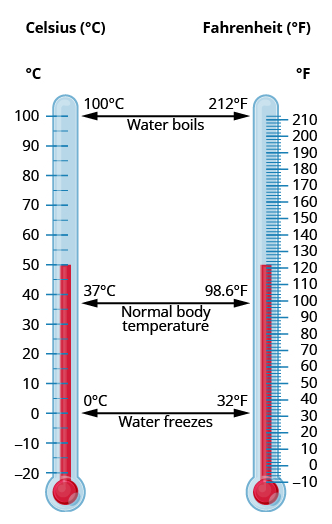
If we know the temperature in one system, we can use a formula to convert it to the other system.
Temperature Conversion Formulas
To convert from Fahrenheit temperature, ![]() , to Celsius temperature,
, to Celsius temperature, ![]() , use the formula:
, use the formula:
![]()
To convert from Celsius temperature, ![]() , to Fahrenheit temperature,
, to Fahrenheit temperature, ![]() , use the formula:
, use the formula:
![]()
Example 7.57
Convert ![]() into degrees Celsius.
into degrees Celsius.
Solution:
We will substitute ![]() into the formula to find
into the formula to find ![]() .
.
| Use the formula for converting |
|
| In the formula, substitute 50 for |
|
| Simplify in parentheses. | |
| Multiply. |
A temperature of ![]() is equivalent to
is equivalent to ![]() .
.
Practice converting Fahrenheit temperatures to degrees Celsius.
Examples 7.58
The weather forecast for Paris predicts a high of ![]() . Convert the temperature into degrees Fahrenheit.
. Convert the temperature into degrees Fahrenheit.
Solution:
We will substitute ![]() into the formula to find
into the formula to find ![]() .
.
| Use the formula for converting |
|
| In the formula, substitute 20 for |
|
| Multiply. | |
| Add. |
So ![]() is equivalent to
is equivalent to ![]() .1
.1
Practice converting Celsius temperatures to degrees Fahrenheit.
Use Military Time
Military time is a method of measuring the time based on the full 24 hours of the day rather than two groups of 12 hours indicated by AM and PM. It is also referred to as using a 24-hour clock.
Using military time is the standard method medical professionals use to indicate time for medication administration. The use of military time reduces potential confusion that may be caused by using AM and PM, and also avoids potential duplication when giving scheduled medications.
In military time, each hour of the day has a unique number from 1 to 24, and no colons are used to separate hours from minutes. For example, instead of stating medication is due at 7 AM and 7 PM, it is documented on the medication administration record as due at 0700 and 1900. See Figure 7.10 for an example clock that displays both standard and military time.

Convert Between Traditional and Military Time
Conversion of an AM time to military time simply involves removing the colon and, if the hour is a single digit, adding a zero to the front of the hour. For example, 6:30 AM becomes 0630. For two-digit hours, no zero is added. For example, 11:30 AM becomes 1130.
Conversion of a PM time involves removing the colon and adding 1200 to the time. Another way to think of this is adding 12 to the hour’s number. For example, 7:15 PM becomes 1915. 11:15 PM becomes 2315.
When using military time in verbal speech, morning hours are pronounced beginning with “zero” or “O.” For example, 7:00 a.m. is pronounced “zero seven hundred” or “oh seven hundred.” The time of 2:43 p.m. is pronounced “fourteen forty-three.” See Table 7.5 for a military time conversion chart.
| 12-hour Clock Time | Military/24-hour Clock Time | 12-hour Clock Time | Military/24-hour Clock Time |
|---|---|---|---|
| 12:00 AM | 0000 | 12:00 PM | 1200 |
| 1:00 AM | 0100 | 1:00 PM | 1300 |
| 2:00 AM | 0200 | 2:00 PM | 1400 |
| 3:00 AM | 0300 | 3:00 PM | 1500 |
| 4:00 AM | 0400 | 4:00 PM | 1600 |
| 5:00 AM | 0500 | 5:00 PM | 1700 |
| 6:00 AM | 0600 | 6:00 PM | 1800 |
| 7:00 AM | 0700 | 7:00 PM | 1900 |
| 8:00 AM | 0800 | 8:00 PM | 2000 |
| 9:00 AM | 0900 | 9:00 PM | 2100 |
| 10:00 AM | 1000 | 10:00 PM | 2200 |
| 11:00 AM | 1100 | 11:00 PM | 2300 |
Example: Converting from traditional time to military time.
Nurse Jamie is preparing to educate a patient who will receive medication according to a strict schedule. The medication needs to be given at the following times:
- First dose at 1430
- Second dose at 0645 the next day
Nurse Jamie needs to convert these military times to a 12-hour format to ensure the patient understands when to expect their doses.
- ⓐ What is the 12-hour time format for the first dose?
- ⓑ What is the 12-hour time format for the second dose?
Solution:
ⓐ Convert 1430 to 12-hour format.
| Start with military/24-hour format. | 1430 |
| Subtract 12 from the hour to convert the time to 12-hour format. | |
| Substitute hour, add the colon, and indicate AM or PM. | 1430 = 2:30 PM |
Nurse Jamie will tell the patient to expect their first dose at 2:30 PM.
ⓑ Convert 0645 to 12-hour format.
| Start with military/24-hour format. | 0645 |
| Since 0645 is in the morning, it remains the same. Add the colon, and indicate AM or PM. | 0645 = 6:45 AM |
Nurse Jamie will tell the patient to expect their second dose at 6:45 AM.
Try It: Convert between traditional and military time.
Access Additional Online Video Resources
Equivalencies to Memorize
In nursing, we use multiple conversions during patient care. Here is a page of common conversions with their associated abbreviations that we highly recommend you memorize prior to school.
Common Conversions for Nursing
Practice Makes Perfect
Practice: Make unit conversions in the U.S. System
In the following exercises, convert the units.
Practice: Make Unit conversions in the Metric System
In the following exercises, convert the units.
Practice: Convert between U.S. and Metric Systems
In the following exercises, make the unit conversions. Round to the nearest tenth.
Practice: Convert between Fahrenheit and Celsius
Practice: Convert between traditional and military time.
Everyday Math
Self Check
After completing the exercises, use this table to evaluate your mastery of the objectives of this section. For each skill listed in a table row, rate yourself in the column that best describes your confidence level.
| I can … | Confidently | With some help | No – I don’t get it! |
|---|---|---|---|
| make unit conversions in the U.S. system. | |||
| make unit conversions in the metric system. | |||
| convert between the U.S. and the metric systems of measurement. | |||
| convert between Fahrenheit and Celsius temperatures. | |||
| use military time. | |||
| convert between traditional and military time. |
If most of your checks were:
- …confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident in your ability to do these things? Be specific.
- …with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, and in nursing, every topic builds upon previous work. It is important to ensure you have a strong foundation before you move on. Who can you ask for help? Is there a place on campus where math tutors are available? Can your study skills be improved?
- …no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor, student success specialist, or math tutor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Chapter Attributions
This chapter was adapted by Corinn Herrell and Cheryl Colan from “7.5 Systems of Measurement” in Prealgebra 2e by Lynn Marecek, MaryAnne Anthony-Smith, and Andrea Honeycutt Mathis. Licensed under a CC BY 4.0 license.
The Military Time section of this chapter was adapted by Cheryl Colan from “5.3 Military Time” in Nursing Skills – 2e by Open Resources for Nursing (Open RN), published by Chippewa Valley Technical College. Licensed under a CC BY 4.0 license.
Media Attributions
Military Time Clock by Deanna Hoyord for Chippewa Valley Technical College is licensed under a CC BY 4.0 license.
A standard for recording time that avoids confusion between daytime and nighttime hours because each hour of the day is represented by a number ranging from 0000 to 2359.

