Whole Numbers
Nurses use whole numbers for medication administration, dosage calculation, patient tracking, and many other tasks.To perform these tasks, the nurse needs to understand the concept of whole numbers. Whole numbers are non-negative numbers without any fractional or decimal parts. They start from 0 and go up indefinitely (0, 1, 2, 3, …). They do not have parts like fractions and decimals do such as 2.5 or ⅖.
Learning Objectives
By the end of this section, you will be able to:
- Identify the place value of a digit
- Use place value to name whole numbers
- Use place value to write whole numbers
- Round whole numbers to a specified place value
Use Place Value with Whole Numbers
The most basic numbers used are the numbers we use to count objects in our world: 1, 2, 3, 4, and so on. These are called the counting numbers. Counting numbers are also called natural numbers. If we add zero to the counting numbers, we get the set of whole numbers.
![]() Counting Numbers: 1, 2, 3, …
Counting Numbers: 1, 2, 3, …
![]() Whole Numbers: 0, 1, 2, 3, …
Whole Numbers: 0, 1, 2, 3, …
The notation “…” is called ellipsis and means “and so on,” or that the pattern continues endlessly.
We can visualize counting numbers and whole numbers on a number line. See Figure 1.
The numbers on the number line get larger as they go from left to right, and smaller as they go from right to left. While this number line shows only the whole numbers 0 through 6, the numbers keep going without end.

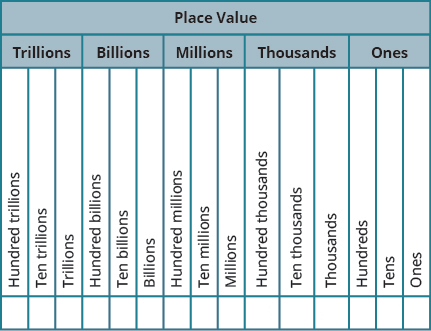
Our number system is called a place value system, because the value of a digit depends on its position in a number. Figure 2 shows the place values. The place values are separated into groups of three, which are called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.
The number 5,278,194 is shown in the chart. The digit 5 is in the millions place. The digit 2 is in the hundred-thousands place. The digit 7 is in the ten-thousands place. The digit 8 is in the thousands place. The digit 1 is in the hundreds place. The digit 9 is in the tens place. The digit 4 is in the ones place.
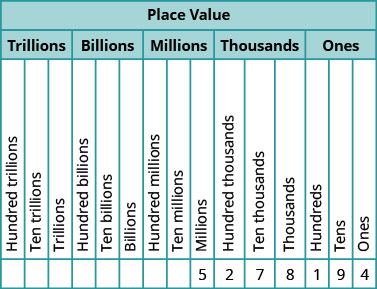
EXAMPLE 1
In the number 63,407,218, find the place value of each digit:
- 7
- 0
- 1
- 6
- 3
Place the number in the place value chart:
a) The 7 is in the thousands place.
b) The 0 is in the ten thousands place.
c) The 1 is in the tens place.
d) The 6 is in the ten-millions place.
e) The 3 is in the millions place.
TRY IT 1.1
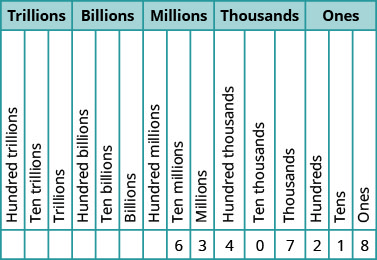
TRY IT 1.2

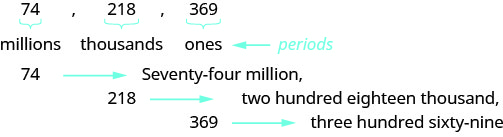
When you write a check, you write out the number in words as well as in digits. To write a number in words, write the number in each period, followed by the name of the period, without the s at the end. Start at the left, where the periods have the largest value. The ones period is not named. The commas separate the periods, so wherever there is a comma in the number, put a comma between the words (see Figure 3). The number 74,218,369 is written as seventy-four million, two hundred eighteen thousand, three hundred sixty-nine.
HOW TO: Name a Whole Number in Words.
- Start at the left and name the number in each period, followed by the period name.
- Put commas in the number to separate the periods.
- Do not name the ones period.
EXAMPLE 2
Name the number 8,165,432,098,710 using words.
Name the number in each period, followed by the period name.
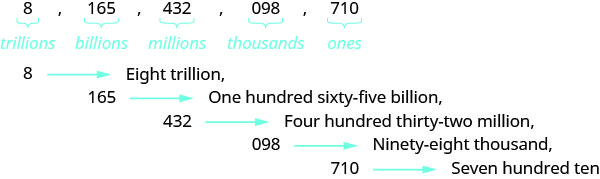
Put the commas in to separate the periods.
So, ![]() is named as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.
is named as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.
TRY IT 2.1

TRY IT 2.2

HOW TO: Write a Whole Number Using Digits.
- Identify the words that indicate periods. (Remember, the ones period is never named.)
- Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
- Name the number in each period and place the digits in the correct place value position.
EXAMPLE 3
Write nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine as a whole number using digits.
Identify the words that indicate periods.
Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
Then write the digits in each period.

The number is 9,246,073,189.
TRY IT 3.1
TRY IT 3.2
In 2022, The United States Census Bureau estimated the population of Phoenix as 1,644,409. We could say the population of Phoenix was approximately 1.6 million. In many cases, you don’t need the exact value; an approximate number is good enough.
The process of approximating a number is called rounding. Numbers are rounded to a specific place value, depending on how much accuracy is needed. Saying that the population of Phoenix is approximately 1.6 million means that we rounded to the hundred thousands place.
EXAMPLE 4
Round 23,658 to the nearest hundred.
| Step | Example | Demonstration |
|---|---|---|
|
1. Locate the given place value with an arrow. All digits to the left do not change. |
Locate the hundreds place in 23,658. |  |
|
2. Underline the digit to the right of the given place value. |
Underline the 5, which is to the right of the hundreds place (in the tenths place). |  |
|
3. Is this digit greater than or equal to 5? |
Add 1 to the 6 in the hundreds place, since 5 is greater than or equal to 5. |  |
|
4. Replace all digits to the right of the given place value with zeros. |
Replace all digits to the right of the hundreds place with zeros. | 
So, 23,658 rounded to the nearest hundred is 23,700. |
TRY IT 4.1
TRY IT 4.2
HOW TO: Round Whole Numbers.
- Locate the given place value and mark it with an arrow. All digits to the left of the arrow do not change.
- Underline the digit to the right of the given place value.
- Is this digit greater than or equal to 5?
- Yes–add
 to the digit in the given place value.
to the digit in the given place value. - No–do not change the digit in the given place value.
- Yes–add
- Replace all digits to the right of the given place value with zeros.
EXAMPLE 5
Round ![]() to the nearest:
to the nearest:
- hundred
- thousand
- ten thousand
a)
| Locate the hundreds place in 103,978. |  |
| Underline the digit to the right of the hundreds place. |  |
| Since 7 is greater than or equal to 5, add 1 to the 9. Replace all digits to the right of the hundreds place with zeros. | 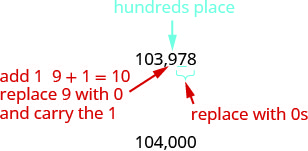
So, 103,978 rounded to the nearest hundred is 104,000. |
b)
| Locate the thousands place and underline the digit to the right of the thousands place. |  |
| Since 9 is greater than or equal to 5, add 1 to the 3. Replace all digits to the right of the hundreds place with zeros. | 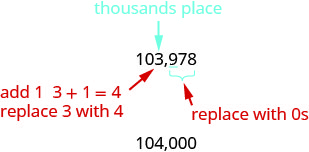
So, 103,978 rounded to the nearest thousand is 104,000. |
c)
| Locate the ten thousands place and underline the digit to the right of the ten thousands place. | 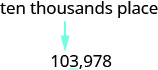 |
| Since 3 is less than 5, we leave the 0 as is, and then replace the digits to the right with zeros. | So, 103,978 rounded to the nearest ten thousand is 100,000. |
TRY IT 5.1
TRY IT 5.2
Key Concepts
- Place Value as in Figure 2.
- Name a Whole Number in Words
- Start at the left and name the number in each period, followed by the period name.
- Put commas in the number to separate the periods.
- Do not name the ones period.
- Write a Whole Number Using Digits
- Identify the words that indicate periods. (Remember the ones period is never named.)
- Draw 3 blanks to indicate the number of places needed in each period. Separate the periods by commas.
- Name the number in each period and place the digits in the correct place value position.
- Round Whole Numbers
- Locate the given place value and mark it with an arrow. All digits to the left of the arrow do not change.
- Underline the digit to the right of the given place value.
- Is this digit greater than or equal to 5?
- Yes—add 1 to the digit in the given place value.
- No—do not change the digit in the given place value.
- Replace all digits to the right of the given place value with zeros.
Glossary
-
- counting numbers
- The counting numbers are the numbers 1, 2, 3, …
- whole numbers
- The whole numbers are the numbers 0, 1, 2, 3, ….
Practice Makes Perfect
Use Place Value with Whole Numbers
PRACTICE: Find the place value of each digit in the given numbers.
PRACTICE: Name the numbers using words.
PRACTICE: Write numbers using digits.
PRACTICE: Round numbers to the specified place.
PRACTICE: Everyday math.
Chapter Attributions
This chapter was adapted by Cheryl Colan from “1.1 Whole Numbers” in Introductory Algebra by Izabela Mazur. Licensed under a CC BY 4.0 license.

