Numbers in Astronomy – Powers of Ten

112 Numbers in Astronomy – Powers of Ten

In astronomy we deal with distances on a scale you may never have thought about before, with numbers larger than any you may have encountered. We adopt two approaches that make dealing with astronomical numbers a little bit easier. First, we use a system for writing large and small numbers called scientific notation (or sometimes powers-of-ten notation). This system is very appealing because it eliminates the many zeros that can seem overwhelming to the reader. In scientific notation, if you want to write a number such as 500,000,000, you express it as 5 × 10⁸. The small raised number after the 10 is called an exponent, and it helps up keep track of how large – or small – the number is. The 10⁸ lets us know that the 5 means “five hundred million”, not just “five”.

The second way we try to keep numbers simple is with units of measurement. Scientists across the disciplines have a adopted a consistent set of units—the metric International System of Units, or SI (from the French Système International d’Unités). These include the meter, kilogram, and second. Astronomers also use many of their own units, including the astronomical unit, light year, and parsec, all of which are measures of distance. Astronomers find these units more convenient than the conventional SI units when describing the mind-boggling distances between astronomical objects. For example, Jupiter is about 7.8 x 10⁸ km from the Sun; we can also express this distance as 5.2 astronomical units (au). The astronomical unit is a convenient unit for describing distances inside our solar system; the average distance between the Sun and the Earth is 1 au. Light years and parsecs are convenient units for describing distances beyond our solar system or even outside of our galaxy, the Milky Way.

Scientific Notation

In astronomy (and other sciences), it is often necessary to deal with very large or very small numbers. In fact, when numbers become truly large in everyday life, such as the national debt in the United States, we call them astronomical. Among the measurements that astronomers routinely deal with is that the Earth is 150,000,000,000 meters from the Sun, and the mass of the hydrogen atom is 0.00000000000000000000000000167 kilograms. No one in his or her right mind would want to continue writing so many zeros!

Instead, scientists have agreed on a kind of shorthand notation, which is not only easier to write, but makes multiplication and division of large and small numbers much less difficult. If you have never used this powers-of-ten notation or scientific notation, it may take a bit of time to get used to it, but you will soon find it much easier than keeping track of all those zeros.

Powers of Ten

Scientific notation is a powers-of-ten notation. Our counting system is based on increases of ten; each place in our numbering system is ten times greater than the place to the right of it. There is the ones place, tens place, hundreds place, thousands place, etc… As you have probably learned, this got started because human beings have ten fingers and we started counting with them. (It is interesting to speculate that if we ever meet intelligent life-forms with only eight fingers, their counting system would probably be a powers-of-eight notation!)

When converting numbers to scientific notation, you’ll need to keep track of powers of ten. Ten (10) is one ten, which can also be written as 10¹. One hundred (100) is ten times ten, or two powers of ten, which we write as 10². A thousand is three powers of ten (10³), a million is six powers of ten (10⁶), and a billion is nine powers of ten (10⁹). The table below shows several powers of ten with their name, long form, and exponential form.

Ten	10	10¹
Hundred	100	10²
Thousand	1,000	10³
Million	1,000,000	10⁶
Billion	1,000,000,000	10⁹
Trillion	1,000,000,000,000	10¹²

This powers of ten notation continues into decimal places. We have the tenths place (1/10), the hundredths place (1/100), the thousandths place (1/1000), etc. Each place value to the right of the decimal point is smaller by a factor of ten. We keep track of these increasingly smaller place values using negative powers of ten. One tenth (1/10) is 10^-1; a hundredth (1/100) is 10^-2. You might be wondering what power to assign the simple number one; the answer is that one is 10⁰. This might seem odd, but it keeps the pattern of decreasing and increasing exponents across the place values.

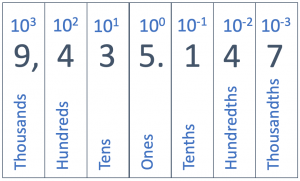
Figures showing the correspondence between place values and powers of ten. — Each place value (one, tens, hundreds, etc.) has a corresponding power of ten. Notice that the ones place is ten to the zeroth power.

Writing Large Numbers

In scientific notation, we generally agree to have only one (non-zero) number to the left of the decimal point. If a number is not in this format, it must be changed. The number 6 is already in the right format, because for integers, we understand there to be a decimal point to the right of them. So 6 is really 6., and there is indeed only one number to the left of the decimal point. But the number 965 (which we could write as 965.) has three numbers to the left of the decimal point, and needs to be converted to be in scientific notation.

To change 965 into scientific notation, we start by recognizing that 965 is 9.65 times 100. We write the 100 in exponent form, 10², and 965 becomes 9.65 × 10². The small raised 2 is called an exponent; it tells us how many times we need to multiply 9.65 times 10. We read 9.65 × 10² as “9.65 multiplied by ten to the second power”.

Put another way, the exponent on the power of ten indicates the place value of the leading digit. In the example, 9.65 × 10² , the exponent (2) lets you know that the 9 is in the hundreds place (10² is one hundred, see the table above). The rest of the number follows, 9.65 × 10² is 965. For another example, 4.256 x 10⁶ is 4.256 million (10⁶ is a million), which we can write out as 4,256,000.

The Power of ten tells you the place value of the leading digit. — The power of ten tells you the place value of the leading digit. In this case, six is the power of ten, so the leading digit, 4, goes in the millions place.

A shortcut that you can use when converting numbers into scientific notation is to count the number of place values that you need to move the the decimal to left (or to the right for numbers less than one) in order to have a single non-zero unit to the left of the decimal point (in the one’s place). In the example above, to convert 965 to 9.65, you must move the decimal point two places to the left. So 965 is 9.65 × 10², where the 2 tells us how many times we moved the decimal point to the left.

For another example, the number 1,372,568 becomes 1.372568 × 10⁶. We had to move the decimal point six places to the left (from its place after the 8) to get the number into the form where there is only one digit to the left of the decimal point. Each time we move the decimal point to the left, we must multiply by another power of ten.

To convert this number to scientific notation, the decimal point must move 6 places to the left. The power ten in scientific notation is 6.

In the example we started with, the number of meters from Earth to the Sun is 1.5 × 10¹¹ meters. For another example, a string 1 light-year long would fit around Earth’s equator 236 million or 236,000,000 times. In scientific notation, this would become 2.36 × 10⁸.

Writing Small Numbers

Now consider a number like 0.00347, which is also not in the standard (agreed-to) form for scientific notation. To be in scientific notation, a number must have a single non-zero digit to the left of the decimal point. This example is not in scientific notation because the number in the one’s place is a zero. To convert this number into scientific notation, start by rewriting it as 3.47 times 0.001. The number 0.001 is one thousandth, or 1 divided by 1000, which we write in exponential form as 10⁻³. In scientific notation, 0.00347 is 3.47 x 10^-3.

We can also use our shortcut to put 0.00347 into scientific notation. Make the first part of the number 3.47 by moving the decimal point three places to the right. Note that this motion to the right is the opposite of the motion to the left that we discussed above. When we move the decimal place to the right, the number is smaller than one, and the exponent on the ten is negative. In this example, 0.00347 becomes 3.47 × 10⁻³. (It is a common mistake when writing small numbers in scientific notation to count the zeros to the left of the decimal instead of counting how many place values to the left you must move the decimal. Notice that there are only two zeros after the decimal, but you must move the decimal point three places to the left to convert 0.00347 into scientific notation.)

To convert 0.00347 to number to scientific notation, the decimal point must move 3 places to the right. — To convert this number to scientific notation, the decimal point must move 3 places to the right. The power ten in scientific notation is -3.

In the example that we gave at the beginning, the mass of the hydrogen atom would then be written as 1.67 × 10⁻²⁷ kg. Note that any number, no matter how large or how small, can be expressed in scientific notation.

If this is the first time that you have met scientific notation, we urge you to practice many examples using it. Like any new language, the notation looks complicated at first but gets easier as you practice it.

SI Units

Scientists across the different disciplines — physics, chemistry, biology, astronomy, geology, etc. — all use a single set of units, call the metric International System of Units or SI units. This system not only establishes a set of units (the meter, second, kilogram, etc.), but defines what each of these units means. The definitions of these units have changed over time, becoming more precise as technology has improved. For example, the original definition of a second was 1/86400 of a day. (A typical day has 24 hours, with 60 minutes in each hour, and 60 seconds in each minute, for a total of 86400 seconds per day.) The current definition of the second is based on cesium atomic clocks; the “unperturbed ground-state hyperfine transition frequency of the cesium 133 atom” is defined “to be 9 192 631 770 when expressed in the unit Hz, which is equal to s^-1.”^[1] Both of these definitions are very close to each other, but the current definition allows for more precise timekeeping, which many modern technologies rely on.

In the American system of measurement (originally developed in England), the fundamental units of length, weight, and time are the foot, pound, and second, respectively. There are also larger and smaller units, which include the ton (2240 lb), the mile (5280 ft), the yard (3 ft), the inch (1/12 ft), the ounce (1/16 lb), and so on. These units can be convenient in many practical contexts (it’s easier to make a half or a third or a recipe in British Imperial units than in metric units), but they are inconvenient when converting units and doing calculations. ^[2]

In science, it is more usual to use the metric system, which has been adopted in virtually all countries except the United States. The fundamental units of the metric system are:

length: 1 meter (m)
mass: 1 kilogram (kg)
time: 1 second (s)

These units were adopted as part of the SI system of units. ^[3] A meter is about 1.1 yd. A kilogram is the mass that on Earth results in a weight of about 2.2 lb. The second is the same in metric and American units.

The advantage of the metric system is that is built around factors of ten, just like our system of counting and writing numbers. The metric system includes a set of prefixes that indicate how many powers of ten the base unit has been multiplied by. For example, the prefix kilo means 1000 (10³); a kilometer (km) is 1000 meters (m). The prefix centi means a hundredth (10^-2); a centimeter (cm) is one hundredth (0.01) of a meter (m). The table below gives the most common prefixes.

Prefix	Symbol	Factor (Powers of 10)
fempto	f	10^-15
pico	p	10^-12
nano	n	10^-9
micro	μ	10^-6
milli	m	10^-3
centi	c	10^-2
deci	d	10^-1
kilo	k	10³
mega	M	10⁶
giga	G	10⁹
tera	T	10¹²

It is fairly straightforward to move between measurements written using these prefixes and scientific notation. For example, 3 km is 3 x 10³ m, 1.25 μg is 1.25 x 10^-6g, and 3.2 ms is 3.2 x 10^-3 s. You might sometimes have to take an extra step when rewriting a measurement. For example, 25 km is 25 x 10³ m, but this is not yet in scientific notation. To finish, move the decimal one place to the left and write 2.5 x 10⁴m.

In addition to the SI units, scientists in the individual disciplines also use units that are helpful within their fields. Astronomers use astronomical units, light years, parsecs, and solar masses. While most physics and chemistry textbooks primarily use SI units, you’ll also see atomic mass units (a unit of mass used for single atoms) and electron-volts (a very small, but useful, unit of energy) among other discipline-specific units. Theoretical physicists often prefer a system of units in which the speed of light is 1 (in SI units it’s 2.99792458 x 10⁸ m/s).

Multiplying and Dividing with Very Large or Very Small Numbers

Scientists don’t only measure things that are very small or very large, they perform calculations with these measurements. Scientific notation is not only a convenient way to write numbers, it also simplifies these calculations.

Some of the simplest examples of performing arithmetic with scientific notation involve making comparisons. For example, the radius of a single hydrogen atom is 52.9 pm (picometers). The radius of the Earth is 6,370 km. We might ask, how many times larger is the radius of the Earth than the radius of a hydrogen atom? The fastest and easiest way to find the answer is by multiplying and dividing using scientific notation.

Multiplication

To multiply two numbers expressed in scientific notation, you first multiply the numbers out front and then add the exponents on the tens. If there are no numbers out in front, for example, 10² × 10⁵ , then simply add exponents to find the answer; 10² × 10⁵ = 10⁷. When there are numbers out front, you have to multiply them, but they are much easier to deal with than numbers with many zeros in them.

Here’s an example:

$\left(3\times {10}^{5}\right)\times \left(2\times {10}^{9}\right)=6\times {10}^{14}$

And here’s another example:

$\begin{array}{cc}\hfill 0.04\times 6,000,000& =\left(4\times {10}^{-2}\right)\times \left(6\times {10}^{6}\right)\hfill \\ & =24\times {10}^{4}\hfill \\ & =2.4\times {10}^{5}\hfill \end{array}$

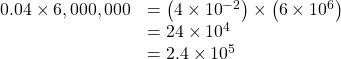
Note in the second example that when we added the exponents, we treated negative exponents as we do in regular arithmetic (−2 plus 6 equals 4). Also, notice that our first result had a 24 in it, which was not in the acceptable form, having two places to the left of the decimal point, and we therefore changed it to 2.4 and changed the exponent accordingly.

We can use these rules for multiplying exponents to quickly convert between units in the metric system. For example, 1.3 km is 1.3 x 10⁵ cm. There are 10³ meters in a km and 10² cm in each of those meters. Multiplying, there are 10³ x 10² = 10⁵ cm in each kilometer^[4]; so, 1.3 km is 1.3 x 10⁵ cm. We can also convert from a smaller unit (e.g., grams) to a larger unit (e.g., kilograms, a kilogram is larger than a gram). For example, 100 g is 0.1 kg. There are 10³ g in each kg; so each gram is only one thousandth (10^-3) of a kilogram. If we have 100 (or 10²) grams, then we can multiply by 10^-3 to find that this is equivalent to 10² x 10^-3 = 10^-1 kilograms, or 0.1 kg.

To help with our example from above, let’s convert both the radius of the Earth and the radius of a hydrogen atom into meters, being sure to express both in scientific notation. The radius of the Earth is 6,370 km, or 6,370 x 10³ m. Written in scientific notation, this is 6.37 x 10⁶ m. The radius of a hydrogen atom is 52.9 pm, or 52.9 x 10^-12 m, which we write in scientific notation as 5.29 x 10^-11 m.

Division

To divide using scientific notation, you divide the numbers out front and subtract the exponents. Here are several examples:

$\begin{array}{ccc}\hfill \frac{1,000,000}{1000}& =\hfill & \frac{{10}^{6}}{{10}^{3}}={10}^{\left(6 - 3\right)}={10}^{3}\hfill \\ \hfill \frac{9\times {10}^{12}}{2\times {10}^{3}}& =\hfill & 4.5\times {10}^{9}\hfill \\ \hfill \frac{2.8\times {10}^{2}}{6.2\times {10}^{5}}& =\hfill & 0.452\times {10}^{\text{-}3}=4.52\times {10}^{-4}\hfill \end{array}$

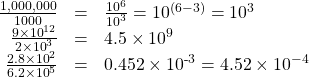
In the last example, our first result was not in the standard form, so we had to change 0.452 into 4.52, and change the exponent accordingly.

To find out how much larger the radius of the Earth is than the radius of a hydrogen atom, divide the radius of the Earth (6.37 x 10⁶ m) by the radius of a hydrogen atom (5.29 x 10^-11 m) (and remember that subtracting a negative number is that same as adding a positive number).

(1) $\begin{equation*}\frac{6.37\times {10}^{6} \rm{m}}{5.29\times {10}^{-11} \rm{m}}=1.2\times {10}^{17}\end{equation*}$

The radius of the Earth is 1.2 x 10¹⁷, or 1.2 x 10⁵ trillion, times larger than the radius of a hydrogen atom.

Attributions

This chapter is adapted from Chapter 1, Science and the Universe: A Brief Tour and Appendix C: Scientific Notation from Astronomy by A. Fraknoi and D. Morrison, the current version of which is available through OpenStax. OpenStax is licensed under Creative Commons Attribution License v4.0.

NIST -- The National Institute of Standards and Technology -- lists the definitions of the SI Base Units at https://www.nist.gov/si-redefinition/definitions-si-base-units ↵
The Imperial system of units is built primarily around factors of two and three. There are two cups in a pint, eight tablespoons (2³) in a cup, 3 teaspoons in a tablespoon. Similarly, there are three feet in a yard and a third of a foot is simple 4 inches. This makes is easy to work in thirds and halves, which can be very practical, but you can't convert between units by moving the decimal. In the metric system, 1 cm is a hundredth of a meter (0.01 m), but an inch is 0.2777... of a yard. ↵
A meter was originally intended to be 1 ten-millionth of the distance from the equator to the North Pole along the surface of Earth. The meter is defined by defining the speed of light in a vacuum to be 299 792 458 m/s, where the second is defined using a cesium atomic clock, as mentioned previously. ↵
This calculation can be written as 10³ m/km x 10² cm/m = 10⁵ cm/km ↵

License

Icon for the Creative Commons Attribution-NonCommercial 4.0 International License