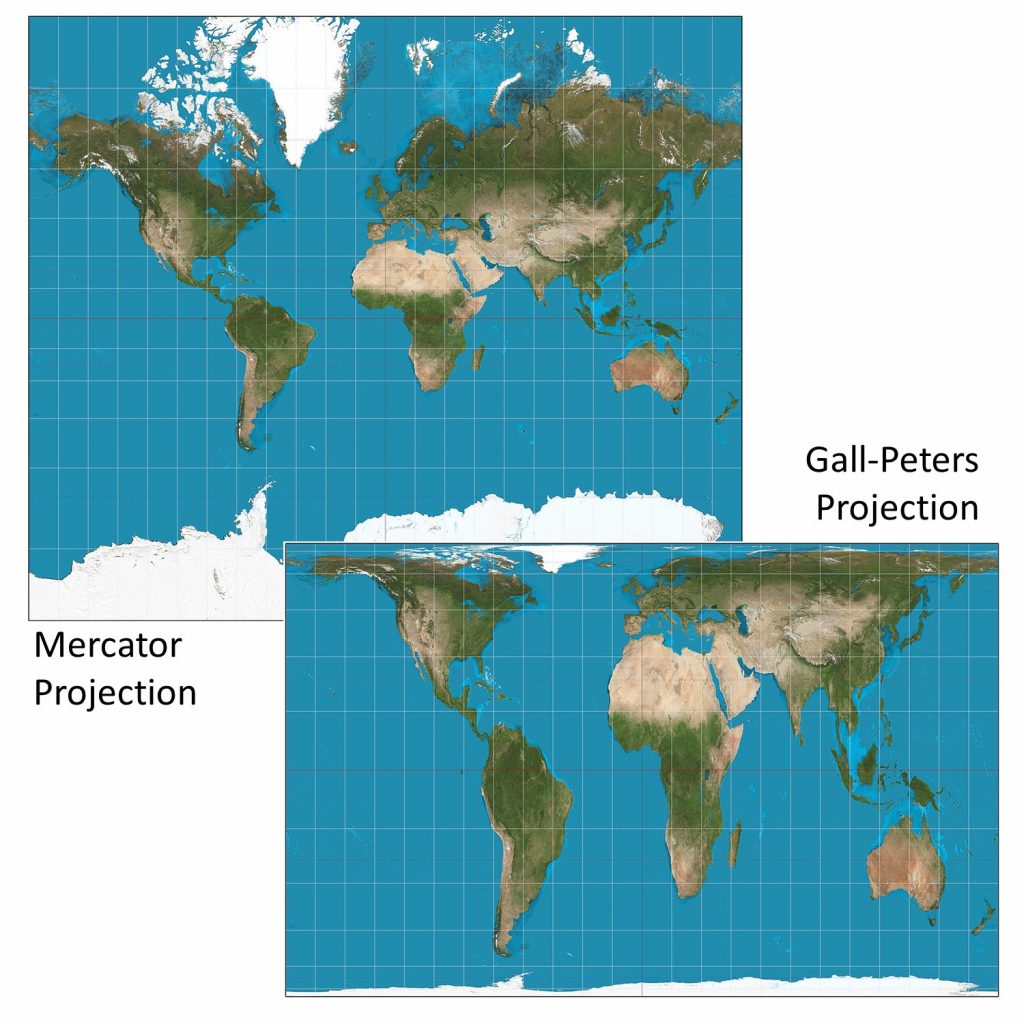
5.1 Little lies

Cartograms are another way of lying with symbolization. Cartograms are maps that distort area or distance by substituting another thematic variable. Because of the dramatic distortions that cartograms produce, you might consider them to be telling more than white lies. However, cartograms are just different ways of symbolizing the same data in order to tell a story. The big lies that we discuss in the next section are lies that are told for very specific purposes or for eliciting particular reactions. Cartograms are considered white lies here because they are just another set of symbolization choices that affect the representation of data on your map.

The figure below is an example of a map showing the number of people and the amount of wealth per country in 2015. Note how the size of any given country is not displayed in accordance with the land mass of that country, but in fact, corresponds to the number of people living there or its total wealth. This map gives you, very quickly and effectively, a read on which countries have the most people and most money.

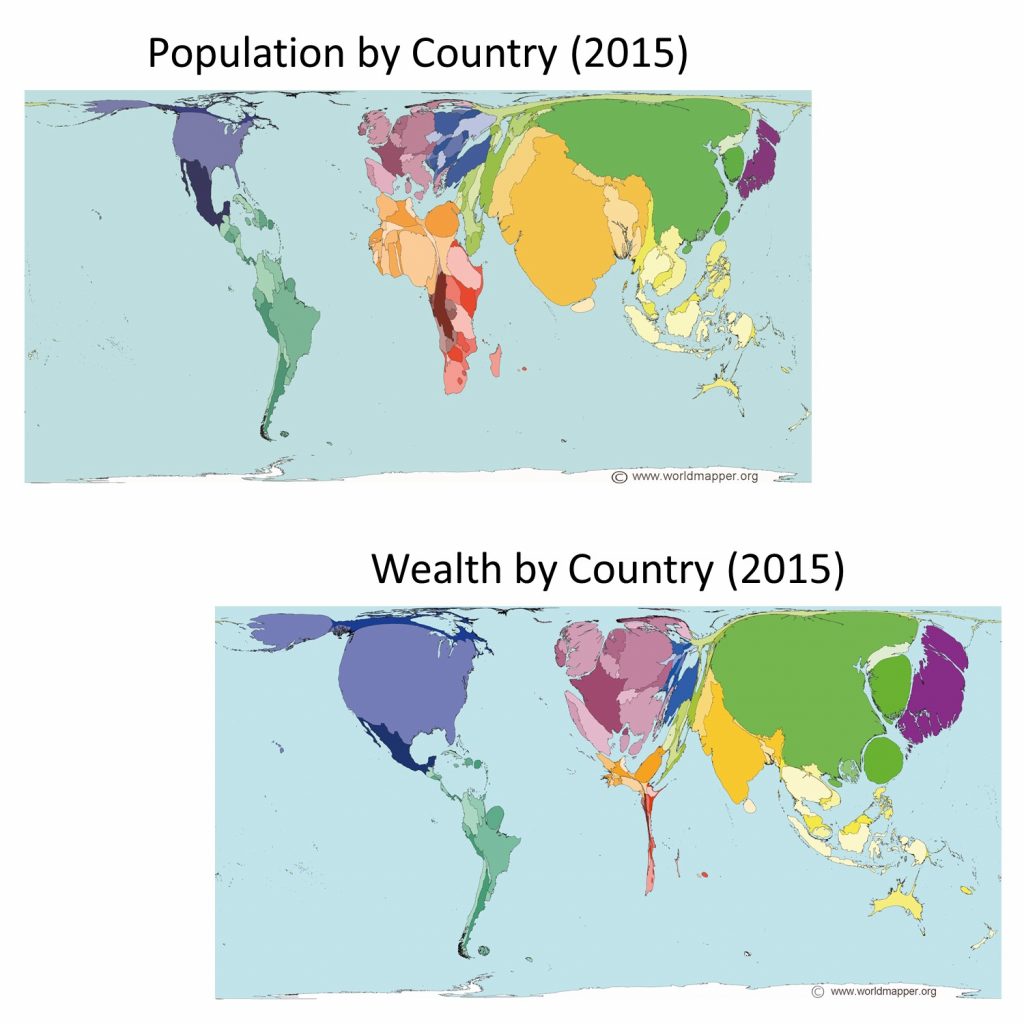
Lying with cartograms. Population total and wealth by country in 2015. Note how the size of countries on the map is not their actual area but instead proportional to the attribute being measured, population or wealth. ^[3]

5.1.3 Standardization

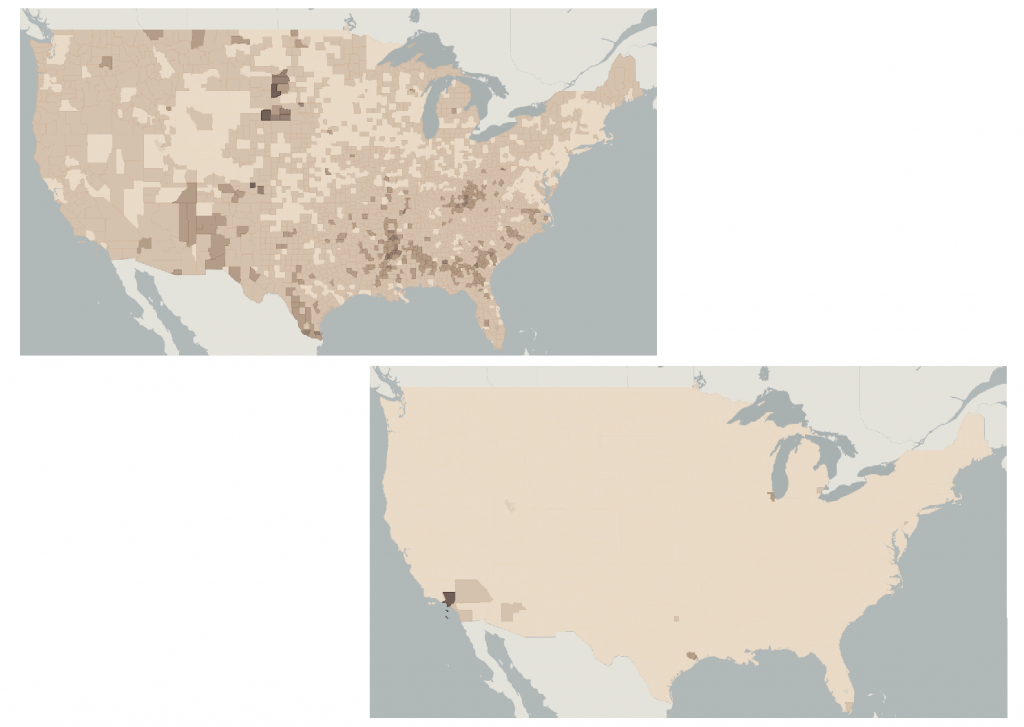
How and whether data is standardized (standardization) also has a huge impact on the story that the map tells. The maps in the figure below represent poverty data from the 2000 US census. The top map standardizes data by the percentage of the population – the number of people living in poverty relative to the total population of that census tract. The bottom map is based on raw numbers for how many people are living in poverty in the census tract. By failing to account for poverty as a percentage of the total population, the bottom map tells a much bigger lie about poverty levels in the US.

Lying with standardization. Poverty as a percentage versus poverty as a raw number. These maps represent poverty data from the 2000 US Census but differ in their standardization. ^[4]

5.1.4 Classification

Classification matters. Choices you make about how to classify your data can have a big impact on the story that your map tells. The maps here show how you can lie with classification. The three maps in the figure below each use the same data, the same number of classes, the same color scheme, and the same standardization, yet each tells a very different story about poverty in the US, depending upon the classification scheme. The first map classifies the data using equal interval, the second using natural breaks, and the third using a quantile scheme.

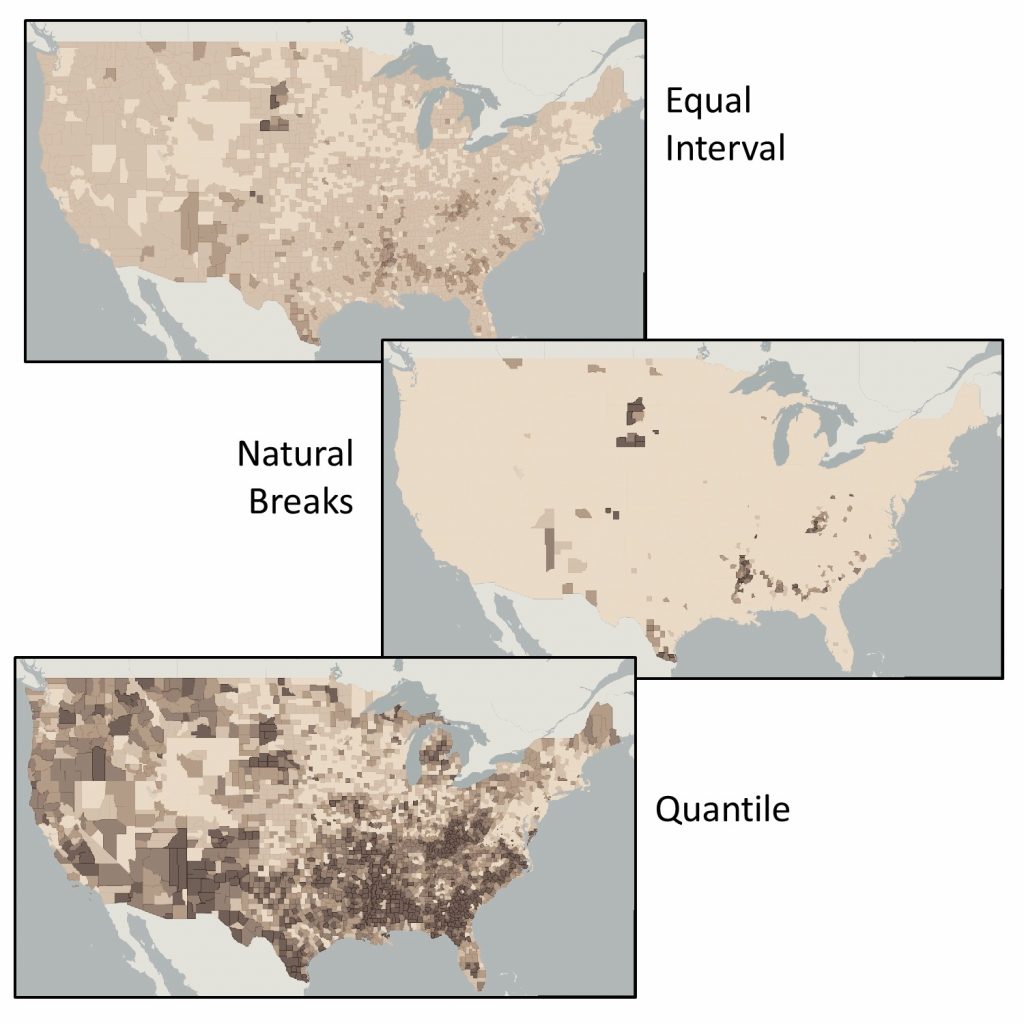
Lying with classification. Poverty via equal interval, natural breaks, and quantile classifications. The three maps use the
same data, the same number of classes, the same color scheme, and standardization, yet each tells a very different story about poverty in the US. ^[5]

The figure below shows three maps of 2000 census poverty data. Each uses a quantile classification scheme. The only difference is the number of classes. See how the number of classes impacts your perception of poverty levels in the US. Although there are some areas that demonstrate patterns of poverty across the three maps, as you increase the number of classes, you get a more nuanced picture of how poverty is distributed across the country.

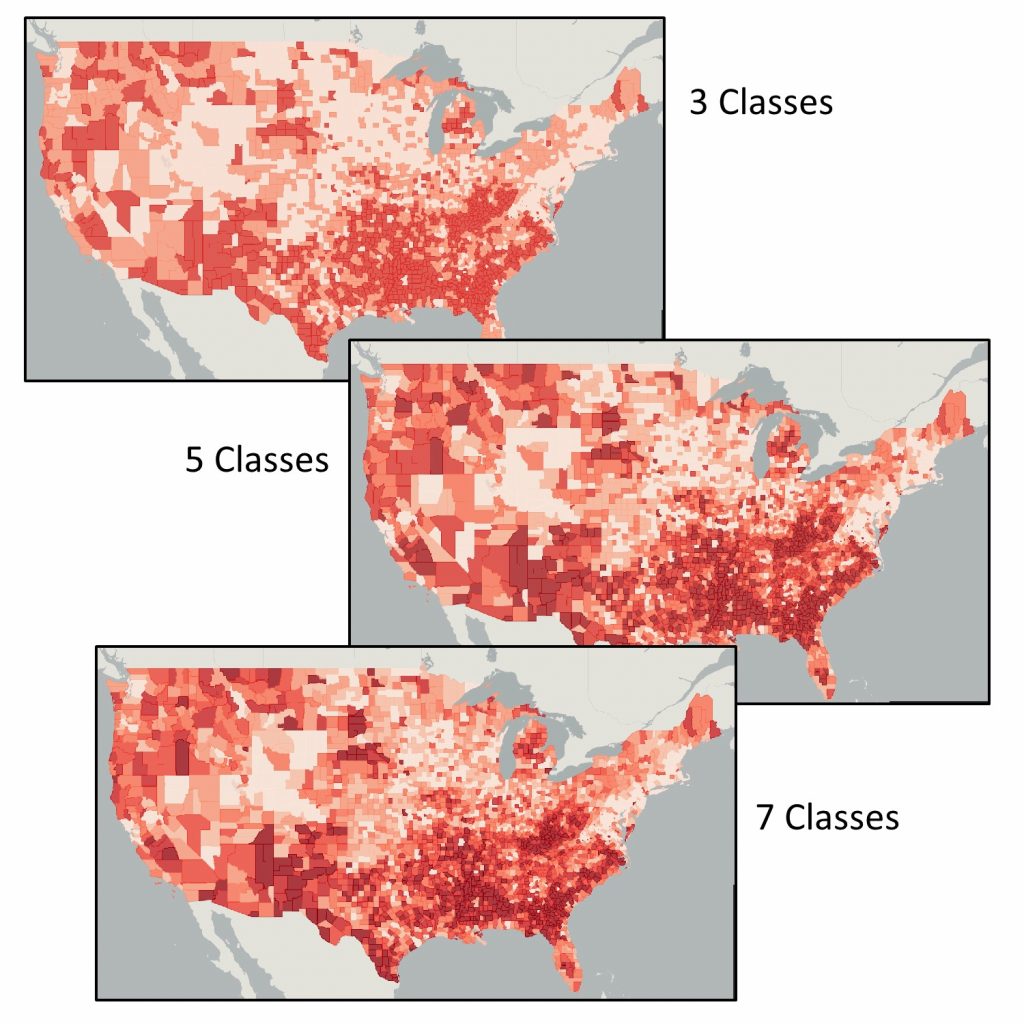
Lying with classes. Poverty via quantile classifications with a differing number of classes. The three maps use the same data and color scheme yet tell a different story about poverty in the US. ^[6]

5.1.5 Aggregation, Classification, and the Ecological fallacy

Recall that data are often aggregated. They are often collected at one scale, such as the household or neighborhood, and then reported at much broader scales, such as the census tract or county. This is termed aggregating the data. While aggregation can be very helpful in terms of preserving privacy or presenting a broader and synoptic view, it can also lead to the ecological fallacy, or the assumption that a characteristic or value calculated for a group in aggregate can be applied to an individual member of that group. In other words, aggregated data makes it hard to assume or guess at the characteristics of any given individual found in that aggregated area.

Imagine you are comparing the income of two blocks, each being composed of five households. Block A has an average household income of $48,000 while Block B has an average household income of $40,000, per the figure below. In which area are you more likely to find a household with a higher income? If you chose Block A—the area with the higher average income total—then you were tricked by the ecological fallacy. In fact, there is no way to know from aggregated data alone what the situation is like for an individual within a group. The figure shows one of many possible scenarios under which four out of five households in Block B have higher incomes than households in Block A.

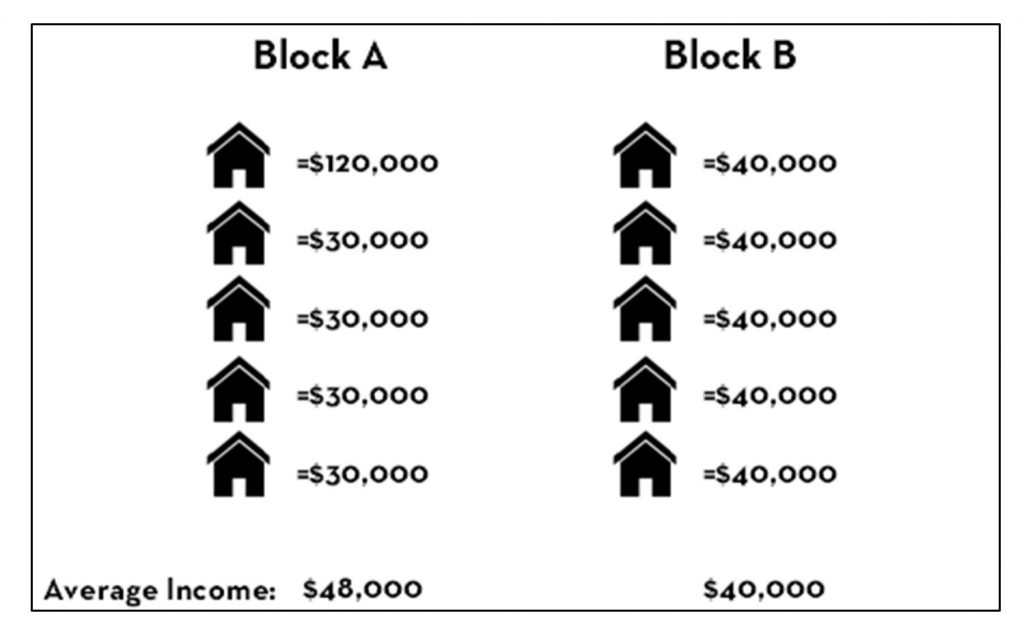
Ecological fallacy. Consider this scenario in which Block A has a higher aggregated average income but mostly lower individual values than Block B. ^[7]

Watch out for the ecological fallacy whenever you are interpreting maps, or you might come to false conclusions about the people who live in a neighborhood or other areas!

The danger of the ecological fallacy for the map reader is closely tied to the subtle ways that mapmakers can lie with aggregation, often in combination with classification. The figure below illustrates voting returns for the 2012 US presidential election. The map on the left represents counties by their majority vote in the election. Red signifies counties where a majority of residents voted for the Republican candidate, Mitt Romney; blue signifies counties with a majority vote for the Democratic candidate Barack Obama. The map on the right attempts to reveal a little more nuance in voting patterns, by using a red-purple—blue scale to indicate percentages of votes, while the one on the left is simpler and more prone to the ecological fallacy. These maps are both entirely correct. They differ in how they classify their underlying data into either two categories or by not classifying the data and instead of using hue and value to represent fine differences among counties.

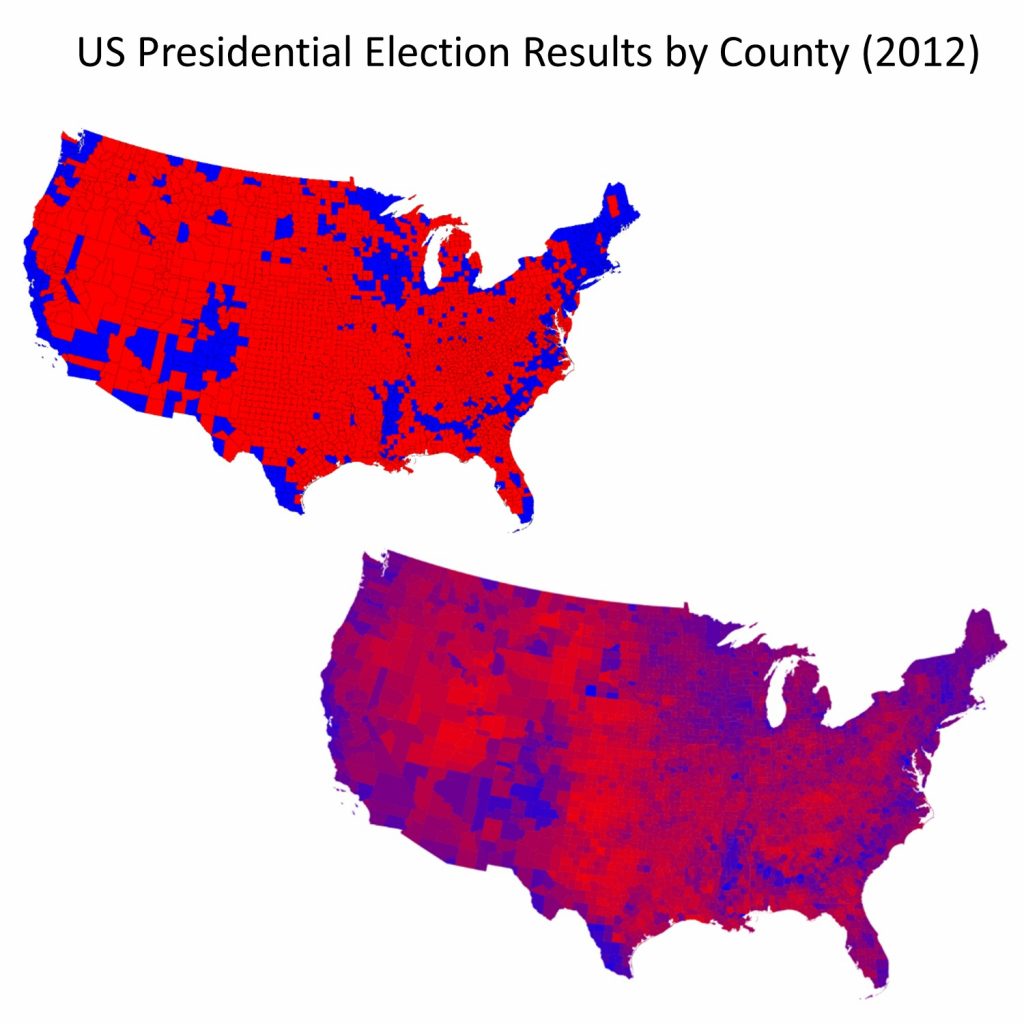
Lying with aggregation and classification. Lying, or rather telling different truths, about the United States presidential election in 2012. The map on the left shows counties by their majority vote in the election, where red means counties where a majority of residents voted for the Republican candidate and blue signifies counties voting Democrat. ^[8]

From your knowledge of the ecological fallacy, you know that even at the level of the county, this map does not accurately represent the party affiliation, beliefs, or voting patterns of each person in the county. The data are aggregated to the county level and are classified differently than the data in the map on the right. This sort of aggregation and classification is useful because it allows us to distinguish between voting patterns in different parts of the country—rural/urban variations, for instance. The map on the right is still lying of course—not all residents in the US voted, and those who did were not necessarily voting for the endorsed Republican or Democratic candidate—but it is trying to provide a more accurate picture of the data. Both maps lie in order to give a picture of the election outcome in particular parts of the country.

Consider the cartogram version of the election map, below. The cartogram distorts area based on county-level election returns, so counties with larger populations appear bigger. The cartogram lies by distorting area, but in some ways, it gives us a clearer picture of election results. In the standard county aggregation map above it appears that the US voted strongly Republican; but the cartogram shows that many Republican-leaning counties have relatively small populations, while counties with larger populations mainly voted for the Democratic candidate.

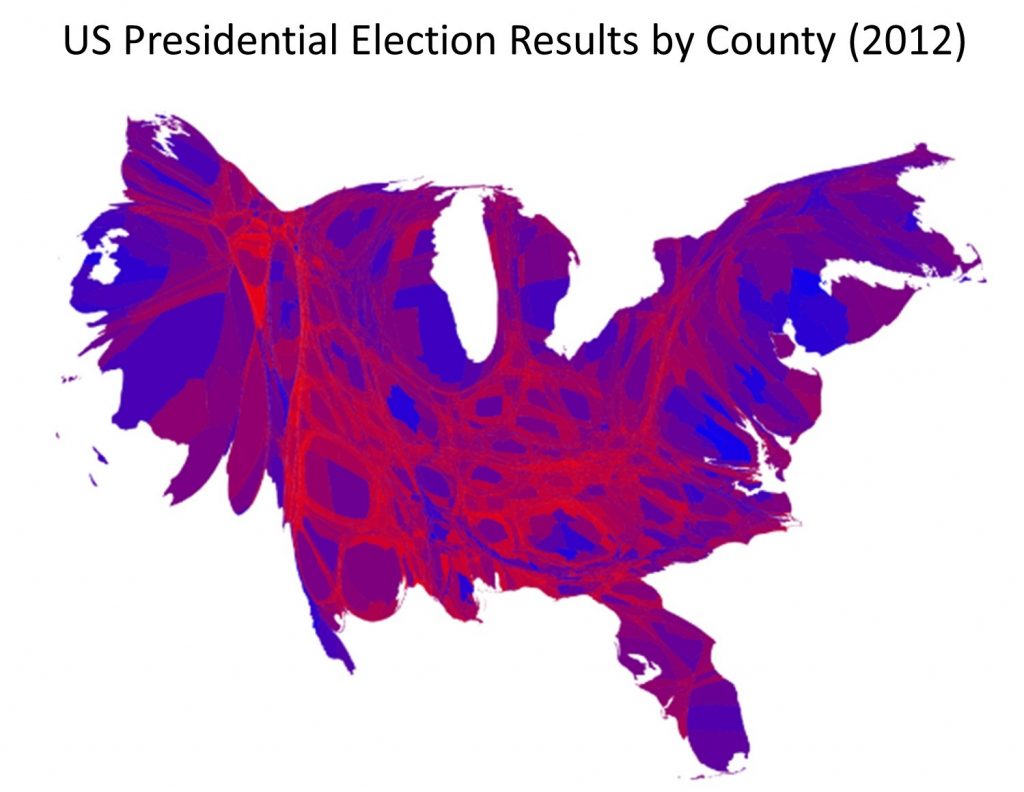
Election cartogram. This cartogram of election results distorts apparent county area by the number of returns, so counties with larger populations appear bigger. ^[9]

5.1.6 Aggregation and Zonation

We have looked at how data are aggregated to larger areas and how this process of aggregation can affect how data are interpreted, such as causing the potential for the ecological fallacy. In addition to aggregating data, we can also zone it differently, which is another way of saying we can draw an almost infinite array of differing boundaries for any given aggregation. We often use county boundaries in our analyses, for example, but the boundaries of counties are arbitrary. They were drawn over time according to a range of different principles, such as where a river flowed or where settlement was being encouraged. Population data is often aggregated and reported by county but they could be (and often are) reported via other zonations, such as zip codes, phone-number area codes, school districts, or watershed boundaries.

Importantly, the way in which data are aggregated and where the boundaries of zones are drawn can easily change data patterns and analysis outcomes. Depending on the scale at which you look at a geographic pattern, you can derive completely different results from the exact same underlying data. This is called the modifiable areal unit problem. For example, consider the rate of a disease in a population. Individuals at specific locations become sick, but health officials often want to know the broader trends of diseases. For this reason – and to protect the privacy of patients – they may count the number of cases by block, zip code, or another zonation. But artificially breaking up space into these larger areas can change the apparent patterns of disease. The figure below illustrates this for deaths from respiratory problems in Ottawa, Canada. Each map uses the same underlying data but groups or zones cases differently: by a health department aggregation, by neighborhood, and by census tract. Each classes spatial units into quartiles, or in other words, divides the areas into four equal groups by how many people are dying in those areas. Note that these three maps all use the same exact underlying data and are just using different ways of zoning the groups. Nonetheless, these maps look very different, highlighting the challenge of the modifiable areal unit problem.

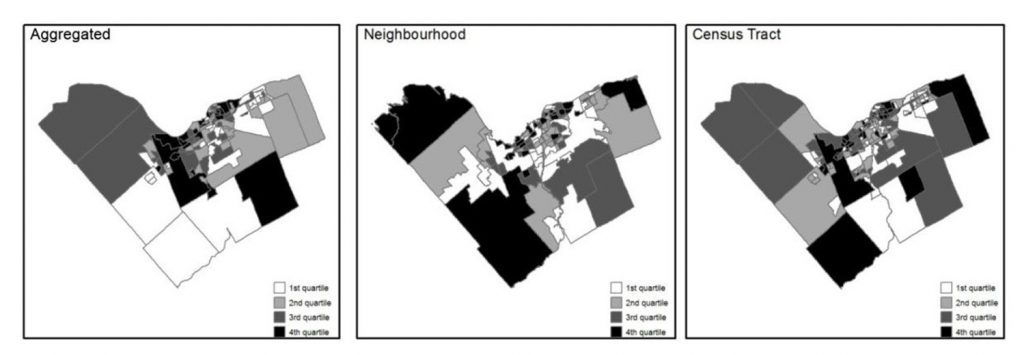
Health and zonation. These maps all show data on where people die from respiratory problems in Ottawa, Canada. Each map uses the same underlying data but groups or zones cases differently. Each categorizes spatial units into quartiles. ^[10]

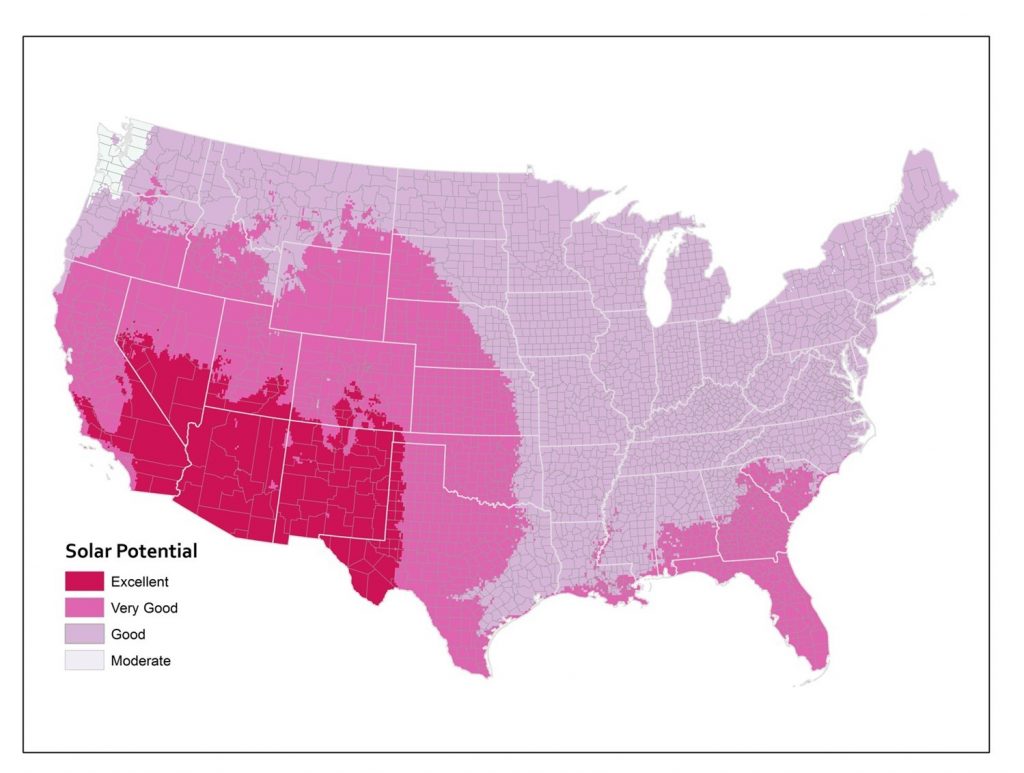
In addition to zoning, the modifiable areal unit problem can result from aggregation. Consider the figures below of solar potential in the lower 48 United States. Solar potential refers to the suitability of a particular place to develop solar power. These data are from the National Renewable Energy Laboratory and these maps were created by Anthony Robinson (2010). The first map shows the average annual solar potential by state. In other words, these data are aggregated by state. You can see right away that some states look better than others.

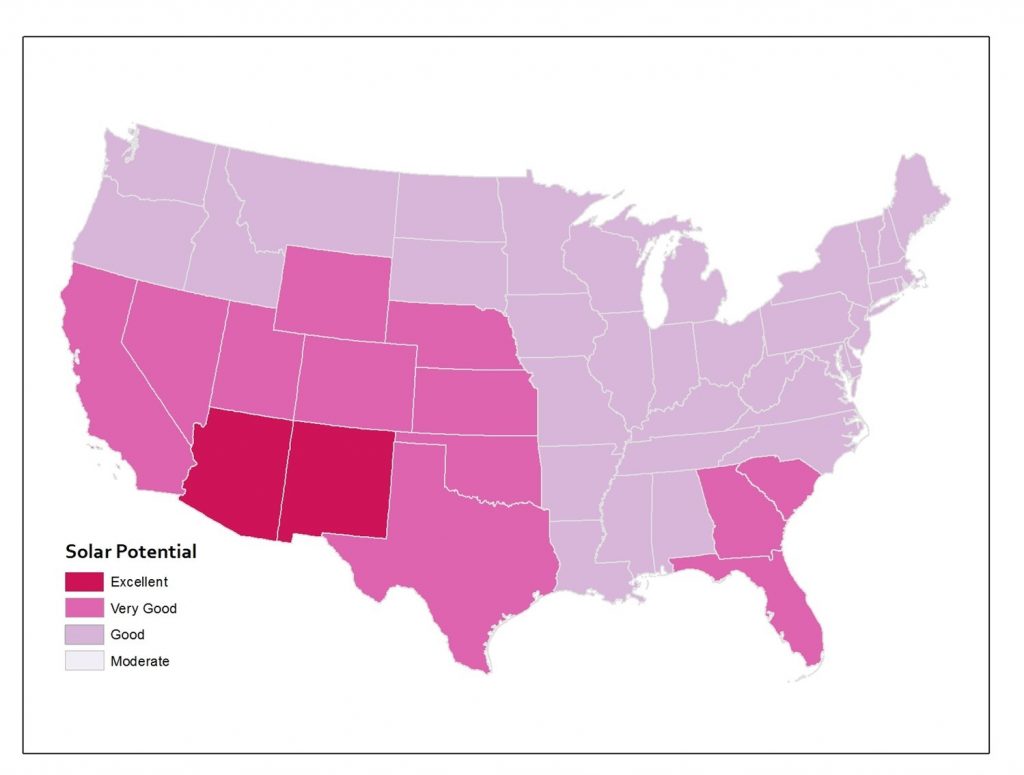
Solar potential by state. Annual solar potential by state, which measures the suitability of a particular place to develop solar power. ^[11]

The same underlying data aggregated to counties instead makes it look like a lot of states that were shown in one color at the state level actually include several categories of solar potential when you look at the data by county.

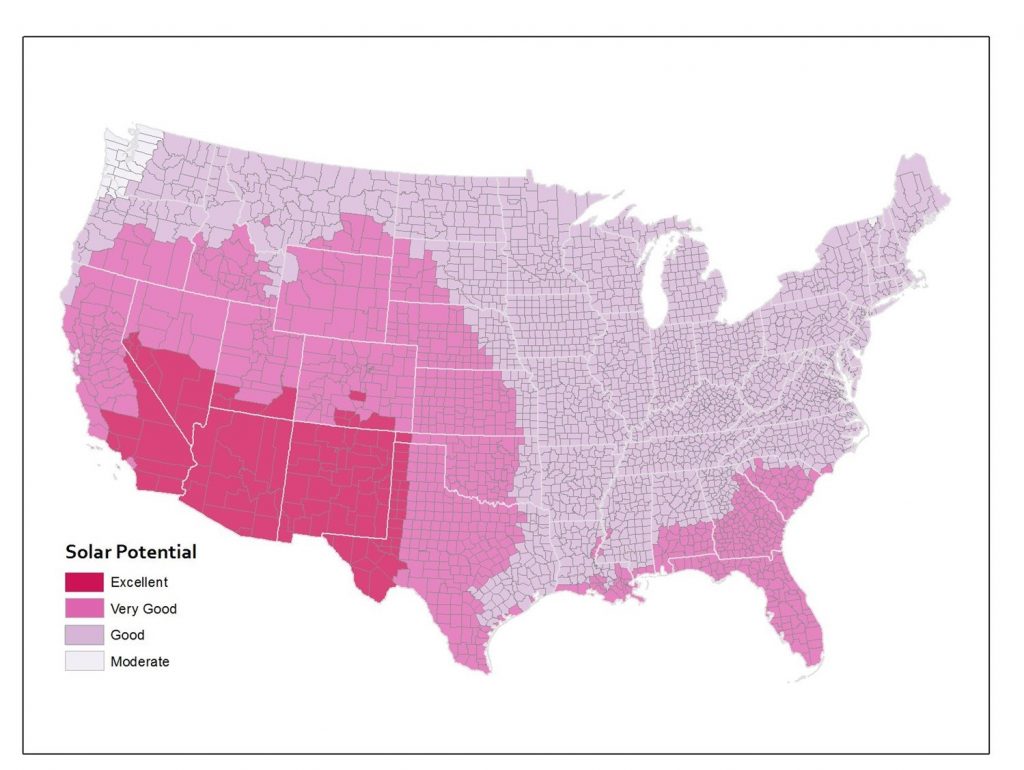
Solar potential by county. Annual solar potential by county, which measures the suitability of a particular place to develop solar power. ^[12]

The third map shows the original underlying data on which the other two maps were based. These original data calculate solar potential in 10-kilometer grid cells. You can see how the state and county boundaries compare to the raw data and how aggregation changes the apparent distribution of phenomena.

Solar potential by grid cell. Annual solar potential given by the original data, which used a 10km grid cell. ^[13]