6.1 Vector Data Models
In contrast to the raster data model is the vector data model. In this model, space is not quantized into discrete grid cells like the raster model. Vector data models use points and their associated X, Y coordinate pairs to represent the vertices of spatial features, much as if they were being drawn on a map by hand. The data attributes of these features are then stored in a separate database management system. The spatial information and the attribute information for these models are linked via a simple identification number that is given to each feature on a map.
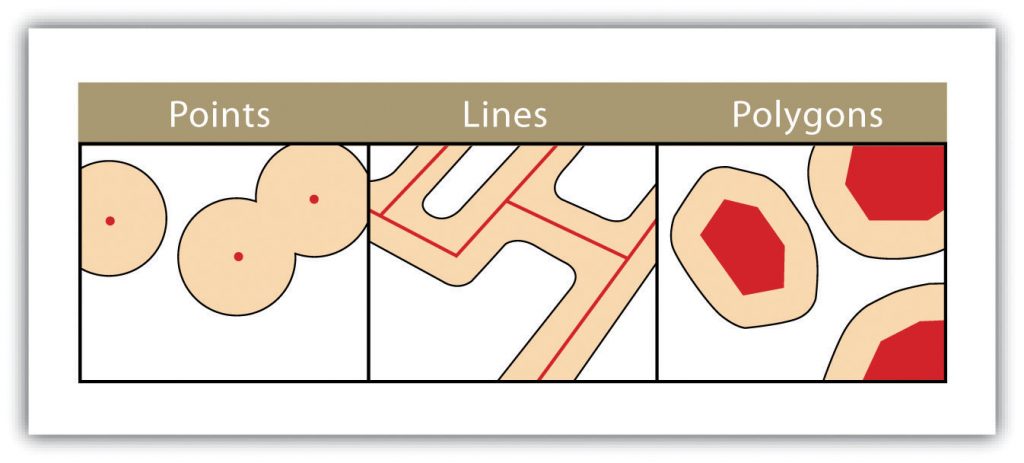
Three fundamental vector types exist in geographic information systems (GIS): points, lines, and polygons. Points are zero-dimensional objects that contain only a single coordinate pair. Points are typically used to model singular, discrete features such as buildings, wells, power poles, sample locations. Points have only the property of location. Other types of point features include the node and the vertex. Specifically, a point is a stand-alone feature, while a node is a topological junction representing a common X, Y coordinate pair between intersecting lines and/or polygons. Vertices are defined as each bend along a line or polygon feature that is not the intersection of lines or polygons.
Points can be spatially linked to form more complex features. Lines are one-dimensional features composed of multiple, explicitly connected points. Lines are used to represent linear features such as roads, streams, faults, boundaries. Lines have the property of length. Lines that directly connect two nodes are sometimes referred to as chains, edges, segments, or arcs.
Polygons are two-dimensional features created by multiple lines that loop back to create a “closed” feature. In the case of polygons, the first coordinate pair (point) on the first line segment is the same as the last coordinate pair on the last line segment. Polygons are used to represent features such as city boundaries, geologic formations, lakes, soil associations, vegetation communities. Polygons have the properties of area and perimeter. Polygons are also called areas.
Vector Data Models Structures
Vector data models can be structured in many different ways. We will examine two of the more common data structures here. The simplest vector data structure is called the spaghetti data model. In the spaghetti model, each point, line, and/or polygon feature is represented as a string of X, Y coordinate pairs (or as a single X, Y coordinate pair in the case of a vector image with a single point) with no inherent structure. One could envision each line in this model to be a single strand of spaghetti that is formed into complex shapes by the addition of more and more strands of spaghetti. It is notable that in this model, any polygons that lie adjacent to each other must be made up of their lines, or strands of spaghetti. In other words, each polygon must be uniquely defined by its own set of X, Y coordinate pairs, even if the adjacent polygons share the same boundary information. This creates some redundancies within the data model and therefore reduces efficiency.
Despite the location designations associated with each line, or strand of spaghetti, spatial relationships are not explicitly encoded within the spaghetti model; instead, they are implied by their location. This results in a lack of topological information, which is problematic if the user attempts to make measurements or analyses. The computational requirements, therefore, are very steep if any advanced analytical techniques are employed on vector files structured this way. Nevertheless, the simple structure of the spaghetti data model allows for efficient reproduction of maps and graphics as this topological information is unnecessary for plotting and printing.
In contrast to the spaghetti data model, the topological data model is characterized by the inclusion of topological information within the dataset. Topology is a set of rules that model the relationships between neighboring points, lines, and polygons and determines how they share geometry. For example, consider two adjacent polygons. In the spaghetti model, the shared boundary of two neighboring polygons is defined as two separate, identical lines. The inclusion of topology into the data model allows for a single line to represent this shared boundary with an explicit reference to denote which side of the line belongs with which polygon. Topology is also concerned with preserving spatial properties when the forms are bent, stretched, or placed under similar geometric transformations, which allows for more efficient projection and reprojection of map files.
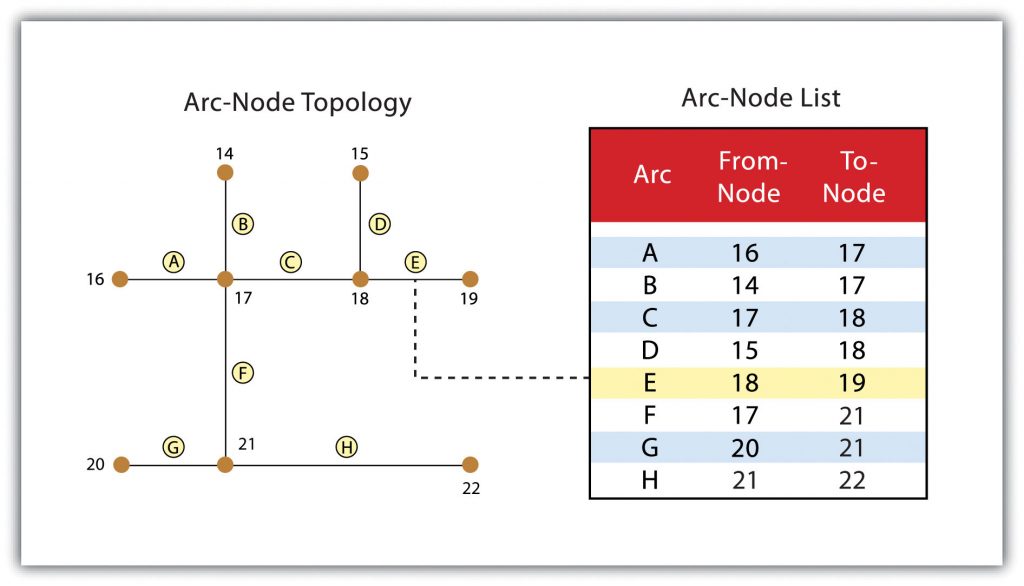
Three basic topological precepts that are necessary to understand the topological data model are outlined here. First, connectivity describes the arc-node topology for the feature dataset. As discussed previously, nodes are more than simple points. In the topological data model, nodes are the intersection points where two or more arcs meet. In the case of arc-node topology, arcs have both a from-node (i.e., starting node) indicating where the arc begins and a to-node (i.e., ending node) indicating where the arc ends. Also, between each node pair is a line segment, sometimes called a link, which has its identification number and references both its from-node and to-node. In Figure 6.1: “Arc-Node Topology,” arcs 1, 2, and 3 all intersect because they share node 11. Therefore, the computer can determine that it is possible to move along arc 1 and turn onto arc 3, while it is not possible to move from arc 1 to arc 5, as they do not share a common node.
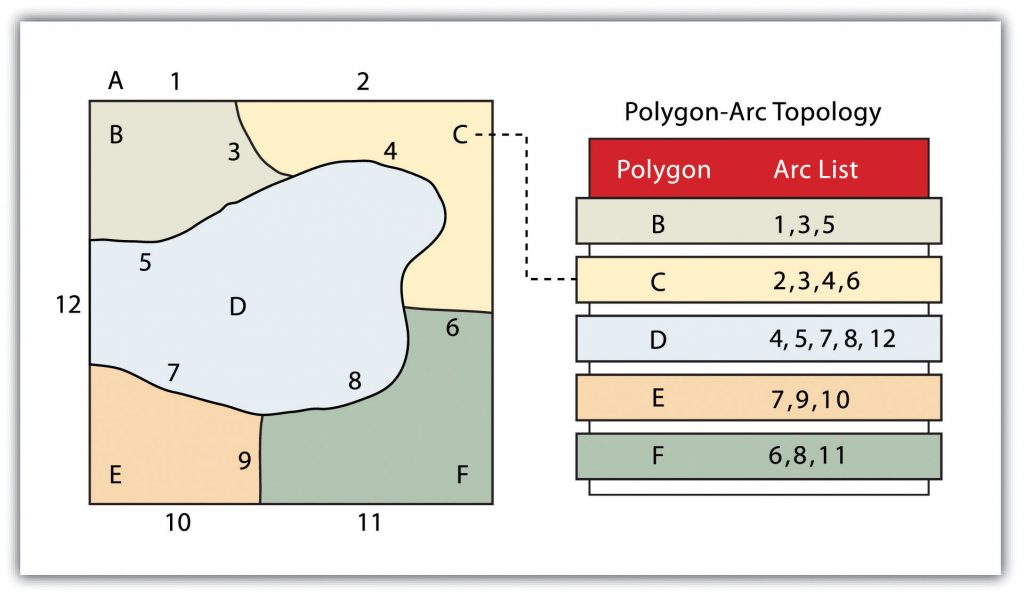
The second fundamental topological precept is area definition. Area definition states that an arc that connects to surround an area defines a polygon, also called polygon-arc topology. In the case of polygon-arc topology, arcs are used to construct polygons, and each arc is stored only once. This results in a reduction in the amount of data stored and ensures that adjacent polygon boundaries do not overlap. In Figure 6.2: “Polygon-Arc Topology,” the polygon-arc topology makes it clear that polygon F is made up of arcs 8, 9, and 10.
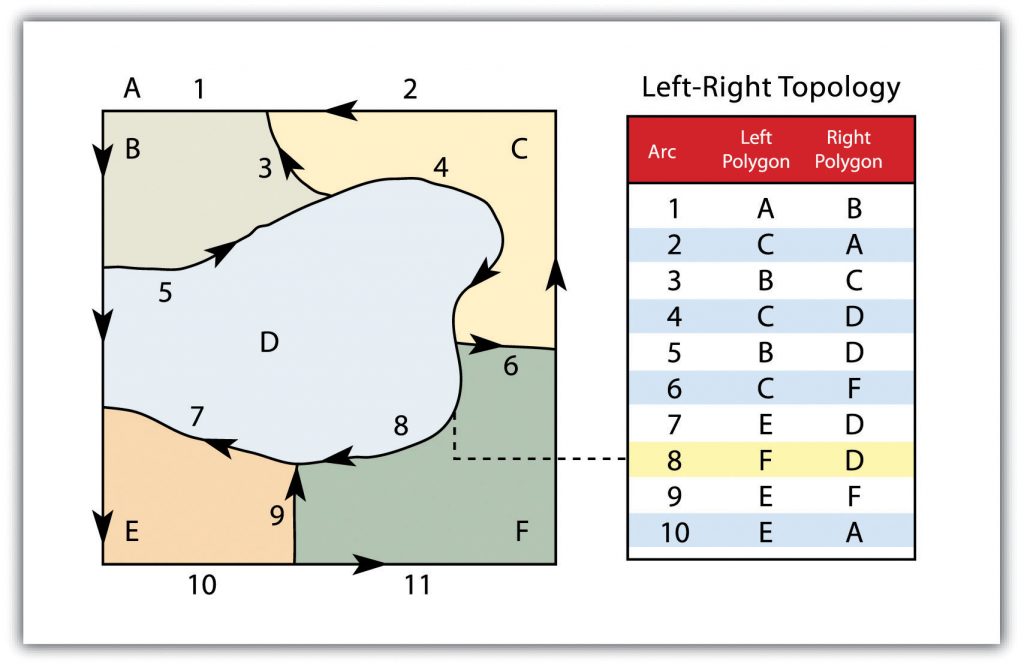
Contiguity, the third topological precept, is based on the concept that polygons that share a boundary are deemed adjacent. Specifically, polygon topology requires that all arcs in a polygon have a direction (a from-node and a to-node), which allows adjacency information to be determined (Figure 6.3: “Polygon Topology”). Polygons that share an arc are deemed adjacent, or contiguous, and therefore the “left,” and “right” side of each arc can be defined. This left and right polygon information are stored explicitly within the attribute information of the topological data model. The “universe polygon” is an essential component of polygon topology that represents the external area located outside of the study area. Figure 6.3: “Polygon Topology” shows that arc 6 is bound on the left by polygon B and to the right by polygon C. Polygon A, the universe polygon, is to the left of arcs 1, 2, and 3.
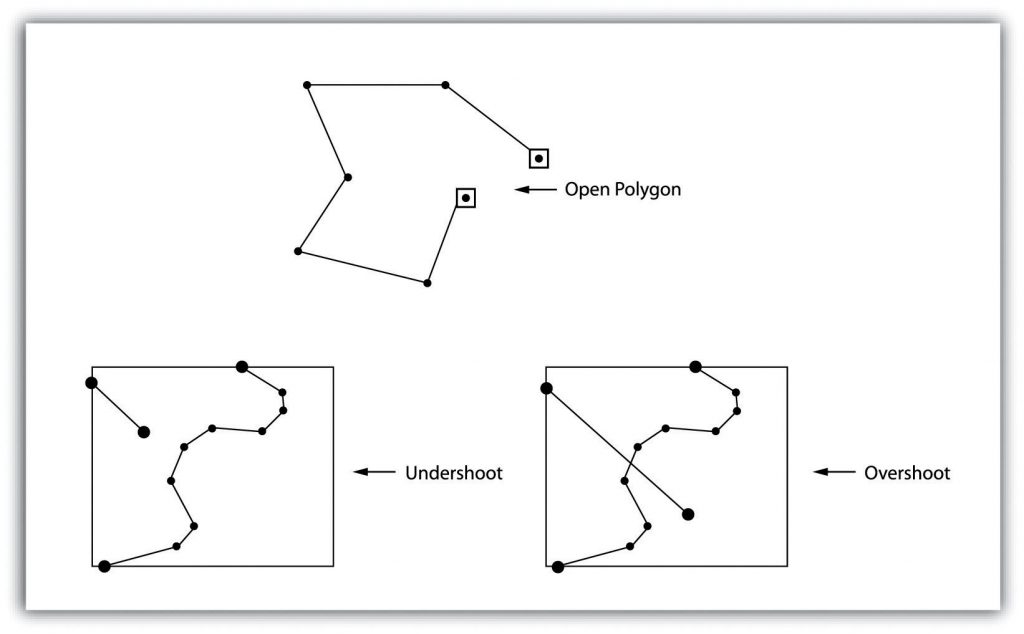
Topology allows the computer to rapidly determine and analyze the spatial relationships of all its included features. Also, topological information is essential because it allows for efficient error detection within a vector dataset. In the case of polygon features, open or unclosed polygons, which occur when an arc does not completely loop back upon itself, and unlabeled polygons, which occur when an area does not contain any attribute information, violate polygon-arc topology rules. Another topological error found with polygon features is the sliver. Slivers occur when the shared boundary of two polygons do not meet precisely. In the case of line features, topological errors occur when two lines do not meet perfectly at a node. This error is called an “undershoot” when the lines do not extend far enough to meet each other and an “overshoot” when the line extends beyond the feature it should connect to (Figure 6.4: “Common Topological Errors”). The result of overshoots and undershoots is a “dangling node” at the end of the line. Dangling nodes are not always an error, however, as they occur in the case of dead-end streets on a road map.
Many types of spatial analysis require the degree of organization offered by topologically explicit data models. In particular, network analysis (e.g., finding the best route from one location to another) and measurement (e.g., finding the length of a river segment) relies heavily on the concept of to- and from-nodes. It uses this information, along with attribute information, to calculate distances, shortest routes, quickest routes, and so forth. Topology also allows for sophisticated neighborhood analysis such as determining adjacency, clustering, nearest neighbors. Now that the basics of the concepts of topology have been outlined, we can begin to understand the topological data model better. In this model, the node acts as more than just a simple point along a line or polygon. The node represents the point of intersection for two or more arcs. Arcs may or may not be looped into polygons. Regardless, all nodes, arcs, and polygons are individually numbered. This numbering allows for quick and easy reference within the data model.
Single-Layer Analysis
As the name suggests, single layer analyses are those that are undertaken on an individual feature dataset. Buffering is the process of creating an output polygon layer containing a zone (or zones) of a specified width around an input point, line, or polygon feature. Buffers are particularly suited for determining the area of influence around features of interest. Geoprocessing is a suite of tools provided by many geographic information system (GIS) software packages that allow the user to automate many of the mundane tasks associated with manipulating GIS data. Geoprocessing usually involves the input of one or more feature datasets, followed by a spatially explicit analysis, and resulting in an output feature dataset.
Buffering
Buffers are common vector analysis tools used to address questions of proximity in a GIS and can be used on points, lines, or polygons (Figure 6.5: “Buffers around Red Point, Line, and Polygon Features”). For instance, suppose that a natural resource manager wants to ensure that no areas are disturbed within 1,000 feet of breeding habitat for the federally endangered Delhi Sands flower-loving fly. This species is found only in the few remaining Delhi Sands soil formations of the western United States. To accomplish this task, a 1,000-foot protection zone (buffer) could be created around all the observed point locations of the species. Alternatively, the manager may decide that there is not enough point-specific location information related to this rare species and decide to protect all Delhi Sands soil formations. In this case, he or she could create a 1,000-foot buffer around all polygons labeled as “Delhi Sands” on a soil formations dataset. In either case, the use of buffers provides a quick-and-easy tool for determining which areas are to be maintained as preserved habitat for the endangered fly.
Several buffering options are available to refine the output. For example, the buffer tool will typically buffer only selected features. If no features are selected, all features will be buffered. Two primary types of buffers are available to the GIS users: constant width and variable width. Constant width buffers require users to input a value by which features are buffered (Figure 6.5: “Buffers around Red Point, Line, and Polygon Features”), such as is seen in the examples in the preceding paragraph. Variable width buffers, on the other hand, call on a premade buffer field within the attribute table to determine the buffer width for each specific feature in the dataset (Figure 6.6: “Additional Buffer Options around Red Features: (a) Variable Width Buffers, (b) Multiple Ring Buffers, (c) Doughnut Buffer, (d) Setback Buffer, (e) Nondissolved Buffer, (f) Dissolved Buffer”).
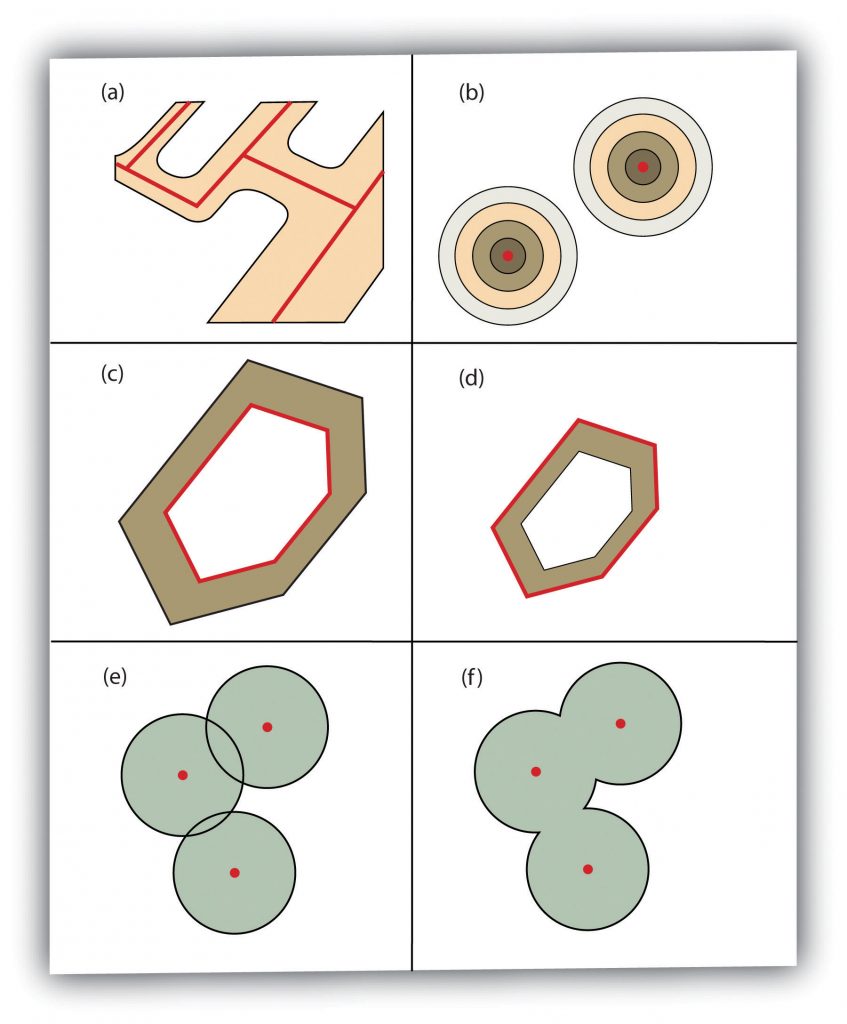
Besides, users can choose to dissolve or not dissolve the boundaries between overlapping, coincident buffer areas. Multiple ring buffers can be made such that a series of concentric buffer zones (much like an archery target) is created around the originating feature at user-specified distances (Figure 6.6: “Additional Buffer Options around Red Features: (a) Variable Width Buffers, (b) Multiple Ring Buffers, (c) Doughnut Buffer, (d) Setback Buffer, (e) Nondissolved Buffer, (f) Dissolved Buffer”). In the case of polygon layers, buffers can be created that includes the originating polygon feature as part of the buffer, or they are created as a doughnut buffer that excludes the input polygon area. Setback buffers are similar to doughnut buffers; however, they only buffer the area inside of the polygon boundary. Linear features can be buffered on both sides of the line, only on the left, or only on the right. Linear features can also be buffered so that the endpoints of the line are rounded (ending in a half-circle) or flat (ending in a rectangle).
Geoprocessing Operations
“Geoprocessing” is a loaded term in the field of GIS. The term can (and should) be widely applied to any attempt to manipulate GIS data. However, the term came into common usage due to its application to a somewhat arbitrary suite of single layer and multiple layer analytical techniques in the Geoprocessing Wizard of ESRI’s ArcView software package in the mid-1990s. Regardless, the suite of geoprocessing tools available in a GIS greatly expands and simplifies many of the management and manipulation processes associated with vector feature datasets. The primary use of these tools is to automate the repetitive preprocessing needs of typical spatial analyses and to assemble exact graphical representations for subsequent analysis and/or inclusion in presentations and final mapping products. The union, intersect, symmetrical difference, and identity overlay methods discussed in the section “Other Multilayer Geoprocessing Options” are often used in conjunction with these geoprocessing tools. The following represents the most common geoprocessing tools.
The dissolve operation combines adjacent polygon features in a single feature dataset based on a single predetermined attribute. For example, part (a) of Figure 6.7: “Single Layer Geoprocessing Functions” shows the boundaries of seven different parcels of land, owned by four different families (labeled 1 through 4). The dissolve tool automatically combines all adjacent features with the same attribute values. The result is an output layer to the same extent as the original but without all of the unnecessary, intervening line segments. The dissolved output layer is much easier to interpret when the map is classified according to the dissolved field visually.
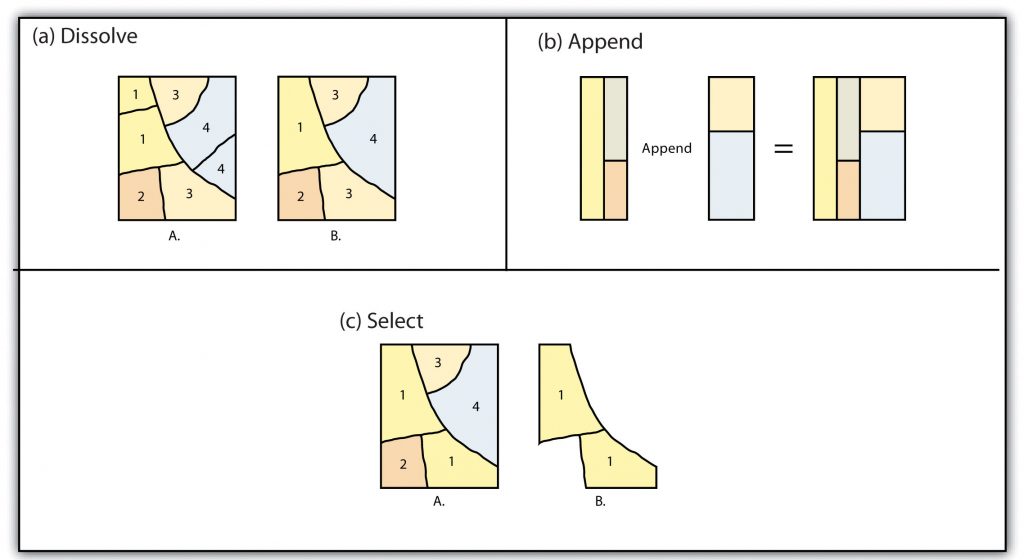
The append operation creates an output polygon layer by combining the spatial extent of two or more layers (part (d) of Figure 6.7: “Single Layer Geoprocessing Functions”). For use with a point, line, and polygon datasets, the output layer will be the same feature type as the input layers (which must each be the same feature type as well). Unlike the dissolve tool, append does not remove the boundary lines between appended layers (in the case of lines and polygons). Therefore, it is often useful to perform a dissolve after the use of the append tool to remove these potentially unnecessary dividing lines. Append is frequently used to mosaic data layers, such as digital US Geological Survey (USGS) 7.5-minute topographic maps, to create a single map for analysis and/or display.
The select operation creates an output layer based on a user-defined query that selects particular features from the input layer (part (f) of Figure 6.7: “Single Layer Geoprocessing Functions”). The output layer contains only those features that are selected during the query. For example, a city planner may choose to perform a select on all areas that are zoned “residential,” so he or she can quickly assess which areas in town are suitable for a proposed housing development.
Finally, the merge operation combines features within a point, line, or polygon layer into a single feature with identical attribute information. Often, the original features will have different values for a given attribute. In this case, the first attribute encountered is carried over into the attribute table, and the remaining attributes are lost. This operation is particularly useful when polygons are found to be unintentionally overlapping. Merge will conveniently combine these features into a single entity.
Multiple-Layer Analysis
Among the most powerful and commonly used tools in a geographic information system (GIS) is the overlay of cartographic information. In a GIS, an overlay is a process of taking two or more different thematic maps of the same area and placing them on top of one another to form a new map. Inherent in this process, the overlay function combines not only the spatial features of the dataset but also the attribute information as well.
A typical example used to illustrate the overlay process is, “Where is the best place to put a mall?” Imagine you are a corporate bigwig and are tasked with determining where your company’s next shopping mall will be placed. How would you attack this problem? With a GIS at your command, answering such spatial questions begins with amassing and overlaying pertinent spatial data layers. For example, you may first want to determine what areas can support the mall by accumulating information on which land parcels are for sale and which are zoned for commercial development. After collecting and overlaying the baseline information on available development zones, you can begin to determine which areas offer the most economic opportunity by collecting regional information on average household income, population density, location of proximal shopping centers, local buying habits, and more. Next, you may want to collect information on restrictions or roadblocks to development such as the cost of land, cost to develop the land, community response to development, adequacy of transportation corridors to and from the proposed mall, tax rates. Indeed, merely collecting and overlaying spatial datasets provides a valuable tool for visualizing and selecting the optimal site for such a business endeavor.
Overlay Operations
Several basic overlay processes are available in a GIS for vector datasets: point-in-polygon, polygon-on-point, line-on-line, line-in-polygon, polygon-on-line, and polygon-on-polygon. As you may be able to divine from the names, one of the overlay datasets must always be a line or polygon layer, while the second may be a point, line, or polygon. The new layer produced following the overlay operation is termed the “output” layer.
The point-in-polygon overlay operation requires a point input layer and a polygon overlay layer. Upon performing this operation, a new output point layer is returned that includes all the points that occur within the spatial extent of the overlay (Figure 6.8: “A Map Overlay Combining Information from Point, Line, and Polygon Vector Layers, as Well as Raster Layers”). Also, all the points in the output layer contain their original attribute information, as well as the attribute information from the overlay. For example, suppose you were tasked with determining if an endangered species residing in a national park was found primarily in a particular vegetation community. The first step would be to acquire the point occurrence locales for the species in question, plus a polygon overlay layer showing the vegetation communities within the national park boundary. Upon performing the point-in-polygon overlay operation, a new point file is created that contains all the points that occur within the national park. The attribute table of this output point file would also contain information about the vegetation communities being utilized by the species at the time of observation. A quick scan of this output layer and its attribute table would allow you to determine where the species was found in the park and to review the vegetation communities in which it occurred. This process would enable park employees to make informed management decisions regarding which onsite habitats to protect to ensure continued site utilization by the species.
As its name suggests, the polygon-on-point overlay operation is the opposite of the point-in-polygon operation. In this case, the polygon layer is the input, while the point layer is the overlay. The polygon features that overlay these points are selected and subsequently preserved in the output layer. For example, given a point dataset containing the location of some type of crime and a polygon dataset representing city blocks, a polygon-on-point overlay operation would allow police to select the city blocks in which crimes have been known to occur and hence determine those locations where an increased police presence may be warranted.
A line-on-line overlay operation requires line features for both the input and the overlay layer. The output from this operation is a point or points located precisely at the intersection(s) of the two linear datasets (Figure 6.9: “Line-on-Line Overlay”). For example, a linear feature dataset containing railroad tracks may be overlain on the linear road network. The resulting point dataset contains all the locales of the railroad crossings over a town’s road network. The attribute table for this railroad crossing point dataset would contain information on both the railroad and the road over which it passed.
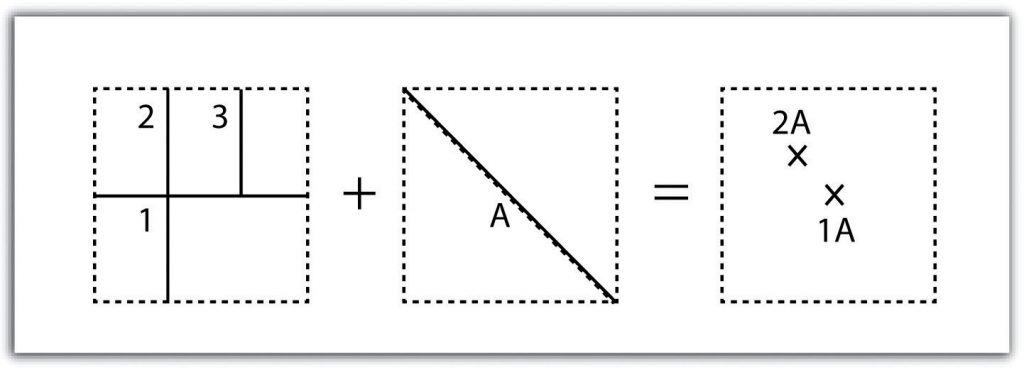
The line-in-polygon overlay operation is similar to the point-in-polygon overlay, with that obvious exception that a line input layer is used instead of a point input layer. In this case, each line that has any part of its extent within the overlay polygon layer will be included in the output line layer. However, these lines will be truncated at the boundary of the overlay (Figure 6.10: “Polygon-on-Line Overlay”). For example, a line-in-polygon overlay can take an input layer of interstate line segments and a polygon overlay representing city boundaries and produce a linear output layer of highway segments that fall within the city boundary. The attribute table for the output interstate line segment will contain information on the interstate name as well as the city through which they pass.
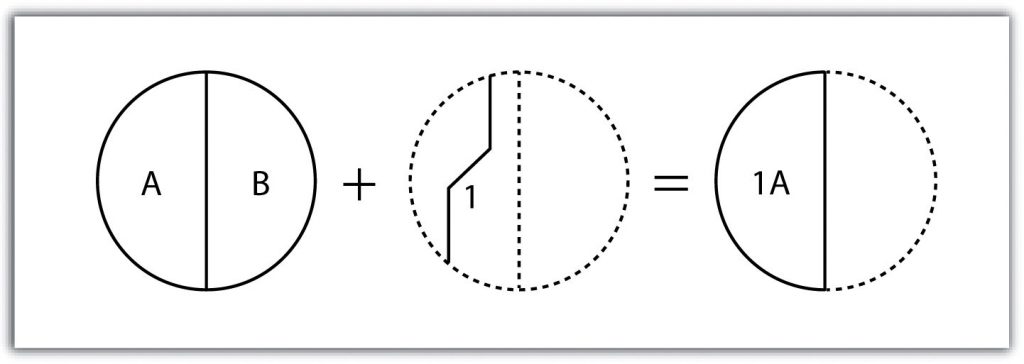
The polygon-on-line overlay operation is the opposite of the line-in-polygon operation. In this case, the polygon layer is the input, while the line layer is the overlay. The polygon features that overlay these lines are selected and subsequently preserved in the output layer. For example, given a layer containing the path of a series of telephone poles/wires and a polygon map contain city parcels, a polygon-on-line overlay operation would allow a land assessor to select those parcels containing overhead telephone wires.
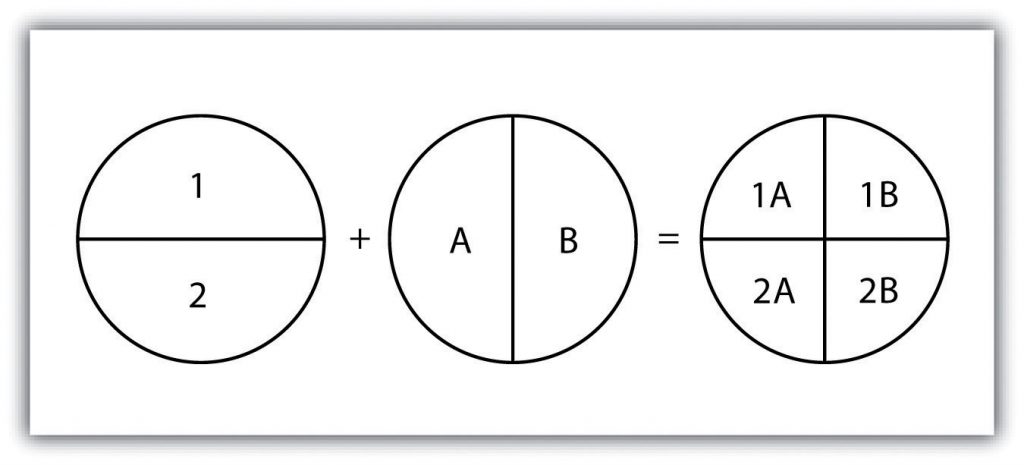
Finally, the polygon-in-polygon overlay operation employs a polygon input and a polygon overlay. This is the most commonly used overlay operation. Using this method, the polygon input and overlay layers are combined to create an output polygon layer with the extent of the overlay. The attribute table will contain spatial data and attribute information from both the input and overlay layers (Figure 6.11: “Polygon-in-Polygon Overlay”). For example, you may choose an input polygon layer of soil types with an overlay of agricultural fields within a given county. The output polygon layer would contain information on both the location of agricultural fields and soil types throughout the county.
The overlay operations discussed previously assume that the user desires the overlain layers to be combined. This is not always the case. Overlay methods can be more complicated than that and therefore employ the basic Boolean operators: AND, OR, and XOR. Depending on which operator(s) are utilized, the overlay method employed will result in an intersection, union, symmetrical difference, or identity.
Specifically, the union overlay method employs the OR operator. A union can be used only in the case of two polygon input layers. It preserves all features, attributes information, and spatial extents from both input layers (part (a) of Figure 6.12: “Vector Overlay Methods “). This overlay method is based on the polygon-in-polygon operation described in the section “Buffering.”
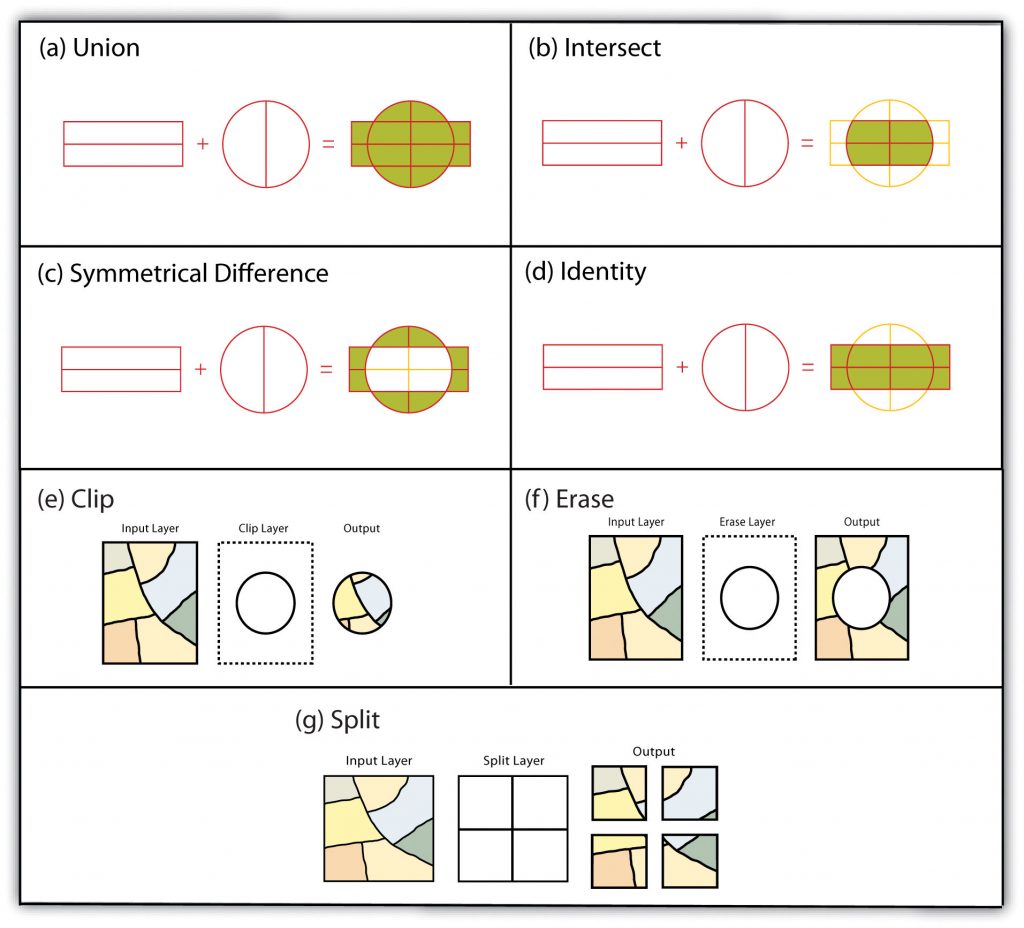
Alternatively, the intersection overlay method employs the AND operator. An intersection requires a polygon overlay, but can accept a point, line, or polygon input. The output layer covers the spatial extent of the overlay and contains features and attributes from both the input and overlay (part (b) of Figure 6.12: “Vector Overlay Methods “).
The symmetrical difference overlay method employs the XOR operator, which results in the opposite output as an intersection. This method requires both input layers to be polygons. The output polygon layer produced by the symmetrical difference method represents those areas common to only one of the feature datasets (part (c) of Figure 6.12: “Vector Overlay Methods “).
In addition to these simple operations, the identity (also referred to as “minus”) overlay method creates an output layer with the spatial extent of the input layer (part (d) of Figure 6.12: “Vector Overlay Methods “) but includes attribute information from the overlay (referred to as the “identity” layer, in this case). The input layer can be points, lines, or polygons. The identity layer must be a polygon dataset.
Other Multilayered Geoprocessing Options
In addition to the vector, as mentioned earlier, overlay methods, other common multiple-layer geoprocessing options are available to the user. These included the clip, erase, and split tools. The clip geoprocessing operation is used to extract those features from an input point, line, or polygon layer that falls within the spatial extent of the clip layer (part (e) of Figure 6.12: “Vector Overlay Methods “). Following the clip, all attributes from the preserved portion of the input layer are included in the output. If any features are selected during this process, only those selected features within the clip boundary will be included in the output. For example, the clip tool could be used to clip the extent of a river floodplain by the extent of a county boundary. This would provide county managers with insight into which portions of the floodplain they are responsible for maintaining. This is similar to the intersect overlay method; however, the attribute information associated with the clip layer is not carried into the output layer following the overlay.
The erase geoprocessing operation is essentially the opposite of a clip. Whereas the clip tool preserves areas within an input layer, the erase tool preserves only those areas outside the extent of the analogous erase layer (part (f) of Figure 6.12: “Vector Overlay Methods “). While the input layer can be a point, line, or polygon dataset, the erase layer must be a polygon dataset. Continuing with our clip example, county managers could then use the erase tool to erase the areas of private ownership within the county floodplain area. Officials could then focus specifically on public reaches of the countywide floodplain for their upkeep and maintenance responsibilities.
The split geoprocessing operation is used to divide an input layer into two or more layers based on a split layer (part (g) of Figure 6.12: “Vector Overlay Methods “). The split layer must be a polygon, while the input layers can be a point, line, or polygon. For example, a homeowner’s association may choose to split up a countywide soil series map by parcel boundaries, so each homeowner has a specific soil map for their parcel.
Spatial Join
A spatial join is a hybrid between an attribute operation and a vector overlay operation. A spatial join results in the combination of two feature dataset tables by a common attribute field. Unlike the attribute operation, a spatial join determines which fields from a source layer’s attribute table are appended to the destination layer’s attribute table based on the relative locations of selected features. This relationship is explicitly based on the property of proximity or containment between the source and destination layers. The proximity option is used when the source layer is a point or line feature dataset, while the containment option is used when the source layer is a polygon feature dataset.
When employing the proximity (or “nearest”) option, a record for each feature in the source layer’s attribute table is appended to the closest given feature in the destination layer’s attribute table. The proximity option will typically add a numerical field to the destination layer attribute table, called “Distance,” within which the measured distance between the source and destination feature is placed. For example, suppose a city agency had a point dataset showing all known polluters in town and a line dataset of all the river segments within the municipal boundary. This agency could then perform a proximity-based spatial join to determine the nearest river segment that would most likely be affected by each polluter.
When using the containment (or “inside”) option, a record for each feature in the polygon source layer’s attribute table is appended to the record in the destination layer’s attribute table that it contains. If a destination layer feature (point, line, or polygon) is not entirely contained within a source polygon, no value will be appended. For example, suppose a pool cleaning business wanted to hone its marketing services by providing flyers only to homes that owned a pool. They could obtain a point dataset containing the location of every pool in the county and a polygon parcel map for that same area. That business could then conduct a spatial join to append the parcel information to the pool locales. This would provide them with information on each land parcel that contained a pool, and they could subsequently send their mailers only to those homes.
Overlay Errors
Although overlays are one of the essential tools in a GIS analyst’s toolbox, some problems can arise when using this methodology. In particular, slivers are a common error produced when two slightly misaligned vector layers are overlain (Figure 6.13: “Slivers”). This misalignment can come from several sources, including digitization errors, interpretation errors, or source map errors. Introduction to Geographic Information Systems. New York: McGraw-Hill. For example, most vegetation and soil maps are created from field survey data, satellite images, and aerial photography. While you can imagine that the boundaries of soils and vegetation frequently coincide, the fact that different researchers most likely created them at different times suggests that their boundaries will not entirely overlap. To remedy this problem, GIS software incorporates a cluster tolerance option that forces nearby lines to be snapped together if they fall within a user-specified distance. Care must be taken when assigning cluster tolerance. Too strict a setting will not snap shared boundaries, while too lenient a setting will snap unintended, neighboring boundaries together.
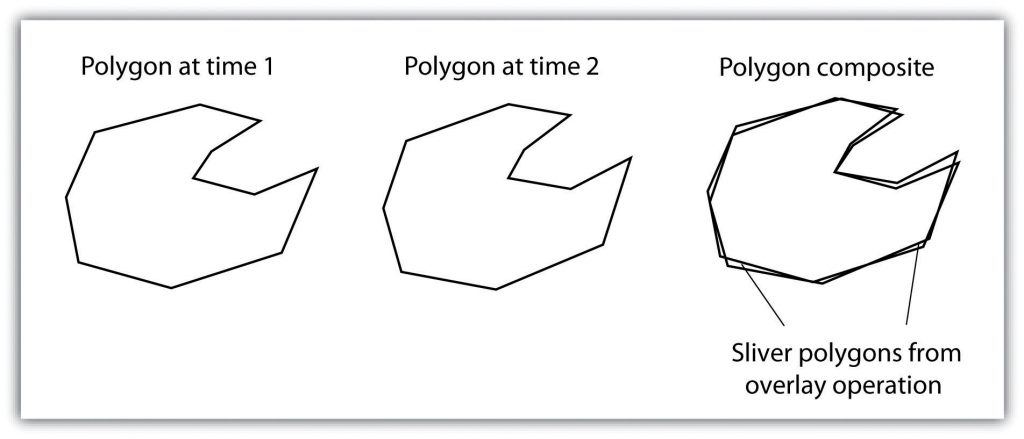
A second potential source of error associated with the overlay process is error propagation. Error propagation arises when inaccuracies are present in the original input and overlay layers and are propagated through to the output layer. These errors can be related to positional inaccuracies of the points, lines, or polygons. Alternatively, they can arise from attribute errors in the original data table(s). Regardless of the source, error propagation represents a common problem in overlay analysis, the impact of which depends mainly on the accuracy and precision requirements of the project at hand.
Advantages and Disadvantages of Vector Models
In comparison with the raster data model, vector data models tend to be better representations of reality due to the accuracy and precision of points, lines, and polygons over the regularly spaced grid cells of the raster model. This results in vector data tending to be more aesthetically pleasing than raster data.
Vector data also provides an increased ability to alter the scale of observation and analysis. As each coordinate pair associated with a point, line, and polygon represents an infinitesimally exact location (albeit limited by the number of significant digits and/or data acquisition methodologies), zooming deep into a vector image does not change the view of a vector graphic in the way that it does a raster graphic.
Vector data tend to be more compact in the data structure, so file sizes are typically much smaller than their raster counterparts. Although the ability of modern computers has minimized the importance of maintaining small file sizes, vector data often require a fraction of the computer storage space when compared to raster data.
The final advantage of vector data is that topology is inherent in the vector model. This topological information results in simplified spatial analysis (e.g., error detection, network analysis, proximity analysis, and spatial transformation) when using a vector model.
Alternatively, there are two primary disadvantages to the vector data model. First, the data structure tends to be much more complicated than the simple raster data model. As the location of each vertex must be stored explicitly in the model, there are no shortcuts for storing data like there are for raster models (e.g., the run-length and quad-tree encoding methodologies).
Second, the implementation of spatial analysis can also be relatively complicated due to minor differences in accuracy and precision between the input datasets. Similarly, the algorithms for manipulating and analyzing vector data are complex and can lead to intensive processing requirements, mainly when dealing with large datasets.
Zero-dimensional objects that contain only a single coordinate pair.
A common coordinate pair between intersecting lines or polygons.
Each bend along a line or polygon that is not the point of intersect.
Features composed of multiple, explicitly connected points.
Similar to the function of a line, but are curved.
Shapes created by multiple lines that loop back to create a “closed” feature.
A model in which each point is represented as a string of coordinate pairs with no inherent structure.
A model that is characterized by the inclusion of topological information within the dataset.
Rules that model the relationships between neighboring points or polygons, and determines how they share geometry.
The arc-node topology for the feature dataset.
An arc that connects to surround an area defining a polygon.
Polygons that share an arc are deemed adjacent. The side of each arc can be defined.
A common error produced when two slightly misaligned vector layers are overlain.
The process of creating an output polygon layer containing a zone (or zones) of a specified width around an input point, line, or polygon feature.
Specialized software tools used to compare, analyze, or manipulate map layers and their underlying geographic data to create new sets of data.
This process will require users to input a value by which features are buffered.
A premade buffer field within the attribute table to determine the buffer width for each specific feature in the dataset.
A buffer field that changes width.
A buffer that excludes the input polygon area.
Buffer that includes ONLY the input polygon area.
Combines adjacent polygon features in a single feature dataset based on a single predetermined attribute.
Combines the spatial extent of two or more layers to create a new output polygon.
An output layer based on the selection of a particular feature(s) from the input layer.
Combines features within a layer into a single feature with identical attribute information.
To lie on top of another.
This operation requires a point input layer and a polygon overlay layer. A new output point layer is returned that includes all the points that occur within the spatial extent of the overlay.
the polygon layer is the input, while the point layer is the overlay.
An operation that requires line features for both the input and overlay layer.
Similar to the point-in-polygon overlay, with that obvious exception that a line input layer is used instead of a point input layer.
The opposite of the line-in-polygon operation. In this case, the polygon layer is the input, while the line layer is the overlay.
This operation employs a polygon input and a polygon overlay.
Preserves all features, attribute information, and spatial extents from both input layers.
This method employs the AND operator.
Employs the XOR operator, which results in the opposite output as an intersection.
Also referred to as “minus”, this overlay method creates an output layer with the spatial extent of the input layer, but includes attribute information from the overlay.
A method that is used to extract features from an input point, line, or polygon layer that falls within the spatial extent of the clip layer.
Essentially the opposite of a clip. Whereas the clip tool preserves areas within an input layer, the erase tool preserves only those areas outside the extent of the analogous erase layer.
An operation that is used to divide an input layer into two or more layers based on a split layer.
A hybrid between an attribute operation and a vector overlay operation. It results in the combination of two feature dataset tables by a common attribute field.
A feature in GIS software that forces nearby lines to be snapped together if they fall within a user-specified distance.
Occurs when inaccuracies are present in the original input and overlay layers and are propagated through to the output layer.

