16 Chapter 16: Correlations
Hypothesis testing beyond t-tests and ANOVAs
There are several different types of correlation coefficients. A correlation coefficient is a measure that varies from -1 to 1, where a value of 1 represents a perfect positive relationship between the variables, 0 represents no relationship, and -1 represents a perfect negative relationship.
In this chapter we will focus on Pearson’s r, which is a measure of the strength of the linear relationship between two continuous variables. r was developed by Karl Pearson in the early 1900s. We will see r as a way to quantify the relation between two variables to describe a linear relationship.

Karl Pearson at his desk Source
Figure 1 shows examples of various levels of correlation using randomly generated data for two continuous variables (reporting Pearson’s rs). We will learn more about interpreting a correlation coefficient when we discuss direction and magnitude later in the chapter.
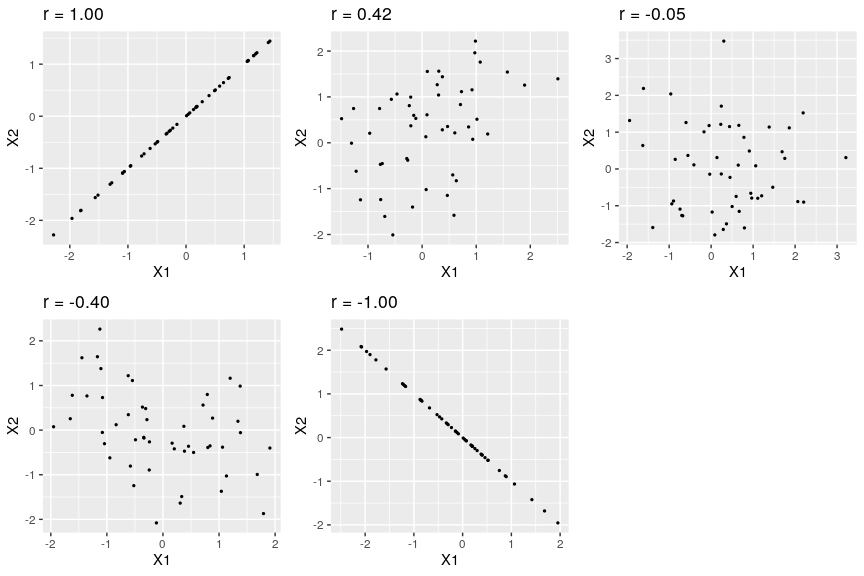
Figure 1: Examples of various levels of Pearson’s r.
Variability and Covariance
A common theme throughout statistics is the notion that individuals will differ on different characteristics and traits, which we call variance. In inferential statistics and hypothesis testing, our goal is to find systematic reasons for differences and rule out random chance as the cause. By doing this, we are using information on a different variable – which so far has been group membership like in ANOVA – to explain this variance. In correlations, we will instead use a continuous variable to account for the variance. Because we have two continuous variables, we will have two characteristics or score on which people will vary. What we want to know is do people vary on the scores together. That is, as one score changes, does the other score also change in a predictable or consistent way? This notion of variables differing together is called covariance (the prefix “co” meaning “together”).
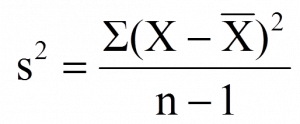
Covariance sample formula
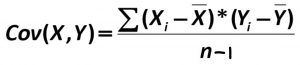
Sum of Products formula:
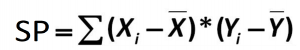
We will calculate the sum of products using the same table we used to calculate the sum of squares. In fact, the table for sum of products is simply a sum of squares table for X, plus a sum of squares table for Y, with a final column of products, as shown below.
|
X |
(X − ̅X) |
(X − ̅X)2 |
Y |
(Y − ̅Y) |
(Y − ̅Y)2 |
(X − ̅X)(Y − ̅Y) |
|
|
|
(if need s2) |
|
|
(if need s2) |
|
|
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
|
∑ (total up for SP) |
Table 1. Example for calculating Sum of Products
The previous paragraph brings us to an important definition about relations between variables. What we are looking for in a relation is a consistent or predictable pattern. That is, the variables change together, either in the same direction or opposite directions, in the same way each time. It doesn’t matter if this relation is positive or negative, only that it is not zero. If there is no consistency in how the variables change within a person, then the relation is zero and does not exist. We will revisit this notion of direction vs zero relation later on.
Visualizing Relations
Chapter 3 covered many different forms of data visualization, and visualizing data remains an important first step in understanding and describing out data before we move into inferential statistics. Nowhere is this more important than in correlation. Correlations are visualized by a scatterplot, where our X variable values are plotted on the X-axis, the Y variable values are plotted on the Y-axis, and each point or marker in the plot represents a single person’s score on X and Y. Figure 2 shows a scatterplot for hypothetical scores on job satisfaction (X) and worker well-being (Y). We can see from the axes that each of these variables is measured on a 10- point scale, with 10 being the highest on both variables (high satisfaction and good health and well-being) and 1 being the lowest (dissatisfaction and poor health).When we look at this plot, we can see that the variables do seem to be related. The higher scores on job satisfaction tend to also be the higher scores on well-being, and the same is true of the lower scores.
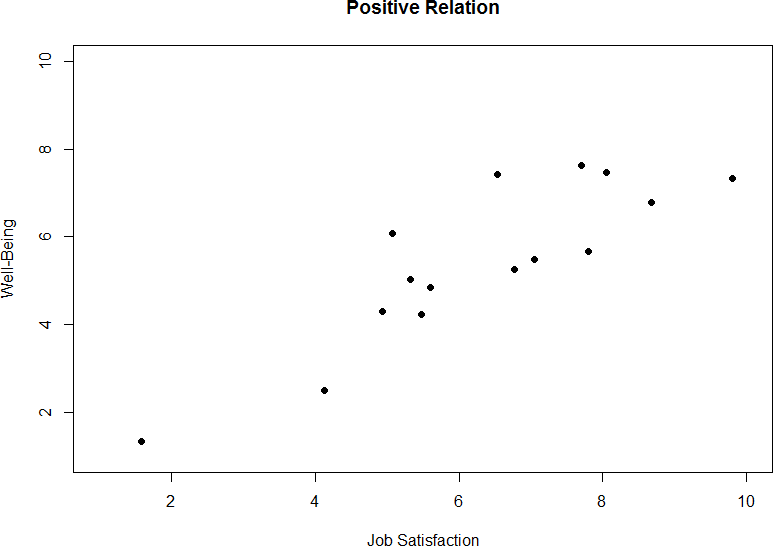
Figure 2. Plotting satisfaction and well-being scores.
Figure 2 demonstrates a positive relation. As scores on X increase, scores on Y also tend to increase. Although this is not a perfect relation (if it were, the points would form a single straight line), it is nonetheless very clearly positive. This is one of the key benefits to scatterplots: they make it very easy to see the direction of the relation. As another example, figure 3 shows a negative relation between job satisfaction (X) and burnout (Y). As we can see from this plot, higher scores on job satisfaction tend to correspond to lower scores on burnout, which is how stressed, unenergetic, and unhappy someone is at their job. As with figure 2, this is not a perfect relation, but it is still a clear one. As these figures show, points in a positive relation moves from the bottom left of the plot to the top right, and points in a negative relation move from the top left to the bottom right.
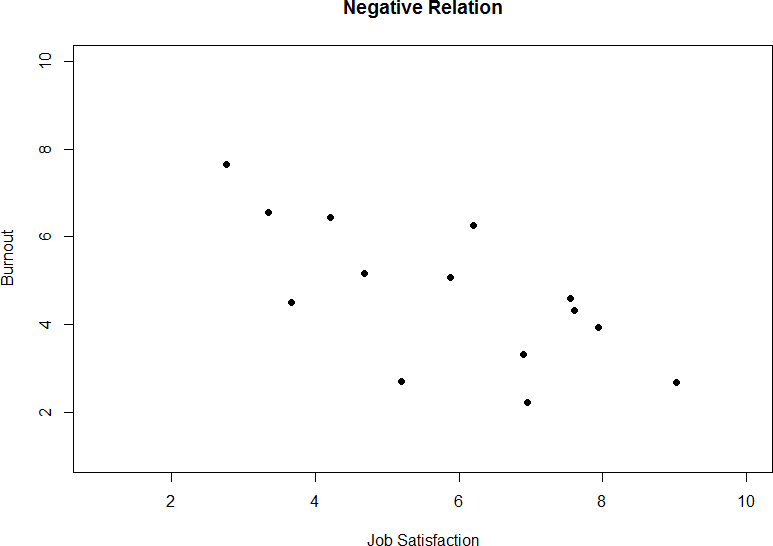
Figure 3. Plotting satisfaction and burnout scores.
As we can see, scatterplots are very useful for giving us an approximate idea of whether or not there is a relation between the two variables and, if there is, if that relation is positive or negative. They are also useful for another reason: they are the only way to determine one of the characteristics of correlations that are discussed next: form.
Figure 4. Plotting no relation between satisfaction and job performance.
Three Characteristics for Correlations
When we talk about correlations, there are three traits that we need to know in order to truly understand the relation (or lack of relation) between X and Y: form, direction, and magnitude. We will discuss each of them in turn.
Form
The first characteristic of relations between variables is their form. The form of a relation is the shape it takes in a scatterplot, and a scatterplot is the only way it is possible to assess the form of a relation. there are three forms we look for: linear, curvilinear, or no relation. A linear relation is what we saw in figures 1, 2, and 3. If we drew a line through the middle points in the any of the scatterplots, we would be best suited with a straight line. The term “linear” comes from the word “line”. A linear relation is what we will always assume when we calculate correlations. All of the correlations presented here are only valid for linear relations. Thus, it is important to plot our data to make sure we meet this assumption.
The relation between two variables can also be curvilinear. As the name suggests, a curvilinear relation is one in which a line through the middle of the points in a scatterplot will be curved rather than straight. Two examples are presented in figures 5 and 6.
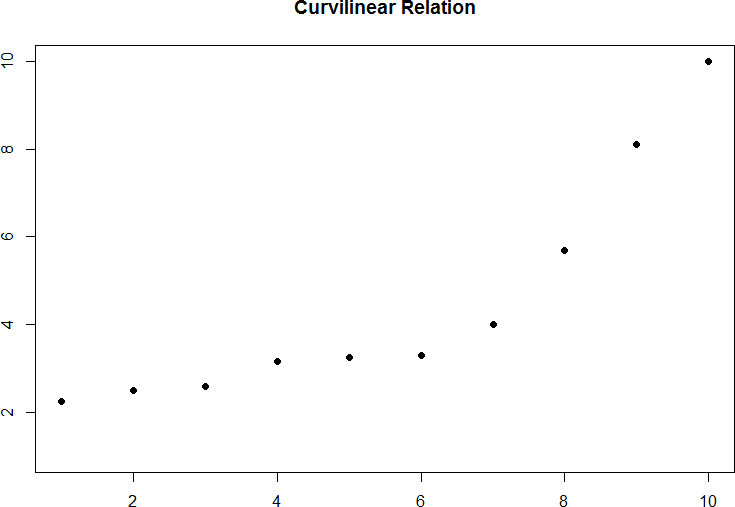
Figure 5. Exponentially increasing curvilinear relation
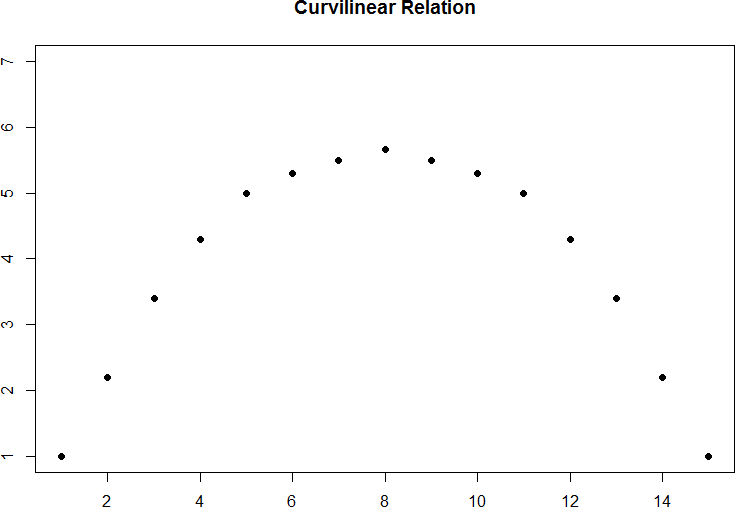
Figure 6. Inverted-U curvilinear relation.
Curvilinear relations can take many shapes, and the two examples above are only a small sample of the possibilities. What they have in common is that they both have a very clear pattern but that pattern is not a straight line. If we try to draw a straight line through them, we would get a result similar to what is shown in figure 7.
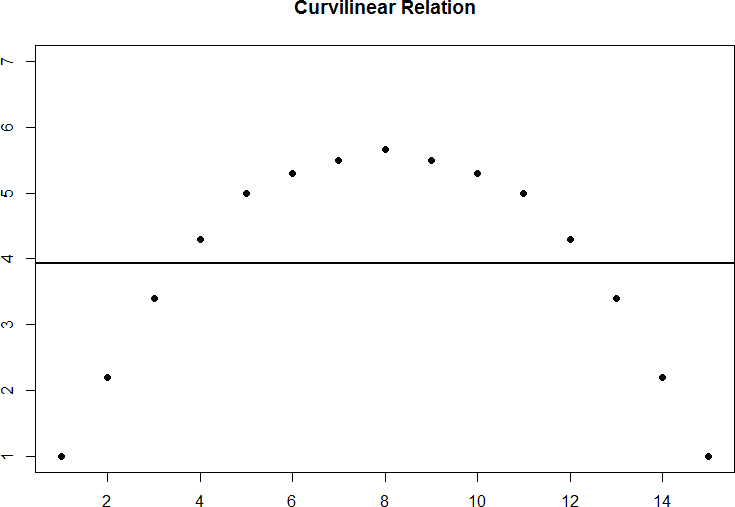
Figure 7. Overlaying a straight line on a curvilinear relation.
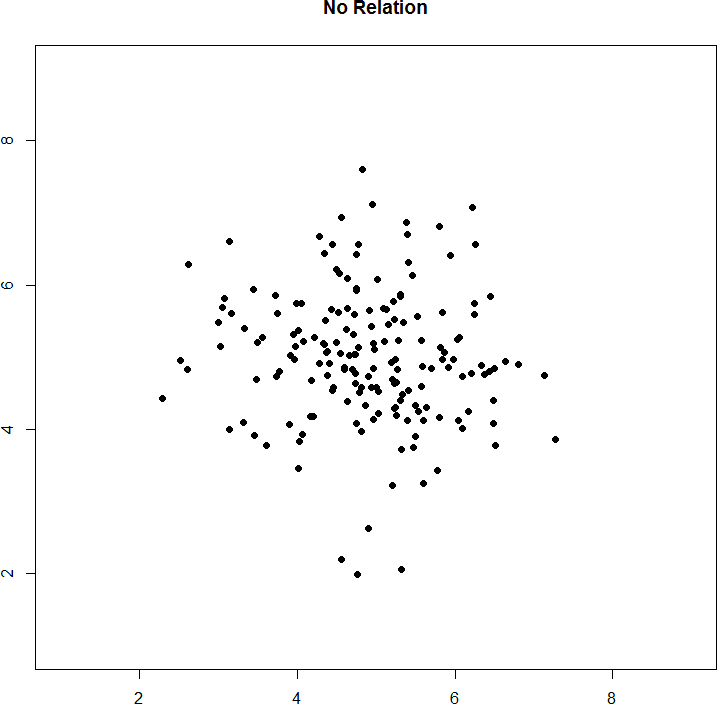
Figure 8. No relation
Direction
The direction of the relation between two variables tells us whether the variables change in the same way at the same time or in opposite ways at the same time. We saw this concept earlier when first discussing scatterplots, and we used the terms positive and negative. A positive relation is one in which X and Y change in the same direction: as X goes up, Y goes up, and as X goes down, Y also goes down. A negative relation is just the opposite: X and Y change together in opposite directions: as X goes up, Y goes down, and vice versa.
As we will see soon, when we calculate a correlation coefficient, we are quantifying the relation demonstrated in a scatterplot. That is, we are putting a number to it. That number will be either positive, negative, or zero, and we interpret the sign of the number as our direction. If the number is positive, it is a positive relation, and if it is negative, it is a negative relation. If it is zero, then there is no relation. The direction of the relation corresponds directly to the slope of the hypothetical line we draw through scatterplots when assessing the form of the relation. If the line has a positive slope that moves from bottom left to top right, it is positive, and vice versa for negative. If the line it flat, that means it has no slope, and there is no relation, which will in turn yield a zero for our correlation coefficient.
Magnitude
The number we calculate for our correlation coefficient, which we will describe in detail below, corresponds to the magnitude of the relation between the two variables. The magnitude is how strong or how consistent the relation between the variables is. Higher numbers mean greater magnitude, which means a stronger relation. Our correlation coefficients will take on any value between -1.00 and 1.00, with 0.00 in the middle, which again represents no relation. A correlation of -1.00 is a perfect negative relation; as X goes up by some amount, Y goes down by the same amount, consistently. Likewise, a correlation of 1.00 indicates a perfect positive relation; as X goes up by some amount, Y also goes up by the same amount. Finally, a correlation of 0.00, which indicates no relation, means that as X goes up by some amount, Y may or may not change by any amount, and it does so inconsistently.
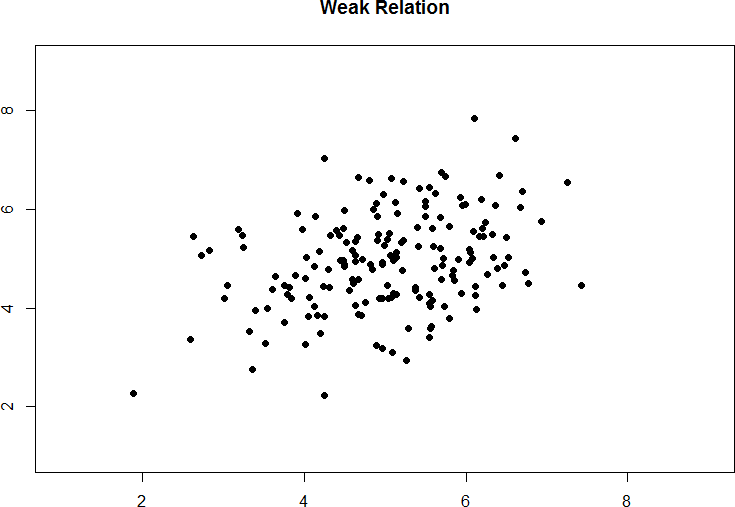
Figure 9. Weak positive correlation.
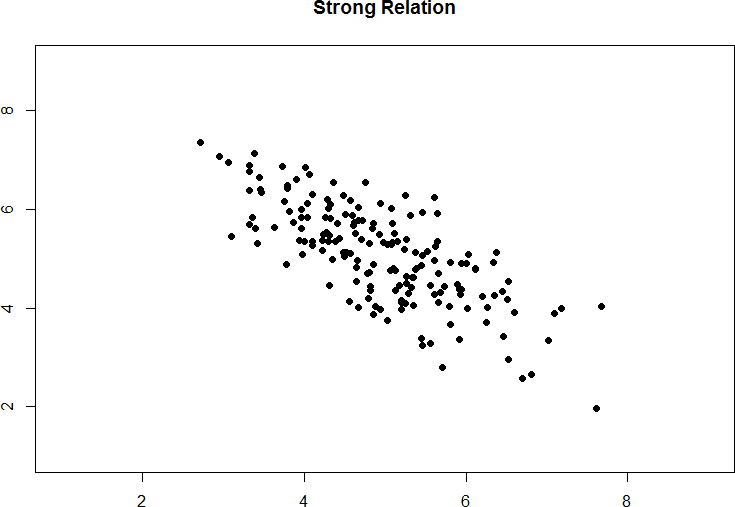
Figure 10. Strong negative correlation.
Pearson’s r
There are several different types of correlation coefficients, but we will only focus on the most common: Pearson’s r. r is a very popular correlation coefficient for assessing linear relations, and it serves as both a descriptive statistic (like ̅X aka M) and as a test statistic (like t). It is descriptive because it describes what is happening in the scatterplot; r will have both a sign (+/–) for the direction and a number (0 – 1 in absolute value) for the magnitude. As noted above, assumes a linear relation, so nothing about r will suggest what the form is – it will only tell what the direction and magnitude would be if the form is linear (Remember: always make a scatterplot first!). r also works as a test statistic because the magnitude of r will correspond directly to a t value as the specific degrees of freedom, which can then be compared to a critical value. Luckily, we do not need to do this conversion by hand. Instead, we will have a table of r critical values that looks very similar to our t table, and we can compare our r directly to those.
The conceptual formula for r is very simple: it is just the covariance (defined above) divided by the standard deviations of X and Y:
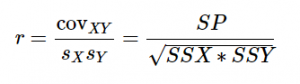
Note: This formula gives a direct sense of what a correlation is: a covariance standardized onto the scale of X and Y.
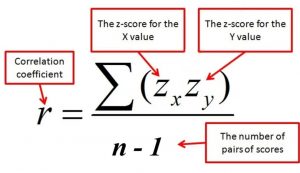
We can also compute Pearson another way. The second formula is computationally simpler and faster. Both of these equations will give the same value. When we do this calculation, we will find that our answer is always between -1.00 and 1.00 (if it’s not, check the math again), which gives us a standard, interpretable metric, similar to what z-scores did.
 If data population:
If data population: 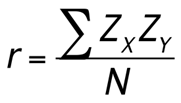
Correlation as a descriptive and as a test statistic
Correlation & z-scores

Table. 2.
The table 2 shows that positive products of Z scores contribute toward making a positive correlation, negative products of Z scores con- tribute toward making a negative correlation, and products of Z scores that are zero (or close to zero) contribute toward making a correlation of zero.
We still need to determine the strength of a positive or negative correlation on some standard scale. You cannot judge the strength of the correlation from the sum of the cross-products alone, because it gets bigger just by adding the cross-products of more people together.
The solution is to divide this sum of the cross-products by the number of people in the study. That is, you figure the average of the cross-products of Z scores.
It turns out that because of the nature of Z scores, this average can never be more than +1, which would be a positive linear perfect correlation. It can never be less than -1, which would be a negative linear perfect correlation.
In the situation of no linear correlation, the average of the cross-products of Z scores is 0.
Example: Anxiety and Depression
Anxiety and depression are often reported to be highly linked (or “comorbid”). Our hypothesis testing procedure follows the same four-step process as before, starting with our null and alternative hypotheses. We will look for a positive relation between our variables among a group of 10 people because that is what we would expect based on them being comorbid.
Step 1: State the Hypotheses
Our hypotheses for correlations start with a baseline assumption of no relation, and our alternative will be directional if we expect to find a specific type of relation. For this example, we expect a positive relation:
- H0: There is no relation between anxiety and depression, H0: ρ = 0
- HA: There is a positive relation between anxiety and depression, H0: ρ > 0
Step 2: Find the Critical Values
The critical values for correlations come from the correlation table, which looks very similar to the t-table (see figure 11). Just like our t-table, the column of critical values is based on our significance level (α) and the directionality of our test. The row is determined by our degrees of freedom. For correlations, we have n– 2 degrees of freedom, rather than n – 1 (why this is the case is not important at the moment). For our example, we have 10 people, so our degrees of freedom = 10 – 2 = 8.
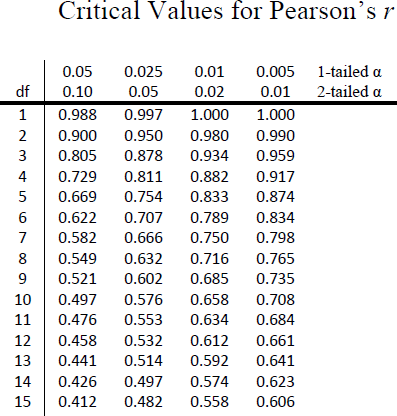
Figure 11. Correlation table
We were not given any information about the level of significance at which we should test our hypothesis, so we will assume α = 0.05 as always. From our table, we can see that a 1-tailed test (because we expect only a positive relation) at the α = 0.05 level has a critical value of r* = 0.549. Thus, if our observed correlation is greater than 0.549, it will be statistically significant. This is a rather high bar (remember, the guideline for a strong relation is r = 0.50); this is because we have so few people. Larger samples make it easier to find significant relations.
There are a few websites that share p-value calculators for correlations on the web. Here are a few options instead of using a table.
Step 3: Calculate the Test Statistic
We have laid out our hypotheses and the criteria we will use to assess them, so now we can move on to our test statistic. Before we do that, we must first create a scatterplot of the data to make sure that the most likely form of our relation is in fact linear. Figure 12 below shows our data plotted out, and it looks like they are, in fact, linearly related, so Pearson’s r is appropriate.
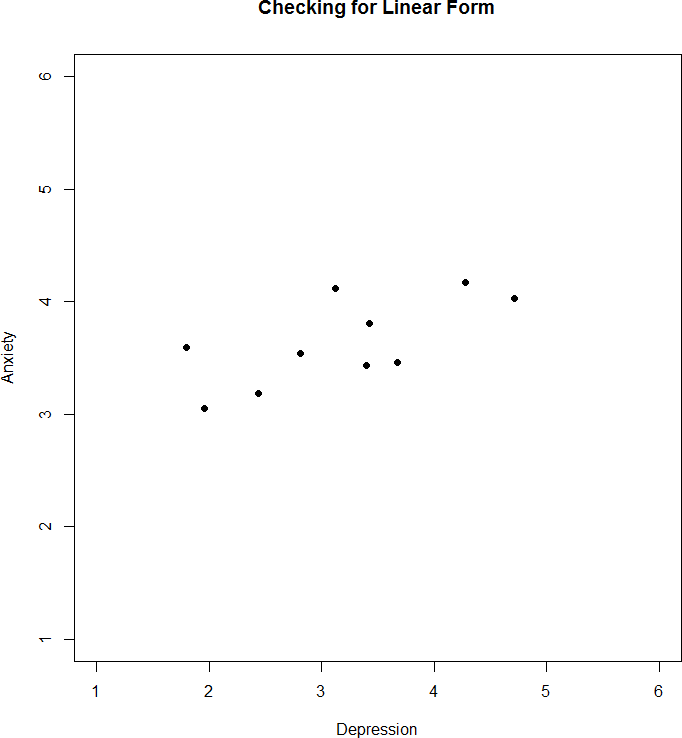
Figure 12. Scatterplot of anxiety and depression
The data we gather from our participants (n=10) is as follows:
|
Dep |
2.81 |
1.96 |
3.43 |
3.40 |
4.71 |
1.80 |
4.27 |
3.68 |
2.44 |
3.13 |
M = 3.16 |
s =0.89 |
SS = 7.97 |
|
Anx |
3.54 |
3.05 |
3.81 |
3.43 |
4.03 |
3.59 |
4.17 |
3.46 |
3.19 |
4.12 |
M = 3.64 |
s = 0.37 |
SS =1.33 |
Table 3. Data for step 3 to calculate r.
Steps for Calculating r using the computational formula:
- Change all scores to Z scores.
- This requires using the mean and the standard deviation of each variable, then changing each raw score to a Z score. This step is converting the raw scores to z-scores using the computational formula. See Table 4.
|
Dep |
2.81 |
1.96 |
3.43 |
3.40 |
4.71 |
1.80 |
4.27 |
3.68 |
2.44 |
3.13 |
M = 3.163 |
s =0.94 |
|
Anx |
3.54 |
3.05 |
3.81 |
3.43 |
4.03 |
3.59 |
4.17 |
3.46 |
3.19 |
4.12 |
M = 3.639 |
s = 0.38 |
Table 4. z-scores for anxiety and depression
- Figure the cross-product of the Z scores for each person. That is, for each person, multiply the person’s Z score on one variable by the person’s Z score on the other variable.
| Zx | Zy | Zx*Zy |
| -.38 | -0.26 | 0.10 |
| -1.28 | -1.55 | 1.98 |
| 0.28 | 0.45 | 0.13 |
| 0.25 | -0.55 | -0.14 |
| 1.65 | 1.03 | 1.69 |
| -1.45 | -0.13 | 0.19 |
| 1.78 | 1.0 | 1.65 |
| 0.55 | -0.47 | -0.26 |
| -0.77 | -1.18 | 0.91 |
| -0.04 | 1.27 | -0.04 |
| ∑ = 6.20 |
- Add up the cross-products of the Z scores for Sum of Products.
- Adding up the third column we get ∑ = 6.20.
- Divide by the n-1 using sample in the study.
- There were 10 participants in the study.
- 10-1 = 9
- 6.2/9 = .69
- Describe the relationship in words.
So our observed correlation between anxiety and depression is r = 0.69, which, based on sign and magnitude, is a strong, positive correlation. Now we need to compare it to our critical value to see if it is also statistically significant.
Besides statistics software, there are some Pearson (or Spearman) calculators on the web. Here are a few options if you are not required to do calculations or would like to check your work:
Step 4: Make a Decision
Our critical value was r* = 0.549 and our obtained value was r = 0.69. Our obtained value was larger than our critical value, so we can reject the null hypothesis.
Notice in our interpretation that, because we already know the magnitude and direction of our correlation, we can interpret that. We also report the degrees of freedom, just like with t, and we know that p < α because we rejected the null hypothesis. As we can see, even though we are dealing with a very different type of data, our process of hypothesis testing has remained unchanged.
Effect Size (step 5)
Pearson’s r is an incredibly flexible and useful statistic. Not only is it both descriptive and inferential, as we saw above, but because it is on a standardized metric (always between -1.00 and 1.00), it can also serve as its own effect size. In general, we use r = 0.10, r = 0.30, and r = 0.50 as our guidelines for small, medium, and large effects. Just like with Cohen’s d, these guidelines are not absolutes, but they do serve as useful indicators in most situations. Notice as well that these are the same guidelines we used earlier to interpret the magnitude of the relation based on the correlation coefficient.
The similarities between η2 and r2 in interpretation and magnitude should clue you in to the fact that they are similar analyses, even if they look nothing alike. That is because, behind the scenes, they actually are! In the next chapter, we will learn a technique called Linear Regression, which will formally link the two analyses together.
Correlation versus Causation
We cover a great deal of material in introductory statistics and, as mentioned chapter 1, many of the principles underlying what we do in statistics can be used in your day to day life to help you interpret information objectively and make better decisions. We now come to what may be the most important lesson in introductory statistics: the difference between correlation and causation.
A Reminder about Experimental Design
When we say that one thing causes another, what do we mean? There is a long history in philosophy of discussion about the meaning of causality, but in statistics one way that we commonly think of causation is in terms of experimental control. That is, if we think that factor X causes factor Y, then manipulating the value of X should also change the value of Y.
Often we would like to test causal hypotheses but we can’t actually do an experiment, either because it’s impossible (“What is the relationship between human carbon emissions and the earth’s climate?”) or unethical (“What are the effects of severe abuse on child brain development?”). However, we can still collect data that might be relevant to those questions. For example, we can potentially collect data from children who have been abused as well as those who have not, and we can then ask whether their brain development differs.
Let’s say that we did such an analysis, and we found that abused children had poorer brain development than non-abused children. Would this demonstrate that abuse causes poorer brain development? No. Whenever we observe a statistical association between two variables, it is certainly possible that one of those two variables causes the other. However, it is also possible that both of the variables are being influenced by a third variable; in this example, it could be that child abuse is associated with family stress, which could also cause poorer brain development through less intellectual engagement, food stress, or many other possible avenues. The point is that a correlation between two variables generally tells us that something is probably causing something else, but it doesn’t tell us what is causing what.
Final Considerations
Correlations, although simple to calculate, and be very complex, and there are many additional issues we should consider. We will look at two of the most common issues that affect our correlations, as well as discuss some other correlations and reporting methods you may encounter.
Range Restriction
The strength of a correlation depends on how much variability is in each of the variables X and Y. This is evident in the formula for Pearson’s r, which uses both covariance (based on the sum of products, which comes from deviation scores) and the standard deviation of both variables (which are based on the sums of squares, which also come from deviation scores). Thus, if we reduce the amount of variability in one or both variables, our correlation will go down. Failure to capture the full variability of a variability is called range restriction.
Take a look at figures 13 and 14 below. The first shows a strong relation (r = 0.67) between two variables. An oval is overlain on top of it to make the relation even more distinct. The second shows the same data, but the bottom half of the X variable (all scores below 5) have been removed, which causes our relation (again represented by a red oval) to become much weaker (r = 0.38). Thus range restriction has truncated (made smaller) our observed correlation.
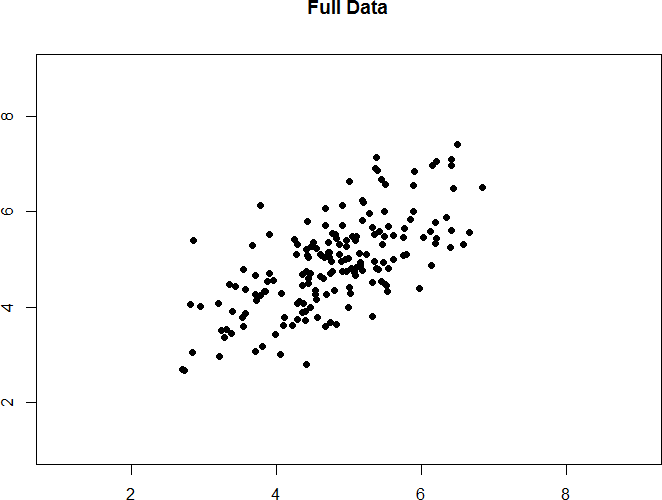
Figure 13. Strong, positive correlation.
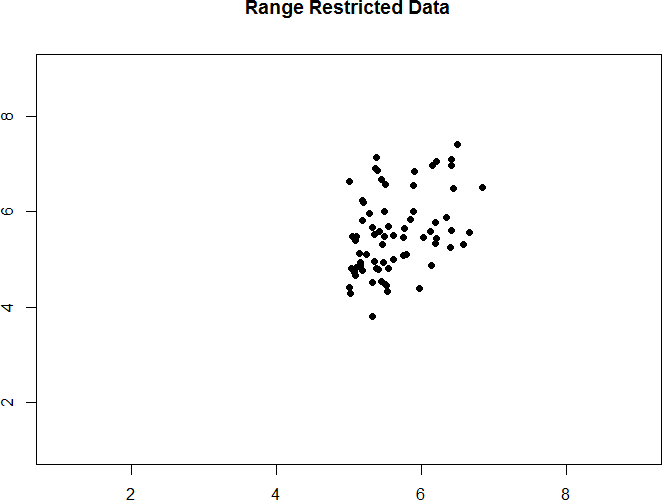
Figure 14. Effect of range restriction.
Sometimes range restriction happens by design. For example, we rarely hire people who do poorly on job applications, so we would not have the lower range of those predictor variables. Other times, we inadvertently cause range restriction by not properly sampling our population. Although there are ways to correct for range restriction, they are complicated and require much information that may not be known, so it is best to be very careful during the data collection process to avoid it.
Outliers
Another issue that can cause the observed size of our correlation to be inappropriately large or small is the presence of outliers. An outlier is a data point that falls far away from the rest of the observations in the dataset. Sometimes outliers are the result of incorrect data entry, poor or intentionally misleading responses, or simple random chance. Other times, however, they represent real people with meaningful values on our variables. The distinction between meaningful and accidental outliers is a difficult one that is based on the expert judgment of the researcher. Sometimes, we will remove the outlier (if we think it is an accident) or we may decide to keep it (if we find the scores to still be meaningful even though they are different).
Pearson’s r is sensitive to outliers. For example, in Figure 15 we can see how a single outlying data point can cause a very high positive correlation value, even when the actual relationship between the other data points is perfectly negative.
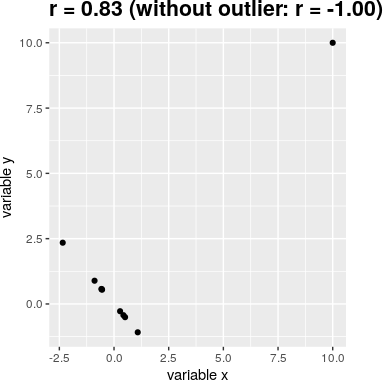
Figure 15. An simulated example of the effects of outliers on correlation. Without the outlier the remainder of the data points have a perfect negative correlation, but the single outlier changes the correlation value to highly positive.
One way to address outliers is to compute the correlation on the ranks of the data after ordering them, rather than on the data themselves; this is known as the Spearman correlation. Whereas the Pearson correlation for the example in Figure 15 was 0.83, the Spearman correlation is -0.45, showing that the rank correlation reduces the effect of the outlier and reflects the negative relationship between the majority of the data points.
Here are some more examples. The plots below in figure 16 show the effects that an outlier can have on data. In the first, we have our raw dataset. You can see in the upper right corner that there is an outlier observation that is very far from the rest of our observations on both the X and Y variables. In the middle, we see the correlation computed when we include the outlier, along with a straight line representing the relation; here, it is a positive relation. In the third image, we see the correlation after removing the outlier, along with a line showing the direction once again. Not only did the correlation get stronger, it completely changed direction!
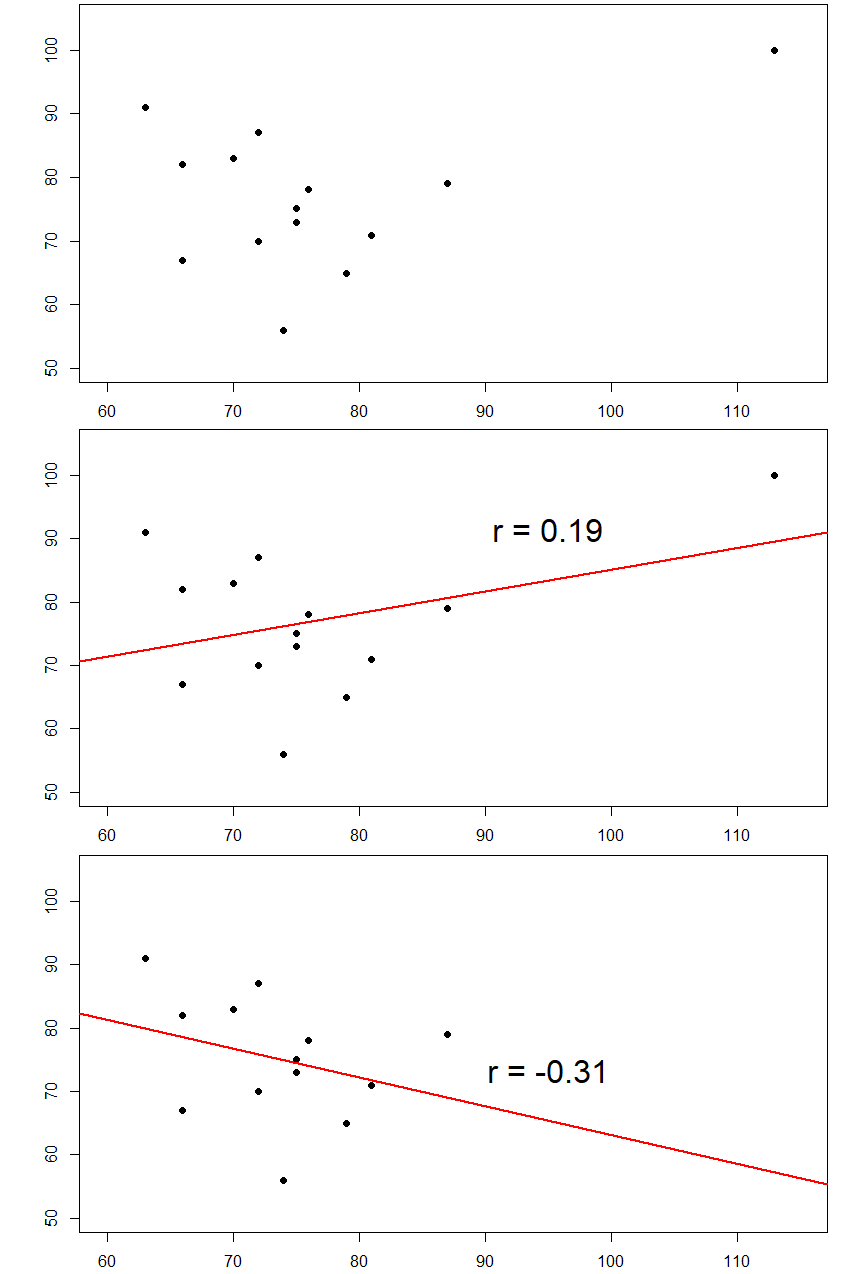
Figure 16. Three plots showing correlations with and without outliers.
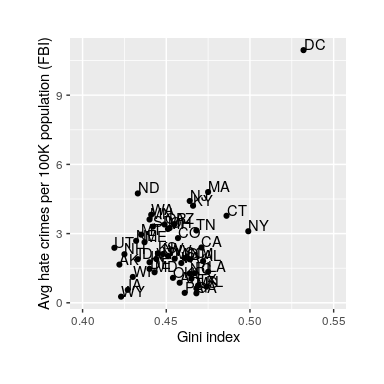
An misreported media example: Hate crimes and income inequality
In 2017, the web site Fivethirtyeight.com published a story titled Higher Rates Of Hate Crimes Are Tied To Income Inequality which discussed the relationship between the prevalence of hate crimes and income inequality in the wake of the 2016 Presidential election. The story reported an analysis of hate crime data from the FBI and the Southern Poverty Law Center, on the basis of which they report:
“we found that income inequality was the most significant determinant of population-adjusted hate crimes and hate incidents across the United States”.
The analysis reported in the story focused on the relationship between income inequality (defined by a quantity called the Gini index — see Appendix for more details) and the prevalence of hate crimes in each state.
Other Correlation Coefficients
In this chapter we have focused on Pearson’s r as our correlation coefficient because it very common and very useful. There are, however, many other correlations out there, each of which is designed for a different type of data. The most common of these is Spearman’s rho (ρ), which is designed to be used on ordinal data rather than continuous data. This is a very useful analysis if we have ranked data or our data do not conform to the normal distribution. There are even more correlations for ordered categories, but they are much less common and beyond the scope of this chapter.
Additionally, the principles of correlations underlie many other advanced analyses. In the next chapter, we will learn about regression, which is a formal way of running and analyzing a correlation that can be extended to more than two variables. Regression is a very powerful technique that serves as the basis for even our most advanced statistical models, so what we have learned in this chapter will open the door to an entire world of possibilities in data analysis.
Correlation Matrices
Many research studies look at the relation between more than two continuous variables. In such situations, we could simply list our all of our correlations, but that would take up a lot of space and make it difficult to quickly find the relation we are looking for. Instead, we create correlation matrices so that we can quickly and simply display our results. A matrix is like a grid that contains our values. There is one row and one column for each of our variables, and the intersections of the rows and columns for different variables contain the correlation for those two variables. At the beginning of the chapter, we saw scatterplots presenting data for correlations between job satisfaction, well-being, burnout, and job performance. We can create a correlation matrix to quickly display the numerical values of each. Such a matrix is shown below.
| Satisfaction | Well-Being | Burnout | Performance | |
| Satisfaction | 1.00 | |||
| Well-Being | 0.41 | 1.00 | ||
| Burnout | -0.54 | -0.87 | 1.00 | |
| Performance | 0.08 | 0.21 | -0.33 | 1.00 |
Table 6. Example Correlation Matrix
Notice that there are values of 1.00 where each row and column of the same variable intersect. This is because a variable correlates perfectly with itself, so the value is always exactly 1.00. Also notice that the upper cells are left blank and only the cells below the diagonal of 1s are filled in. This is because correlation matrices are symmetrical: they have the same values above the diagonal as below it. Filling in both sides would provide redundant information and make it a bit harder to read the matrix, so we leave the upper triangle blank. Correlation matrices are a very condensed way of presenting many results quickly, so they appear in almost all research studies that use continuous variables. Many matrices also include columns that show the variable means and standard deviations, as well as asterisks showing whether or not each correlation is statistically significant.
Summary
Value of the correlation coefficient (r)
- The value of r is always between –1 and +1
- The size of the correlation r indicates the strength of the linear relationship between x and y and values close to –1 or to +1 indicate a stronger linear relationship between x and y.
- o r = 1 represents a perfect positive correlation. A correlation of 1 indicates a perfect linear relationship.
- r = –1 represents a perfect negative correlation. A correlation of -1 indicates a perfect negative relationship.
- If r = 0 there is absolutely no linear relationship between x and y. A correlation of zero indicates no linear relationship.
Direction of the correlation coefficient (r)
- A positive value of r means that when x increases, y tends to increase and when x decreases, y tends to decrease (positive correlation).
- A negative value of r means that when x increases, y tends to decrease and when x decreases, y tends to increase (negative correlation).
If two variables have a significant linear correlation we normally might assume that there is something causing them to go together. However, we cannot know the direction of causality (what is causing what) just from the fact that the two variables are correlated.
Consider this example, the relationship between doing exciting activities with your significant other and satisfaction with the relationship. There are three possible directions of causality for these two variables:
- X could be causing Y
- Y could be causing X
- Some third factor could be causing both X and Y
These three possible directions of causality are shown in the figure below (b).
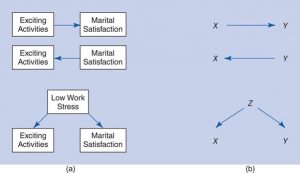
Figure 18. Three possible directions of causality (b) with examples (a)
- Correlation is a relationship that has established that X and Y are related – if we know one then the other can be predicted but we cannot conclude that one variable causes the other.
- Causation is a relationship for which we have to establish that X causes Y. To establish causation an experiment must demonstrate that Y can be controlled by presenting or removing X.
- For example, when we apply heat (X) the temperature of water (Y)increases and when we remove heat (X) the temperature of water (Y) decreases.
Learning Objectives
Having read this chapter, a student should be able to:
- Describe the concept of the correlation coefficient and its interpretation
- Understand Pearson correlation as a descriptive statistic and test statistic
- Compute the Pearson correlation
- Identify type of correlation based on the data (Pearson vs Spearman)
- Describe the effect of outlier data points and how to address them.
- Describe the potential causal influences that can give rise to an observed correlation.
Exercises – Ch. 16
- What does a correlation assess?
- What are the three characteristics of a correlation coefficient? Why is it important to visualize correlational data in a scatterplot before performing analyses?
- What sort of relation is displayed in the scatterplot below?
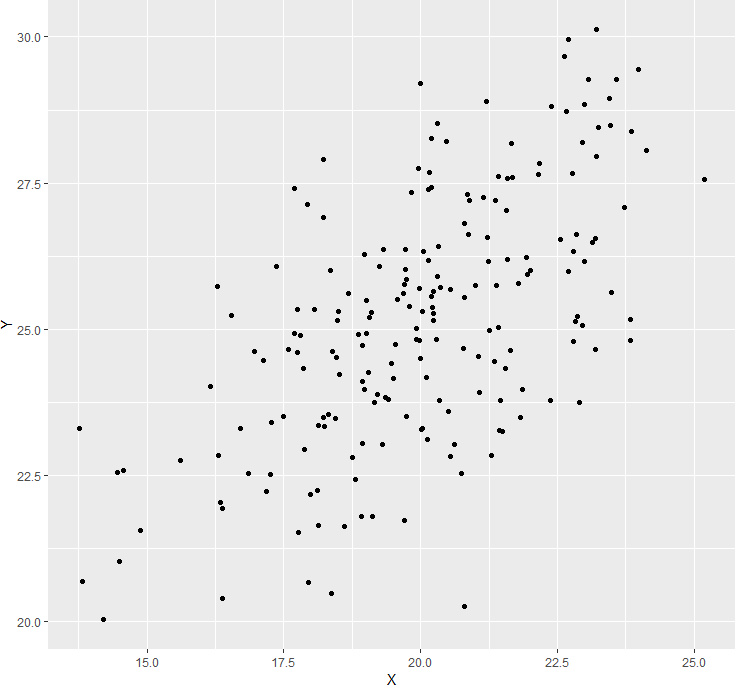
4. What is the direction and magnitude of the following correlation coefficients?
- -0.81
- 0.40
- 0.15
- -0.08
- 0.29
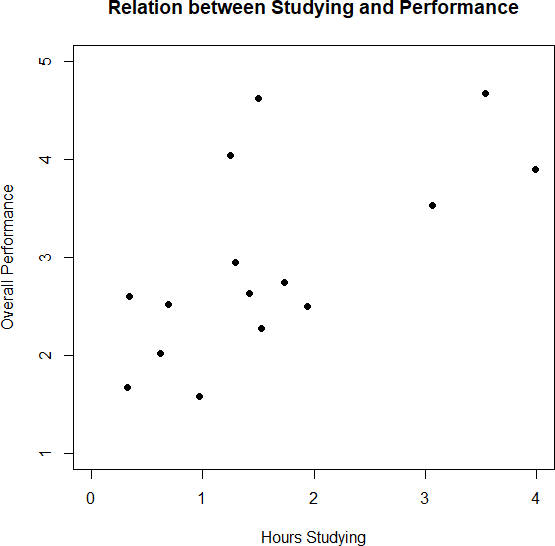
5. Create a scatterplot from the following data:
|
Hours Studying |
Overall Class Performance |
|
0.62 |
2.02 |
|
1.50 |
4.62 |
|
0.34 |
2.60 |
|
0.97 |
1.59 |
|
3.54 |
4.67 |
|
0.69 |
2.52 |
|
1.53 |
2.28 |
|
0.32 |
1.68 |
|
1.94 |
2.50 |
|
1.25 |
4.04 |
|
1.42 |
2.63 |
|
3.07 |
3.53 |
|
3.99 |
3.90 |
|
1.73 |
2.75 |
|
1.29 |
2.95 |
6. In the following correlation matrix, what is the relation (number, direction, and magnitude) between…
- Pay and Satisfaction
- Stress and Health
|
Workplace |
Pay |
Satisfaction |
Stress |
Health |
|
Pay |
1.00 |
|
|
|
|
Satisfaction |
.68 |
1.00 |
|
|
|
Stress |
0.02 |
-0.23 |
1.00 |
|
|
Health |
0.05 |
0.15 |
-0.48 |
1.00 |
7. A researcher collects data from 100 people to assess whether there is any relation between level of education and levels of civic engagement. The researcher finds the following descriptive values: ̅X = 4.02, sx = 1.15, Y̅ = 15.92, sy = 5.01, SSX = 130.93, SSY = 2484.91, SP = 159.39. Test for a significant relation using the four step hypothesis testing procedure.
Answers to Odd- Numbered Exercises – Ch. 16
1. Correlations assess the linear relation between two continuous variables
5. Your scatterplot should look similar to this:
7. Step 1: H0: ρ = 0, “There is no relation between time spent studying and overall performance in class”, HA: ρ > 0, “There is a positive relation between time spent studying and overall performance in class.”
Step 2: df = 15 – 2 = 13, α = 0.05, 1-tailed test, r* = 0.441.
Step 3: Using the Sum of Products table, you should find: ̅X = 1.61, SSX = 17.44, ̅Y = 2.95, SSY =13.60, SP = 10.06, r = 0.65.
Appendix: conceptual calculations for anxiety and depression example.
We will use X for depression and Y for anxiety to keep track of our data, but be aware that this choice is arbitrary and the math will work out the same if we decided to do the opposite. Our table is thus:
|
X |
(X − ̅X) |
(X − ̅X)2 |
Y |
(Y − ̅Y) |
(Y − ̅Y)2 |
(X − ̅X)(Y − ̅Y) |
|
2.81 |
-0.35 |
0.12 |
3.54 |
-0.10 |
0.01 |
0.04 |
|
1.96 |
-1.20 |
1.44 |
3.05 |
-0.59 |
0.35 |
0.71 |
|
3.43 |
0.27 |
0.07 |
3.81 |
0.17 |
0.03 |
0.05 |
|
3.40 |
0.24 |
0.06 |
3.43 |
-0.21 |
0.04 |
-0.05 |
|
4.71 |
1.55 |
2.40 |
4.03 |
0.39 |
0.15 |
0.60 |
|
1.80 |
-1.36 |
1.85 |
3.59 |
-0.05 |
0.00 |
0.07 |
|
4.27 |
1.11 |
1.23 |
4.17 |
0.53 |
0.28 |
0.59 |
|
3.68 |
0.52 |
0.27 |
3.46 |
-0.18 |
0.03 |
-0.09 |
|
2.44 |
-0.72 |
0.52 |
3.19 |
-0.45 |
0.20 |
0.32 |
|
3.13 |
-0.03 |
0.00 |
4.12 |
0.48 |
0.23 |
-0.01 |
| total | total | total | total | total | total | total (SP) |
|
31.63 |
0.03 |
7.97 |
36.39 |
-0.01 |
1.33 |
2.22 |
The bottom row is the sum of each column. We can see from this that the sum of the X observations is 31.63, which makes the mean of the X variable ̅X = 3.16. The deviation scores for X sum to 0.03, which is very close to 0, given rounding error, so everything looks right so far. The next column is the squared deviations for X, so we can see that the sum of squares for X is SSX = 7.97. The same is true of the Y columns, with an average of ̅Y = 3.64, deviations that sum to zero within rounding error, and a sum of squares as SSY = 1.33. The final column is the product of our deviation scores (NOT of our squared deviations), which gives us a sum of products of SP = 2.22.
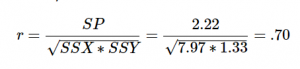
Our calculation before was r = .69, difference due to rounding issues!